Polinomi

Matlabom je vrlo jednostavno pronaći nultočke polinoma, skicirati njegov graf ili odrediti vrijednost za proizvoljan argument.
Ako želimo naći nultočke polinoma f(x)=3x4-2x3+x2-5x-7, skicirati njegov graf na području –10<x<10 te izračunati f(3+2i) pišemo:

>>f=[3 -2 1 -5 -7]

f =

3 -2 1 -5 -7

Funkcija roots traži nultočke polinoma:

>>roots(f)

ans =

1.6293
-0.0781 + 1.3303i
-0.0781 - 1.3303i
-0.8064

f(3+2i) lako izračunamo koristeći fju polyval:

>>polyval(f,3+2*i)

ans =

-3.5600e+002 +2.7000e+002i

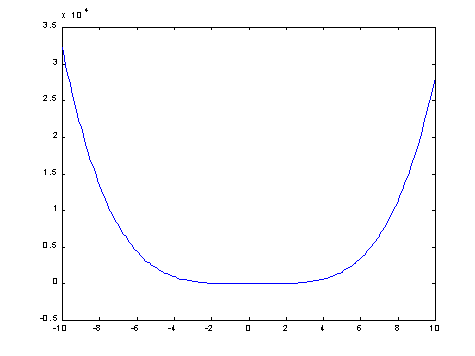
Skiciranje polinoma u rasponu –10<x<10 vršimo na slijedeći način:

>>x=-10:0.1:10;

>>plot(x,polyval(f,x))



Numeričko rješavanje sustava linearnih jednadžbi

Matlab značajno olakšava rješavanje sustava linearnih jednadžbi. Npr, potrebno je riješiti ovakav sustav linearnih jednadžbi:

4x1+9x2+2x3+4x4+6x5=6
3x1+9x2+6x3+7x4+2x5=3
8x1+7x2+3x3+2x4+8x5=8
4x2+9x3+4x4+6x5=8
7x1+4x2+7x3+9x4+1x5=5

Koeficijente uz nepoznanice unesemo u matricu A, dok članove s desne strane unesemo u vektor B. Račun se svodi na AX=B, što se formalno rješava jednostavnim dijeljenjem X=A\B.

>>A=[4 9 2 4 6
3 9 6 7 2
8 7 3 2 8
0 4 9 4 6
7 4 7 9 1];

>>B=[6 3 8 8 5]'

B =

6
3
8
8
5

>>X=A\B

X =

-0.0000
-0.4000
0
0.6000
1.2000

Dakle, vrijednosti nepoznanica su:

x1=0
x2=-0.4
x3=0
x4=0.6
x5=1.2

Zadaci

1) Naći nultočke polinoma, izračunati vrijednost za traženi x i skicirati polinom na zadanom intervalu:

a. f(x)=2x2-4x-5, f(4+4i), [0,5]
b. f(x)=3x3+2x2-x, f(-5), [-1000,1000]
c. f(x)=5x4+x2+x+2, f(-1-i), [-1,1]

2) Riješiti slijedeće sustave linearnih jednadžbi:

1.

Sustav 1:	Sustav 2:
3x1+2x2+8x3=5	8x1-3x3+5x4=2
x1+9x2+6x3=1	x2+7x4=3
x1-x2+3x3=2	4x1+12x2-2x3+2x4=-5
	2x1-3x2+4x3=5