Primjer 1. - Spremnik kao objekt vođenja
Jednostavni spremnik sa slobodnim otjecanjem ima jedan ulazni tok qu
i jedan izlazni tok qi. Cilj vođenja je najčešće
razina h tekućine u spremniku. Upravljačka varijabla je najčešće
ulazni tok qu. Sustav shematski prikazuje Sl. P.1.1.
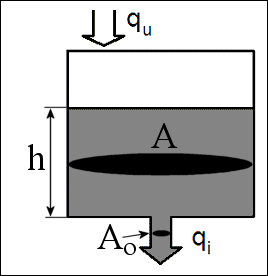
Slika P.1.1. Sustav regulacije razine vode u spremniku
Modeliranje procesa transporta fluida temelji se na zakonu o očuvanju mase:
Prirast fluida u procesnom prostoru = Ulazni tok fluida - Izlazni tok fluida
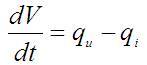
Uz konstantnost presjeka A volumen spremnika je V = A . h, pa jednadžba postaje:
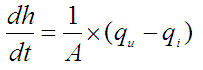
Ostaje nam još izlazni tok qi izraziti u funkciji razine h . Pri tome se koristi Toricelijeva formula koja definira brzinu slobodnog istjecanja fluida iz spremnika, samo pod utjecajem gravitacijske sile, uz zanemarivanje koeficijenata kontrakcije i koeficijenta gubitka brzine:
Ao je presjek izlazne cijevi iz spremnika. Uvrstimo li (P-1-3) u (P-1-2) i jednadžbu sredimo dobiti ćemo diferencijalnu jednadžbu koja opisuje ovisnost razine fluida u spremniku i ulaznog toka fluida u spremnik:
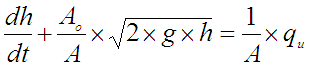
Jednadžba je nelinearna. Možemo je i linearizirati oko neke radne točke qio , ho na način da najprije prebacimo jednadžbu (P-1-3) u oblik gdje je h ovisno o qi ..
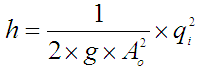
Linearizaciju provodimo tako da jednadžbu (P-1-5) zamjenjujemo linearnom
jednadžbom ![]() gdje je
gdje je 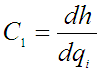 u radnoj točki qio , ho . Deriviramo
li jednadžbu (P-1-5) po qi dobijemo:
u radnoj točki qio , ho . Deriviramo
li jednadžbu (P-1-5) po qi dobijemo:
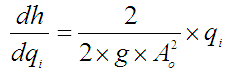
Uvrstimo li h = ho i qi= qio dobijemo:
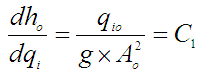
pa dalje slijedi:
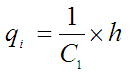
Uvrstimo li to u jednadžbu (P-1-2) dobijemo:
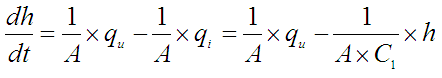
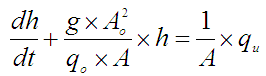
Pređemo li u s područje, uz nulte početne qio , ho uvjete dobijemo:
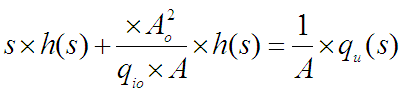
iz čega slijedi prijenosna funkcija:
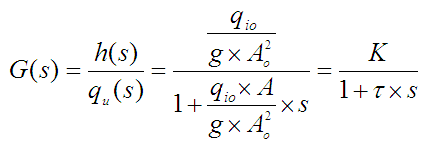
Znači linearizirani model spremnika sa slobodnim istjecanjem je prijenosna
funkcija prvog reda nulte vrsti bez nula. Vremenska konstanta
![]() punjenja spremnika upravo je proporcionalna s presjekom spremnika A
, a obrnuto proporcionalna kvadratu presjeku izlazne cijevi Ao
.
punjenja spremnika upravo je proporcionalna s presjekom spremnika A
, a obrnuto proporcionalna kvadratu presjeku izlazne cijevi Ao
.
VisSim model nelinearnog spremnika prema jednadžbi (P-1-4) prikazuje Sl.P.1.2.:
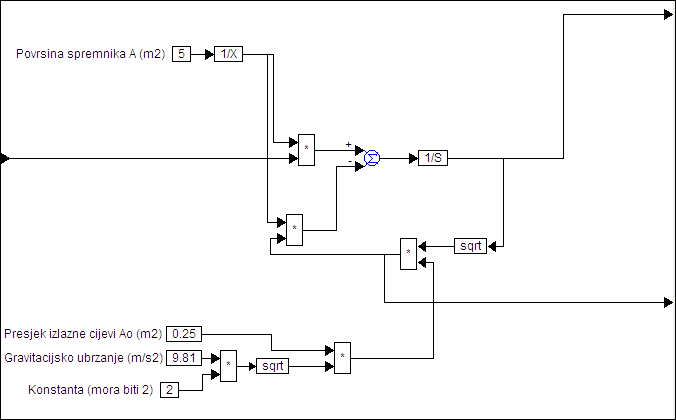
Slika P.1.2. VisSim model spremnika prema jednadžbi (P-1-4)
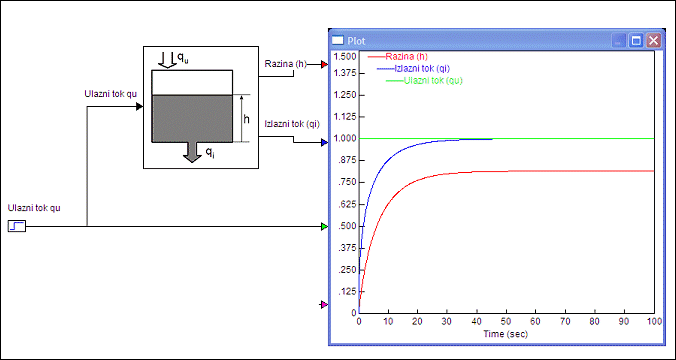
Slika P.1.3. Tipični odziv nelinearnog spremnika
Model spremnika se nalazi u datoteci vissim_primjeri.zip .
Zadatak za vježbu: Napravite linearni model spremnika prema jednadžbi (P-1-7) i usporedite da s nelinearnim modelom za različite vrijednosti ulaznog signala.
.: Slijedeća stranica > Istosmjerni motor upravljan strujom armature