Digitalno vođenje on-line (FESB, Split)

Primjer 4. - Obrnuto (invertirano) njihalo

Obrnuto njihalo na pokretnom tijelu (kolicima) je tipična aplikacija Lagrange-ovih diferencijalnih jednadžbi, koje opisuju kretanje sustava tijela spojenih na neki način zajedno. U ovaj sustav je ugrađena nelinearna ovisnost o trigonometrijskim i kvadratnim funkcijama. Kretanje sustava tijela je jednoznačno definirano pomakom kolica od neke referentne točke i kuta kojeg njihalo napravi u odnosu na vertikalu. Umjesto korištenja , može se iskoristiti horizontalni pomak y₂ ili vertikalni pomak z₂ kuglice m. Bez obzira koje se varijable koriste, važno je znati da sustav ima dva stupnja slobode i dinamika sustava mora biti opisana odgovarajućim (općim) koordinatama.

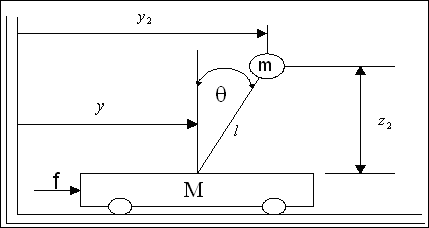
Slika P.4.1. Invertirano njihalo

Kinetička energija sustava je jednaka sumi kinetičkih energija pojedinih masa. Kolica M se mogu kretati u horizontalnom smjeru, pa je njihova kinetička energija:

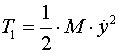
Kuglica m se može gibati u horizontalnom i vertikalnom smjeru, pa je njena kinetička energija:

;

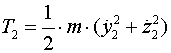
Ukupna kinetička energija sustava jednaka je:

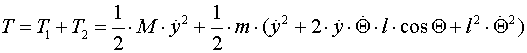
Potencijalna energija sustava jednaka je potencijalnoj energiji kuglice:

Lagranžijan je definiran kao razlika kinetičke i potencijalne energije:

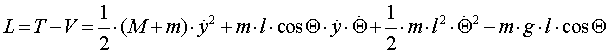
Za opće koordinate su odabrane , Lagrange-ove diferencijalne jednadžbe za ovaj sustav su:

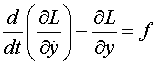
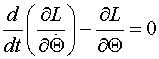
dalje slijedi:

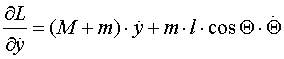
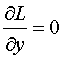
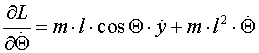
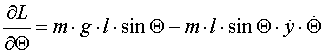
Kada se uvrste gornje jednadžbe u Lagrange-ove diferencijalne jednadžbe dobiju se jednadžbe koje opisuju kretanje obrnutog njihala na kolicima:

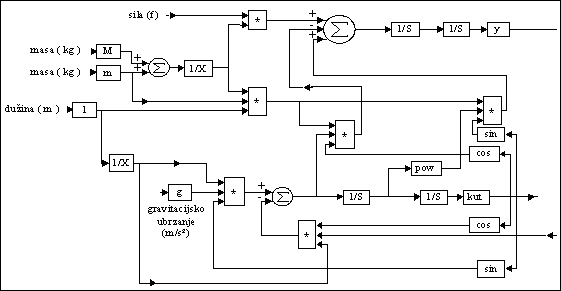
Iz ovih jednadžbi je modeliran sustav u VisSim-u prikazan na slijedećoj slici:

Slika P.4.2. VisSim model invertiranog njihala

Rezultati simulacije prikazani su na sljedećoj slici:

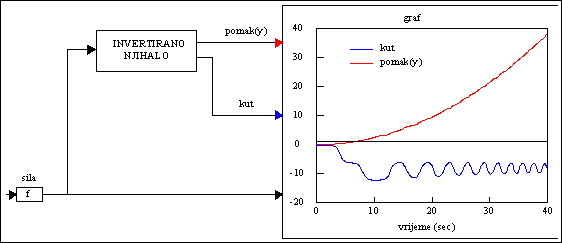
Slika P.4.3. Vremenska promjena kuta i pomaka y

Podaci za ovu simulaciju su:

; ; ; ; ; "step size" ; primijenjena je numerička metoda integriranja Runge Kutta 2nd order.

Da bi se ocijenio utjecaj izabranog vremena uzorkovanja na rezultate simulacije, provodi se simulacija za nekoliko različitih vrijednosti vremena uzorkovanja , uz iste ostale parametre modela. Rezultati te simulacije prikazani su na slijedećoj slici:

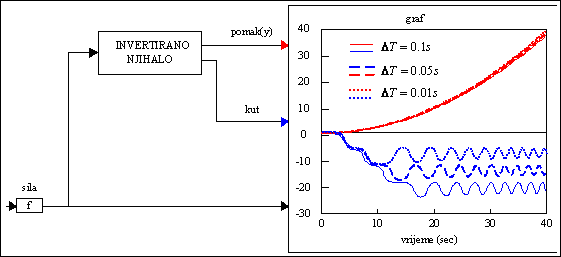
Slika P.4.4. Utjecaj izabranog vremena uzorkovanja na rezultate simulacije

Podaci za ovu simulaciju su:

; ; ; ; ; "step size" u prvom slučaju je , drugom i trećem ; primijenjena je numerička metoda integriranja Runge Kutta 2nd order.

Ako se za iste parametre modela i isto vrijeme uzorkovanja , mijenjaju numeričke metode integriranja, može se vidjeti utjecaj različitih numeričkih metoda integriranja na rezultate simulacije:

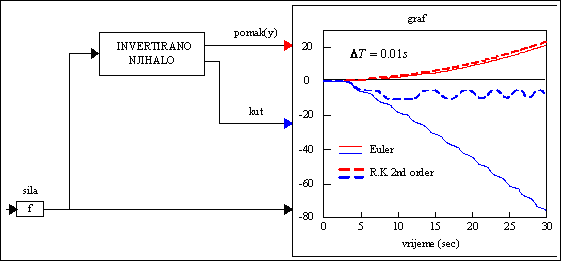
Slika P.4.5. Utjecaj različitih numeričkih metoda integriranja na izgled krivulja

Podaci za ovu simulaciju su:

; ; ; ; ; , primijenjene su dvije numeričke metode integriranja Euler-ova metoda i Runge Kutta 2nd order (te metode se nalaze u "simulation setup").

Prethodni slučaj je ponovljen za drugo vrijeme uzorkovanja , rezultati simulacije prikazani su na sljedećoj slici:

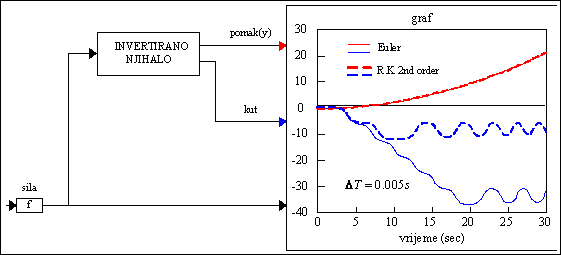
Slika P.4.6. Utjecaj različitih numeričkih metoda integriranja na izgled krivulja

Podaci za ovu simulaciju su:

; ; ; ; ; , primijenjene su dvije numeričke metode integriranja Euler-ova metoda i Runge Kutta 2nd order.

Model obrnutog njihala se nalazi u datoteci vissim_primjeri.zip.

.: Slijedeća stranica > Spremnici u slijedu (neinteraktivni sustav spremnika)