Primjer 5. - Spremnici u slijedu (neinteraktivni sustav spremnika)
Neinteraktivni sustav spremnika je primjer za serijske sustave, i prikazan je na slijedećoj slici.
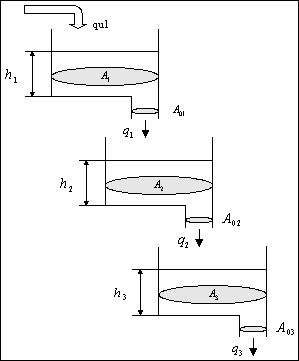
Slika P.5.1. Neinteraktivni sustav spremnika
Opći oblik jednadžbe koja opisuje ovakav sustav je:
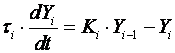 za i=1,2,…,n
Y0 = X
za i=1,2,…,n
Y0 = X
Svaki sustav modeliran iz jednadžbe ovakvog oblika predstavlja neinteraktivni serijski sustav. U jednadžbi se pojavljuju samo oblici Yn-1 i Yn (nema Yn+1) iz čega slijedi da spremnik koji se nalazi nizvodno (npr. spremnik 2) nema utjecaja na spremnik koji se nalazi uzvodno (spremnik 1).
Opća neinteraktivna serija sustava prvog reda može se razviti primjenjujući Laplace-ovu transformaciju na svaku jednadžbu koja slijedi iz jednadžbe (23) i kombiniranjem sa izrazima za jedan ulaz-izlaz. Svaka serija je predstavljena odgovarajućom prijenosnom funkcijom Gi(s), pa je prijenosna funkcija cijelog sustava:
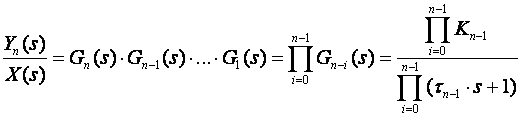
gdje je Kn-1 pojačanje svakog pojedinačnog sustava prvog reda, a tn-1 je vremenske konstanta pojedinog sustava prvog reda.

Slika P.5.2. Serijski sustav
Npr. za 3 spremnika, diferencijalne jednadžbe glase:
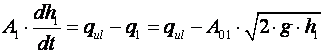

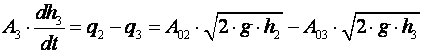
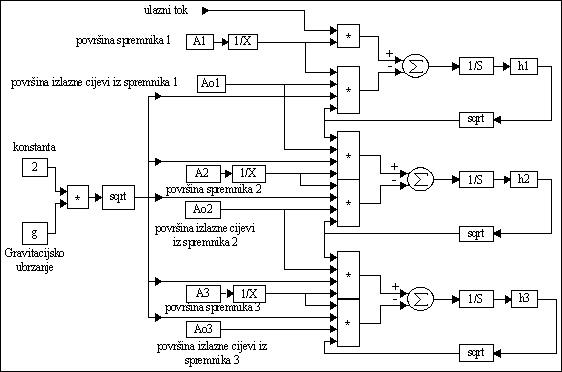
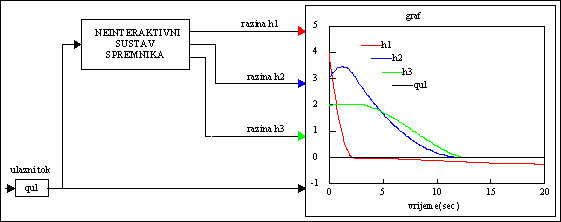
Slika P.5.3. VisSim model neinteraktivnog sustava spremnika
Rezultati provedene simulacije prikazani su na sljedećoj slici:
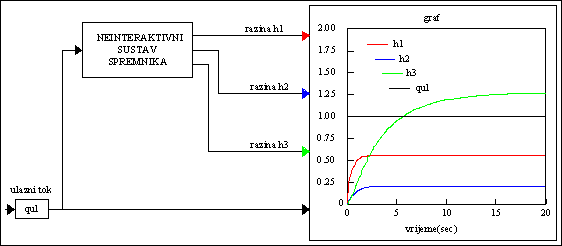
Slika P.5.4. Vremenska promjena razina h1, h2
i h3
Podaci za simulaciju su:
;
;
;
;
;
;
;
; primijenjena je numerička metoda integriranja Runge Kutta 2nd order.
U spremnicima mogu postojati početne vrijednosti razina h10,
h20, h30 (koje se
namještaju kao početna stanja integratora u blok shemi). Rezultati
simulacije sa početnim vrijednostima razina prikazani su na sljedećoj
slici:
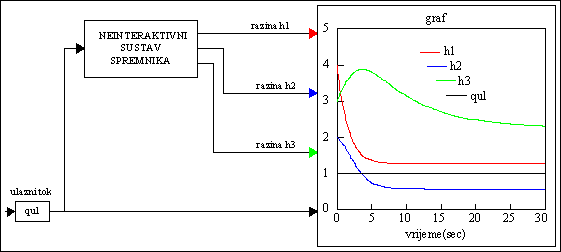
Slika P.5.5. Vremenska promjena razina h1, h2 i
h3 (kada postoje h10, h20,
h30)
Podaci za simulaciju su:
;
;
;
;
;
;
;
; početne vrijednosti razina su:
,
,
; primijenjena je numerička metoda integriranja Runge Kutta 2nd order.
Sustav neinteraktivno spojenih spremnika je primjer viševeličinskog
sustava (MIMO) sa karakteristikama sustava 1. reda. Simulacijski su
zaključci kao kod Promjera 1. (tj. vrijeme uzorkovanja
![]() ne utječe značajno
na prikaz karakterističnog vladanja sustava) uz dodatni zaključak, da
dobra simulacija može upozoriti na nepromišljene fizikalne pretpostavke.
Simulacija alarmira da je fizikalno nemoguće sustav uvesti u
pretpostavljene radne uvjete (prazna posuda iz koje izlazi tekućina).
ne utječe značajno
na prikaz karakterističnog vladanja sustava) uz dodatni zaključak, da
dobra simulacija može upozoriti na nepromišljene fizikalne pretpostavke.
Simulacija alarmira da je fizikalno nemoguće sustav uvesti u
pretpostavljene radne uvjete (prazna posuda iz koje izlazi tekućina).
Prilikom izvođenja simulacija za različite vrijednosti parametara, pojavljuju se situacije koje su u stvarnosti nemoguće, pa VisSim zaustavlja simulaciju u tom trenutku (nude se tri opcije, prva je prekid simulacije u tom trenutku tj."Abort", druge dvije nude nastavak simulacije, iako je rezultat fizički nemoguć. Te druge dvije opcije su "Retry" i "Ignore"). Sljedeća simulacija prikazuje jedan takav slučaj:
Slika P.5.6. Prikaz nerealne situacije kada razina h1
poprima negativnu vrijednost
Podaci za simulaciju su:
;
;
;
;
;
;
;
; početne vrijednosti razina su:
,
,
; primijenjena je numerička metoda integriranja Runge Kutta 2nd order.
U trenutku t=2.255s simulacija je zaustavljena zbog pojave negativnog
argumenta u korijenu diferencijalne jednadžbe (VisSim to javlja kao
"negative arg to sqrt" i promjeni boju bloka kod kojeg je došlo do te
situacije), to je trenutak kada razina h1 dostiže vrijednost nula i ulazi u
negativnu vrijednost. Simulacija se može nastaviti odabirom odgovarajuće
opcije, ali se na slici zapaža pojava negativne vrijednosti razine h1 što je
u stvarnosti nemoguće.
Još jedan primjer koji daje nerealne rezultate prikazan je na slijedećoj slici:

Slika P.5.7. Prikaz nerealne situacije kada razina h2 poprima negativnu vrijednost
Podaci za simulaciju su:
;
;
;
;
;
;
;
; početne vrijednosti razina su:
,
,
; primijenjena je numerička metoda integriranja Runge Kutta 2nd order.
Kod ovog primjera postoji ulazni tok, ali je nakon t=1.95s simulacija
zaustavljena jer tada razina h2 ulazi u negativnu vrijednost što je nemoguće.
Model
neinteraktivnog sustava spremnika se nalazi u datoteci vissim_primjeri.zip.
.: Slijedeća stranica > Spregnuti spremnici (interaktivni sustav spremnika)