Primjer 7. - Dvoosovinsko vozilo
Matematički model kod pravocrtnog gibanja vozila
Da bi se vozilo pokrenulo potrebno je savladati otpore vožnje i ubrzavanja. Zbog jednostavnosti proračuna u ovom zadatku uzima se da je upravljački signal, tj. akceleracija (deceleracija) a konstantna u vremenu gibanja.
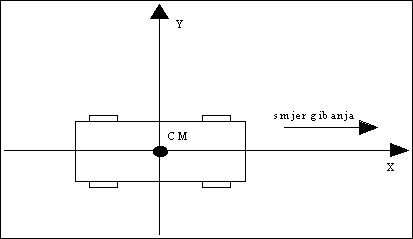
Slika P.7.1. Prikaz vozila u koordinatnom sustavu
Ako ne postoji zakret prednjih kotača vozilo se giba pravocrtno u pozitivnom smjeru osi X, diferencijalna jednadžba koja opisuje takvo gibanje glasi:
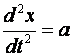
Rješavanjem ove diferencijalne jednadžbe dobiju se slijedeće relacije:
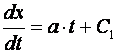
u trenutku
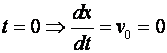
(pretpostavka je da u početnom trenutku vozilo miruje)
![]()
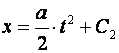
u trenutku
![]()
VisSim model pravocrtnog gibanja vozila prikazan je na slijedećoj slici:
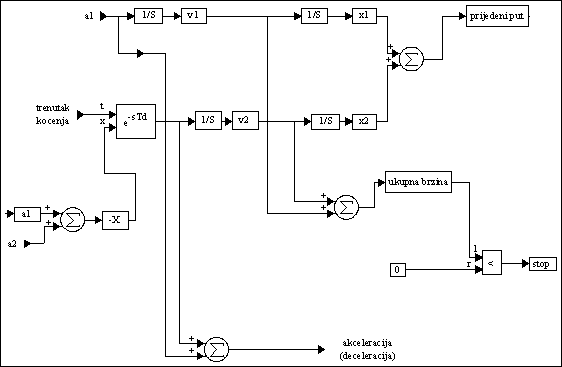
Slika P.7.2. VisSim model pravocrtnog gibanja vozila
Rezultati simulacije prikazani su na sljedećoj slici:
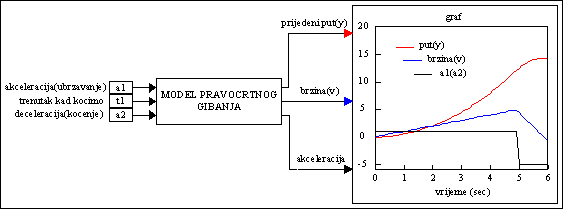
Slika P.7.3. Vremenska promjena puta y, brzine v i
upravljačkog signala a1(a2)
Podaci za provedenu simulaciju su:
;
;
; "step size"
; primijenjena je numerička metoda integriranja Runge Kutta 2nd order.
Upravljački signali u simulaciji su akceleracija a1 i deceleracija
(kočenje) a2, upravljački signal promjeni samo jednom svoj predznak u
simulaciji, i to u trenutku t1 (trenutak kočenja). Vozilo ubrzava do
trenutka kočenja t1, a ostalo vrijeme (dok se ne zaustavi) usporava.
Fazna krivulja koja prikazuje ovisnost brzine o prijeđenom putu, prikazana je na slijedećoj slici:
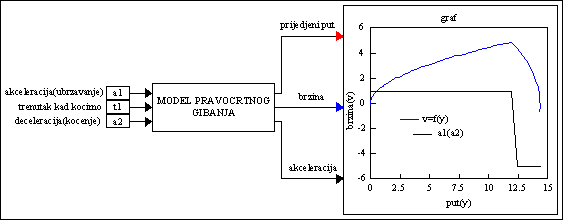
Slika P.7.4. Fazna krivulja
![]()
Iz fazne krivulje može se zaključiti na vrijeme t1 kada auto počinje usporavati, tj. kako se odnose brzina i put prije i poslije tog trenutka. (Faznu krivulju se dobije ako se otvori "plot setup" i označi opcija "XY Plot" i u "X Axsis" broj 1(točkom), te se odvoji ulaz "akceleracija(deceleracija) " sa "Plot" bloka.)
Model
pravocrtnog gibanja vozila se nalazi u datoteci vissim_primjeri.zip.
.: Slijedeća stranica > Model vozila koje se giba po kružnici