A-1 Neki pojmovi matrične algebre

-------------------------------------------------------------------------------

Pozitivno definitna i pozitivno semidefinitna matrica

Simetrična matrica A (m x m) je pozitivno definitna ukoliko za bilo koji netrivijalni vektor x (x ≠ 0) vrijedi

  > 0          (A.1.1)

To povlači svojstvo da postoji linearna transformacija  y=T x  takva da je

         (A.1.2)

Ukoliko vrijedi

      (A.1.3)

matrica je pozitivno semidefinitna (nenegativno definitna). Za pozitivno semidefinitne matrice vrijedi svojstvo da postoji linearna transformacija  y=T x  takva da je

      (A.1.4)

Primjer:

Matrica 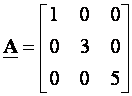je pozitivno definitna zato što za bilo koji vektor 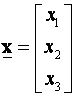različit od nule (x ≠ 0) vrijedi > 0.

Matrica 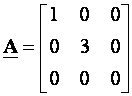je pozitivno semidefinitna (u izrazu nema trećeg člana pa za vektor 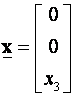p može biti jednak 0.

Pozitivna definitnost može se utvrditi korištenjem Sylvesterovog kriterija koji kaže da će matrica reda nxn biti pozitivno definitna ukoliko su joj sve vrijednosti glavnih subdeterminanti (minora) pozitivne. Glavne subdeterminante formiraju se tako da se prvi element uzme za  subdeterminantu reda 1x1 i zatim se povećava red dodavanjem elemenata koji okružuju tu subdeterminantu sa desne strane i ispod nje. Zadnja glavna subdeterminanta je determinanta cijele matrice.

Za gornji primjer imamo

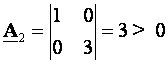
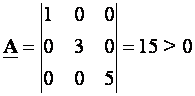
pa je matrica pozitivno definitna što smo i utvrdili.

-------------------------------------------------------------------------------

Trag matrice A koji označavamo tr (A) je suma dijagonalnih elemenata matrice A

Primjer

-------------------------------------------------------------------------------

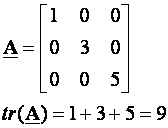
Inverzija matrice A je matrica A^-1 koja zadovoljava matričnu jednadžbu A A^-1= I

Računa se izrazom

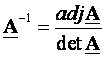
gdje je det A determinanta matrice  A, a adj A je transponirano-recipročna (adjungirana) matrica matrice A. Adjungiranu matricu matrice A za slučaj realnih matrica računamo tako da transponiramo recipročnu matricu A* matrice  A.

Recipročna matrica A*jest matrica kofaktora [a_ij] matrice A.

Kofaktor a_ij matrice A jednak je subdeterminanti D_ij matrice koja ostane kad se u matrici A prekriži i-ti redak i j-ti stupac pomnoženoj s faktorom (-1)^i+j:

Primjer:

Invertirajmo matricu iz Poglavlja 3.5.4 – text_3-23.htm

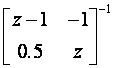
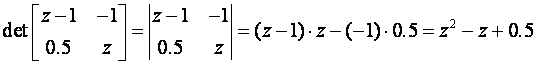
Recipročna matrica je

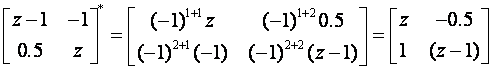
a adjungirana matrica je

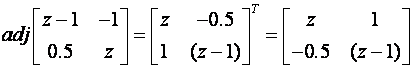
pa je inverzna matrica

-------------------------------------------------------------------------------

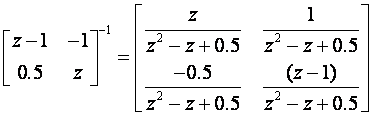
Matrica< A je singularna ako joj je determinanta jednaka 0. Singularna matrica nema inverzne matrice.

-------------------------------------------------------------------------------

Rang matrice A  jednak je maksimalnom broju linearno nezavisnih stupaca matrice. Računa se preko subdeterminanti i odgovara redu najveće subdeterminante različite od nule. Uvijek se kreće od subdeterminante najmanjeg reda. Ukoliko nađemo subdeterminantu reda k koja je različita od nule a aubdeterminanta reda (k+1) je jednaka nuli matrica ima rang k. Matematički se postupak svodi na formiranje dijagonalne matrice. Rang matrice je jednak broju dijagonalnih elemenata u gornjem lijevom uglu različitih od nule.

Primjer

 

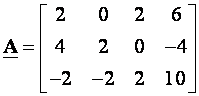
Kako postoji submatrica trećeg reda jednaka nuli

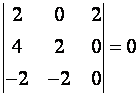
matrica ima rang 2

-------------------------------------------------------------------------------

  Vlastite vrijednosti i vlastiti vektor matrice. Neka je A realna matrica n-tog reda. Realni broj λ zove se vlastita vrijednost (ili karakteristična) matrice A i piše se λ=eig(A) onda i samo onda ukoliko postoji vektor x takav da zadovoljava jednadžbu:

x se naziva vlastiti vektor matrice  A koji pripada vlastitoj vrijednosti λ.

Jednadžba će imati netrivijalno rješenje samo u slučaju ukoliko je karakteristična jednadžba matrice A jednaka nuli:

Rješenja karakteristične jednadžbe

ujedno su i vlastite vrijednosti matrice A :

Primjer:

Neka je

Karakteristična jednadžba je:

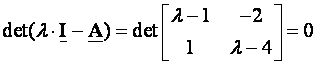
iz čega slijedi:

Rješenja jednadžbe su:

a to su ujedno i vlastite vrijednosti matrice  A:

Vlastite vektore dobijemo iz jednadžbi:

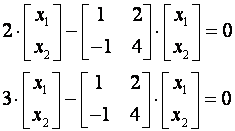
pa je za vlastiti vektor , a za vlasti vektor je .

-------------------------------------------------------------------------------

Cayley-Hamiltonov teorem kaže da svaka kvadratna matrica zadovoljava svoju karakterističnu jednadžbu.

Primjer:

Karakteristična jednadžba matrice

je  .

Formiramo li matričnu jednadžbu

i izračunamo li je vidjeti ćemo da će biti zadovoljena.

-------------------------------------------------------------------------------

Norma vektora

Norma vektora x = [x₁ x₁ ^... x_n]^T koju označavamo || x || definira se pozitivnim korijenom produkta x^Tx :

 

i računa jednadžbom

-------------------------------------------------------------------------------

 

U slijedećem poglavlju prisjećamo se kako se specifikacije definiraju u vremenskom području.

.: Slijedeća stranica > Specifikacija odziva u vremenskom području i s-ravnini