5.  Projektiranje diskretnih regulatora

Napokon smo došli i do onoga zbog čega sve ovo sve učimo – do projektiranja digitalnog vođenja, projektiranja digitalnog regulatora koji će 'natjerati' regulacijski sustav da se ponaša upravo onako kako mi to želimo. Naglasimo odmah na početku: Iako je krajnja realizacija digitalni regulator, mi  u stvari projektiramo diskretni regulator. Svi postupci sinteze koji će se spomenuti u ovom poglavlju odnose se na diskretni regulator i regulacijsku shemu prikazanu slikom 5.1.

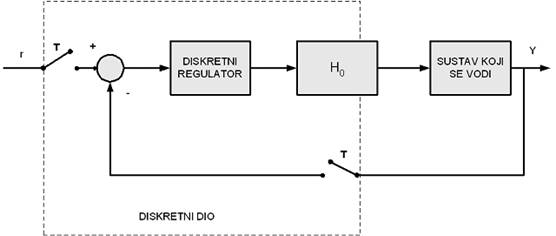
Slika 5.1. Ekvivalentna shema diskretnog sustava vođenja

a konačna realizacija će biti u obliku sheme na slici 5.2.

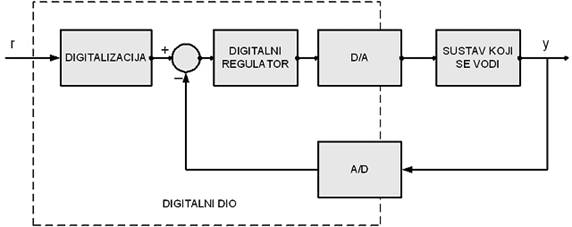
Slika 5.2. Stvarna izvedba sustava digitalnog vođenja

O tome smo već govorili u poglavlju 2.4. Digitalni regulator bit će u stvari program digitalnog računala kojim modeliramo ponašanje projektiranog diskretnog regulatora. U poglavlju 6 o realizaciji digitalnog vođenja osvrnut ćemo se i na probleme koje se javljaju prelaskom iz diskretnog oblika u oblik pogodan za primjenu na digitalnom računalu.

U poglavlju 1.2.2. Sustav vođenja kazali smo da su osnovni elementi procesa koji nazivamo vođenje:

- ciljevi vođenja (Z* ),

- informacije o stanju okoline i objekta (I),

- algoritam vođenja ( ),

- signal vođenja (U_o).

Izostanak bilo kojeg od ovih faktora čini vođenje nemogućim. Ono što nas u ovom poglavlju zanima je algoritam vođenja. Kako odrediti algoritam uz pomoć kojega će sustav koji se vodi zadovoljiti ciljeve vođenja? Uobičajeno je da se algoritam vođenja iskazuje u matematičkom obliku, a ciljevi vođenja u obliku specifikacija koje vođeni sustav treba zadovoljavati. Matematički opis algoritma vođenja u diskretnom području može biti ili impulsna prijenosna funkcija diskretnog regulatora ili opis diskretnog regulatora varijablama stanja. (Napomena: U poglavlju 5.6 u kojem ćemo govoriti o postupcima temeljenim na računalnoj inteligenciji algoritam vođenja je moguće definirati i na neke drugačije načine, ali se za sada zadržimo na ovim uobičajenim načinima opisa diskretnog regulatora).

Nakon što se odredi matematički opis diskretnog regulatora slijedi njegova realizacija koja se svodi na pretvorbu matematičkog opisa regulatora u oblik pogodan za programiranje. To je najčešće oblik jednadžbe diferencija gdje se diskretna vrijednost upravljanja u(kT) u svakom diskretnom trenutku kT iskazuje kao u ovisnosti o sadašnjoj vrijednosti pogreške e(kT), prošlim vrijednostima pogreške e[(k-1)T], e[(k-2)T], ... , i prošlim vrijednostima upravljačkog signala u[(k-1)T], u[(k-2)T], .... Nakon implementacije na digitalnom računalu, diskretni regulator postaje digitalni regulator.

Znači cijeli postupak projektiranja digitalnog regulatora sastoji se od sljedećih koraka:

a) Definiranje specifikacija na temelju postavljenih ciljeva vođenja;

b) Proračun matematičkog oblika diskretnog regulatora koji će te specifikacije zadovoljiti bilo u obliku impulsne prijenosne funkcije bilo u obliku matematičkog opisa varijablama stanja;

c) Realizacija diskretnog regulatora koja se svodi na izvođenje jednadžbe diferencija koja opisuje ponašanje regulatora i na kraju

d) Implementacija diskretnog regulatora pisanjem programa za digitalno računalo u nekom od programskih jezika.

U ovom se poglavlju prvenstveno bavimo točkom b) i c), ali kako se svaki postupak projektiranja oslanja na neke od specifikacija neizbježno je da i njih stalno spominjemo. Specifikacije se mogu postaviti u vremenskom, frekvencijskom i kompleksnom području, a sve u biti definiraju ponašanje sustava u vremenu. Nas na kraju uvijek zanima kako će se vođeni sustav ponašati u vremenu. Hoće li on, ukoliko se radi o zadatku stabilizacije, održavati izlaznu vrijednost na postavljenoj razini, ili ukoliko se radi o servo zadatku, hoće li izlazna veličina na zadovoljavajući način pratiti promjene referentne veličine. U Dodatku A – Definicije navedene su sve osnovne specifikacije vremenskog, frekvencijskog i kompleksnog područja. Korisno ih je pročitati prije nastavka izučavanja metoda projektiranja diskretnog regulatora.

Diskretni se regulator može u osnovi projektirati na dva načina. Obično se polazi od matematičkog modela sustava koji se vodi, a koji može biti iskazan u obliku prijenosne funkcije G(s) ili u obliku jednadžbi varijabli stanja. Zadržimo se za sada na tome da je sustav modeliran prijenosnom funkcijom G(s). Postupci kojima možemo doći do diskretnog regulatora su:

a) Sinteza regulatora u kontinuiranom području: Cijeli proračun regulatora provodimo u kontinuiranom području i tek na kraju, kada je regulator u potpunosti definiran i opisan prijenosnom funkcijom G_C(s), prelazimo u diskretno područje. Postupak se zove diskretizacija kontinuiranih regulatora. Kod njega je proračun regulatora u kontinuiranom području, a realizacija regulatora u diskretnom području.

b) Sinteza regulatora u diskretnom području: Odmah se prebaciti u diskretno područje na način da odredimo diskretni ekvivalent prijenosne funkcije sustava koji se vodi. Do njega dolazimo primjenom nekog od postupaka o kojima smo govorili u poglavlju 3.4.2: primjena Z transformacije na ekvivalentni sustav (serijski spoj sklopa za obnavljanje i našeg kontinuiranog sustava), aproksimacijski postupci ili postupci poklapanja polova i nula. Nakon toga se proračun regulatora G_C(z) provodi u diskretnom području. Parafrazirajući pojam direktnog digitalnog vođenja (eng. DDC - Direct Digital Control) ovaj bi postupak mogli nazvati direktna digitalna sinteza (eng. DDS - Direct Digital Synthesis). Varijanta ovog postupka je da se na temelju odziva sustava odmah izgradi diskretni model bez traženja kontinuirane prijenosne funkcije vođenog sustava. Nazivamo je sinteza diskretnog regulatora na temelju diskretnog modeliranja sustava koji se vodi. Ima dvije varijante. Kod jedne se sinteza temelji na impulsnoj prijenosnoj funkciji kontinuiranog sustava dobivenoj eksperimentalnom identifikacijom.  O njoj smo govorili u poglavlju 3.4.4 koje se zove Parametarska identifikacija impulsne prijenosne funkcije. Kod druge se uzimaju diskretne vrijednosti odziva na skokovitu pobudu, a diskretni regulator se računa u obliku regulatora po varijablama stanja.

c) Sinteza regulatora u pseudo-frekvencijskom w području: To je varijanta postupka projektiranja regulatora koja na neki način kombinira oba prije spomenuta postupka. Sastoji se u tome da se model vođenog sustava prikaže diskretnim ekvivalentom, pa da se nakon toga na njega primjeni još jedna transformacija, ovaj put bilinearna  te se on prebaci u w područje. Regulator se tu i proračuna koristeći na primjer Bodeove dijagrame, a konačni oblik regulatora se dobije vraćanjem natrag iz G_C(w) u G_C(z). Cijela je ova procedura slična vožnji iz Splita u Šibenik preko Knina i Drniša. Postavlja se pitanje ima li je smisla koristiti ukoliko smo u diskretno područje došli diskretizacijom kontinuiranog sustava koji se vodi. Sintezu temeljenu na Bodeovim dijagramima mogli smo odmah provesti  u kontinuiranom području. U w području javljaju se dodatni problemi, na primjer frekvencije nam potpuno ne odgovaraju onima iz s područja (zato ih i zovemo pseudo-frekvencije). Međutim ukoliko smo u diskretno područje došli direktno, bez izvođenja kontinuirane prijenosne funkcije, postupak ima smisla. Iz z područja se ne može jednoznačno preći u s područje, ali primjena bilinearne transformacije daje jednoznačno preslikavanje. Postupci sinteze koji se na primjer temelje na Bodeovim dijagramima su izuzetno dobro razrađeni i daju intuitivni uvid u frekvencijske karakteristike budućeg sustava, a posebno u mjere relativne stabilnosti. Postupci su skoro identični onima iz kontinuiranog područja pa ćemo ih samo spomenuti u Poglavlju o projektiranju regulatora u pseudo-frekvencijskom w području. Više ćemo pažnje posvetiti postupcima specifičnim za diskretno područje.

Kod diskretizacije kontinuiranih regulatora možemo primijeniti:

a) postupak ekvivalentnog regulatora,

b) postupak diskretnog ekvivalenta, i

c) postupak poklapanja polova i nula.

Posebno mjesto u svemu tome zauzima diskretizacija PID regulatora koji je sigurno u primjeni najčešći od svih regulatora.

Kod direktne digitalne sinteze tri su moguća pristupa:

a) Analizom polova impulsne prijenosne funkcije sustava koji se vodi i željenog položaja polova budućeg zatvorenog regulacijskog sustava (do kojih smo došli na temelju postavljenih specifikacija na odziv vođenog sustava) polova i nula regulatora postavljaju se točno na mjesta gdje bi trebali biti da se sustav ponaša onako kako želimo. Kako se postupak obično provodi crtajući GMK diskretiziranog sustava zovemo ga postupak postavljanja polova i nula regulatora temeljen na GMK (geometrijskom mjestu korijena).

b) I drugi se pristup temelji na postavljanju polova regulatora samo što ih ovaj put postavljamo tako da najprije definiramo željeno ponašanje sustava definirajući željenu prijenosnu funkciju zatvorenog sustava Y(z)/R(z). Zovemo ga postupak temeljen na postavljanju polova (i nula) regulatora i definiranju željenog modela vođenog sustava. Postupak ćemo ilustrirati primjerom Dahlinovog regulatora.

c) Treći se postupak razlikuje samo u tome što željeno ponašanje vođenog zatvorenog sustava definiramo željenim odzivom u diskretnim trenucima vremena. On se u stvari jedini u potpunosti odvija u diskretnom području. Nakon određivanja diskretnog ekvivalenta kontinuiranog dijela sustava ostatak postupka se odvija isključivo u diskretnom području. Zovemo ga postupak temeljen na definiranju željenog odziva zatvorenog regulacijskog sustava u diskretnim trenucima vremena. Primjeri regulatora proračunatih ovim postupkom su tzv. 'deadbeat' regulator i Kalmanov regulator.

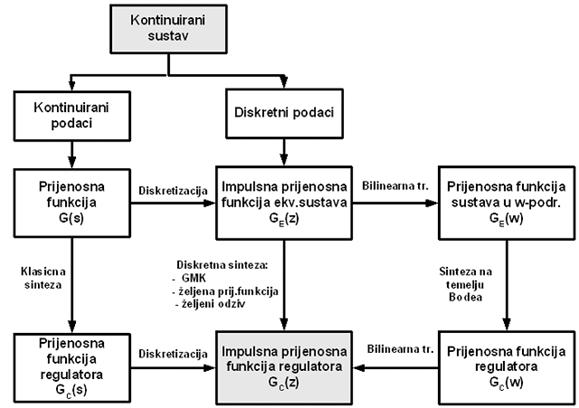
Slika 5.3 pregledno prikazuje sve postupke sinteze diskretnog regulatora koje smo spomenuli.

Slika 5.3. Postupci projektiranja diskretnog regulatora temeljeni na prijenosnoj funkciji sustava koji se vodi

Sve metode na kraju daju isto – impulsnu prijenosnu funkciju regulatora

                (5.1)

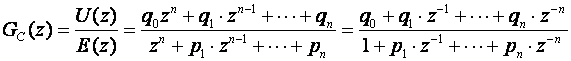
koju u vremenskom području prebacujemo u jednadžbu diferencija koja daje upravljanje u diskretnom trenutku kT:

          (5.2)

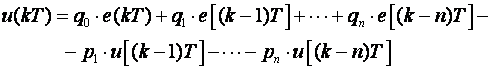
Razlikuju se jedino vrijednosti koeficijenata (koji naravno mogu biti i jednaki 0). Njihove vrijednosti prije svega ovise o postavljenim specifikacijama, ali i o postupku proračuna algoritma vođenja. Postupak prebacivanja impulsne prijenosne funkcije u jednadžbu diferencija naziva se realizacija diskretnog regulatora i izučava se u 6. poglavlju.

Svi ovi do sada spomenuti postupci temelje se na povratnoj vezi po izlazu. U engleskom govornom području postupci projektiranja vođenja koji se temelje na povratnoj vezi po izlazu uobičajeno se nazivaju Output Feedback (OPFB) Design Methods. S druge strane postoji cijeli niz postupaka koji se temelje na povratnoj vezi po varijablama stanja.  Poznavanje stanja sustava otvara mogućnosti koje regulatorom temeljenim na povratnoj vezi po izlazu nije moguće napraviti. Zbog toga smo ovim postupcima posvetili posebno poglavlje o projektiranju diskretnog regulatora temeljeno na povratnoj vezi po varijablama stanja. U engleskom govornom području postupci projektiranja vođenja koji se temelje na povratnoj vezi po varijablama stanja uobičajeno se nazivaju  State Variable Feedback  (SVFB) Design Methods.

Na kraju je dan kratki pregled postupaka vođenja temeljen na računalnoj inteligenciji. Kako se 'inteligentni' regulatori realiziraju na digitalnom računalu uvrstili smo kratki opis i tih postupaka, iako oni po svom značaju zahtijevaju cijeli on-line tutorijal.

U nastavku se nećemo baviti najprije zadacima projektiranja regulatora u kontinuiranom području. Pretpostaviti ćemo da je regulator proračunat, da je poznata njegova prijenosna funkcija ili diferencijalna jednadžba, te da ga je sada iz kontinuiranog područja potrebno prebaciti u diskretno. Posebno ćemo govoriti o problemu diskretizacije PID (proporcionalno – integracijsko – derivacijskog) regulatora. Kazati ćemo nešto i o heurističkom podešavanju njegovih parametara.

U poglavlju iza toga slijede temelji projektiranja regulatora u diskretnom području. Početi ćemo s projektiranjem regulatora korištenjem geometrijskom mjestu korijena diskretnog sustava, te nastaviti s algoritmima temeljenim na željenoj prijenosnoj funkciji te na  karakteristikama odziva zatvorenog regulacijskog sustava.

Svi se ovi postupci temelje na impulsnoj prijenosnoj funkciji vođenog sustava. Kako se sustav može opisati i jednadžbama varijabli stanja to otvara cijelo jedno novo područje projektiranja diskretnog regulatora temeljeno na povratnoj vezi po varijablama stanja.

Na kraju slijedi kratki pregled postupaka vođenja temeljenog na računalnoj inteligenciji, prije svega na umjetnim neuralnim mrežama i neizrazitim (fuzzy) skupovima. Uvrstili smo ih u digitalno vođenje zato što se ti postupci u biti jedino i implementiraju uz pomoć digitalnog računala.

.: Sljedeća stranica > Diskretizacija kontinuiranih regulatora