2.4. Digitalni sustav vođenja i njegovo modeliranje
Ponovimo li spoznaje iz poglavlja 2.2. i 2.3, postupak pretvorbe analognog, kontinuiranog signala u digitalni i obrnuto možemo prikazati slikama 2.4.1 i 2.4.2. Kod analogno - digitalne pretvorbe četiri su temeljna postupka: uzorkovanje, amplitudna kvantizacija, rekonstrukcija 0-tog reda i digitalno kodiranje.
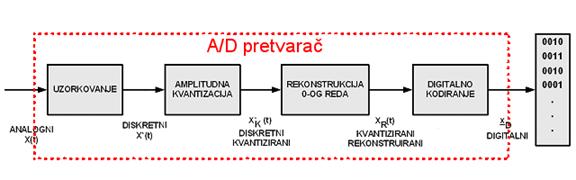
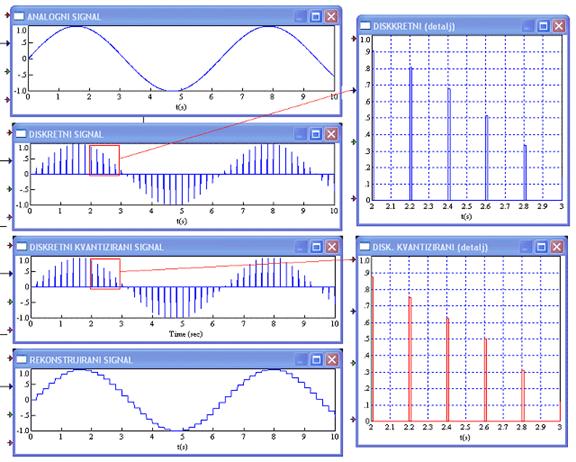
Slika 2.4.1. Pretvorba analognog u digitalni signal (cijeli se postupak događa u A/D pretvaraču) (digitalizacija.vsm)
Kod povećanog diskretnog i diskretnog kvantiziranog signala lako je uočiti razlike u vrijednostima diskretnog signala. Kvantizacija je 4-bitna (16 razina). Kod digitalno - analognog pretvarača postupak je suprotan. Digitalni se signal pretvara u diskretni (fiktivno) a nakon toga se iz njega formira kontinuirani tako da se između dva perioda uzorkovanja zadrži početna vrijednost.
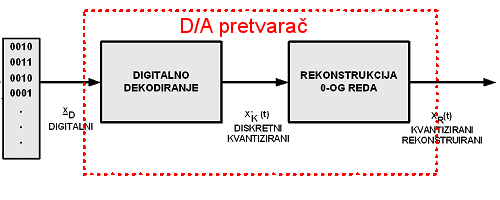
Slika 2.4.2. Pretvorba digitalnog u analogni signal
Povežemo li sve zajedno u sustav vođenja dolazimo do osnovne sheme sustava digitalnog vođenja s negativnom povratnom vezom (slika 2.4.3).
Slika 2.4.3. Sustav digitalnog vođenja s negativnom povratnom vezom
Sustav ima digitalni dio i analogni dio. Kod analize ovakvih sustava postupak digitalnog kodiranja i dekodiranja najčešće se ne uzima u razmatranje, pa se A/D pretvarač promatra isključivo kao sklop za uzimanje uzoraka, a D/A pretvarač kao sklop za obnavljanje 0-tog reda, dok se digitalni regulator promatra kao diskretni regulator i predstavlja impulsnom prijenosnom funkcijom GC(z) koju obrađujemo u poglavlju 3.4. (slika 2.4.4).
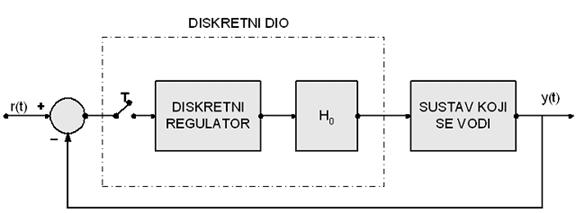
Slika 2.4.4. Sustav digitalnog vođenja prikazan samo svojim diskretnim ekvivalentom
Napomena:
U praktičnim primjenama komparator se obično uključuje u digitalni dio (još jedna linija koda), a digitalizira se izlazna veličina y(t) pomoću A/D pretvarača i referentna veličina direktnim unosom brojčane (digitalne) vrijednosti preko tastature.
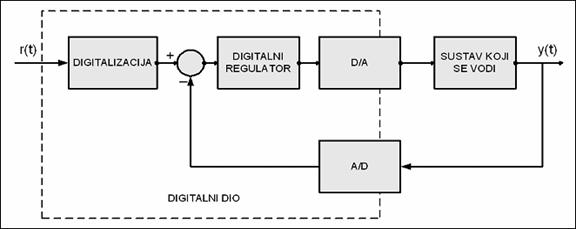
Slika 2.4.5 Stvarna izvedba sustava digitalnog vođenja
Diskretni ekvivalent sheme sa slike 2.4.5 prikazan je na slici 2.4.6.
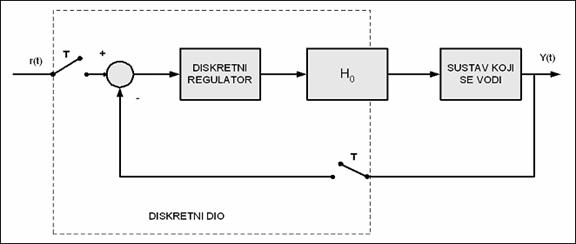
Slika 2.4.6. Stvarna izvedba sustava digitalnog vođenja
Blok dijagrami na slici 2.4.6 i 2.4.4 su ekvivalentni zbog toga što se prema blokovskoj algebri diskretnih sustava uzorkivač prebacuje ispred točke sumacije tako da se prebaci u svaku ulaznu granu sumatora pa ćemo u nastavku shemu na slici 2.4.4 uzeti kao referentnu pri izučavanju analize i sinteze diskretnih sustava vođenja.
Sustav koji sadrži samo diskretne komponente nazivamo diskretni sustav (eng. Discret-Time System), sustav koji sadrži samo analogne (kontinuirane) komponente nazivamo kontinuirani sustav (eng. Continuous-Time System), a sustav koji je sadrži i analogni (kontinuirani) dio i diskretni dio obično se naziva uzorkovani sustav (eng. Sampled-data System). U biti svi sustavi digitalnog vođenja su uzorkovani sustavi zato što je dio koji se vodi uvijek kontinuiran. Iako postoje postupci analize i sinteze takvog mješovitog, uzorkovanog sustava, obično se analiza i sinteza provode tako da se cijeli sustav prebaci ili u kontinuirani oblik ili u diskretni oblik.
Prebacivanje diskretnog sustava u kontinuirani matematički je dosta složenije i nepreglednije pa se ne koristi. Uobičajeno je da se kontinuirani dio sustava prebaci u diskretni oblik. Jedini problem analize sustava u diskretnom području je taj što je izlaz iz kontinuiranog dijela sustava u biti kontinuiran, a njegovim prebacivanjem u diskretno područje dobijemo diskretni izlaz koji je točan samo u trenucima uzorkovanja. Što se događa između dva trenutka uzorkovanja, uobičajena analiza u diskretnom području (koja se temelji na Z - transformaciji) ne otkriva. Zanima li nas ipak precizni proračun signala i između dva trenutka uzorkovanja, trebamo koristiti specijalnu analizu temeljenu na modificiranoj Z – transformaciji koja je složenija. U nastavku ćemo govoriti i o njoj, međutim za praktičnu upotrebu, ukoliko je period uzorkovanja dovoljno mali, dostatno je poznavati izlaz sustava samo u trenucima uzorkovanja i pretpostaviti linearnu interpolaciju signala između dva trenutka uzorkovanja.
