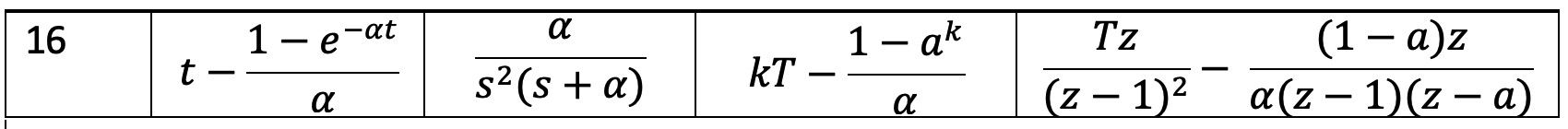3.3. Z - transformacija

Cilj: Z - transformacija je operatorski postupak pogodan za rješavanje jednadžbi diferencija, slično kao što je Laplaceova transformacija operatorski postupak za rješavanje diferencijalnih jednadžbi. U ovom poglavlju se uče temeljne postavke Z - transformacije.

Neka je x(t) kontinuirana funkcija, a x*(t) njen diskretni oblik definiran slijedom diskretnih vrijednosti x(kT) , k = 0, 1,2,...

Jednostrana Z - transformacija funkcije x*(t) definira se izrazom:

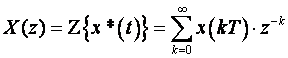(3.3.1)

gdje je z = λ + jμ kompleksna varijabla. x(kT) pri tome mora zadovoljavati određene uvjete koje većina realnih funkcija zadovoljava. Usporedimo li izraz (3.3.1) s izrazom za Laplaceovu transformaciju kontinuirane funkcije x(t):

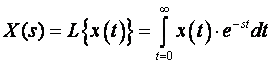(3.3.2)

gdje je s = σ + jω također kompleksna varijabla, ustanovit ćemo sličnost oblika, s tim da kod Z - transformacije integral postaje suma, kontinuirana funkcija x(t) zamjenjuje se diskretnim vrijednostima x(kT), a jezgra transformacije umjesto e^-st postaje z^-k.

Do izraza (3.3.1) možemo doći i na drugi način. Pokazali smo da se diskretna funkcija x*(t) može prikazati beskonačnim redom:

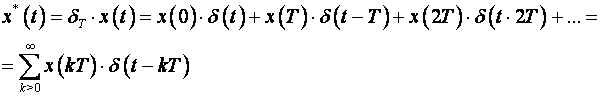(3.3.3)

Napravimo li Laplaceovu transformaciju reda (3.3.3) dobit ćemo, ukoliko primijenimo teorem pomaka Laplaceove transformacije, izraz:

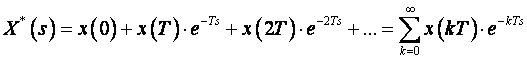(3.3.4)

S obzirom da su x(0), x(T), x(2T) ... konstante, a Laplaceova transformacija Diracove funkcije L{δ(t)}=1, uz zamjenu e^Ts=z dobijemo jednadžbu (3.3.2).

Iz identiteta z = e^Ts slijedi s = (1/T)^.ln(z) pa možemo pisati:

(3.3.5)

Osim toga kako je z = λ + jμ, a s = σ + jω pišemo:

(3.3.6)

pa vrijedi:

(3.3.7)

Važno je i zapamtiti da:

(3.3.8)

P r i m j e r :

Odredi Z - transformaciju jediničnog skoka:

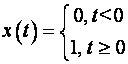
_{Najprije prelazimo u diskretni
oblik x(kT) koji je za skokovitu funkciju jednak
1 za sve k = 0,1,2, ... Prema jednadžbi (3.3.1)
slijedi:

Dobiveni red je oblika:

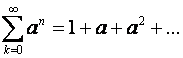
koji se jednostavno rješava.
Označimo ovaj red sa x:

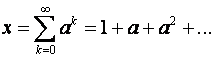
te pomnožimo lijevu i
desnu stranu s a:

Ovako dobiveni oblik oduzmimo od x:

ako su svi a^k konačni,
a to je ispunjeno ukoliko je
ostaje:
pa je rješenje reda

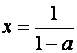
U našem primjeru a =
z^-1 pa imamo:}

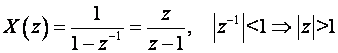
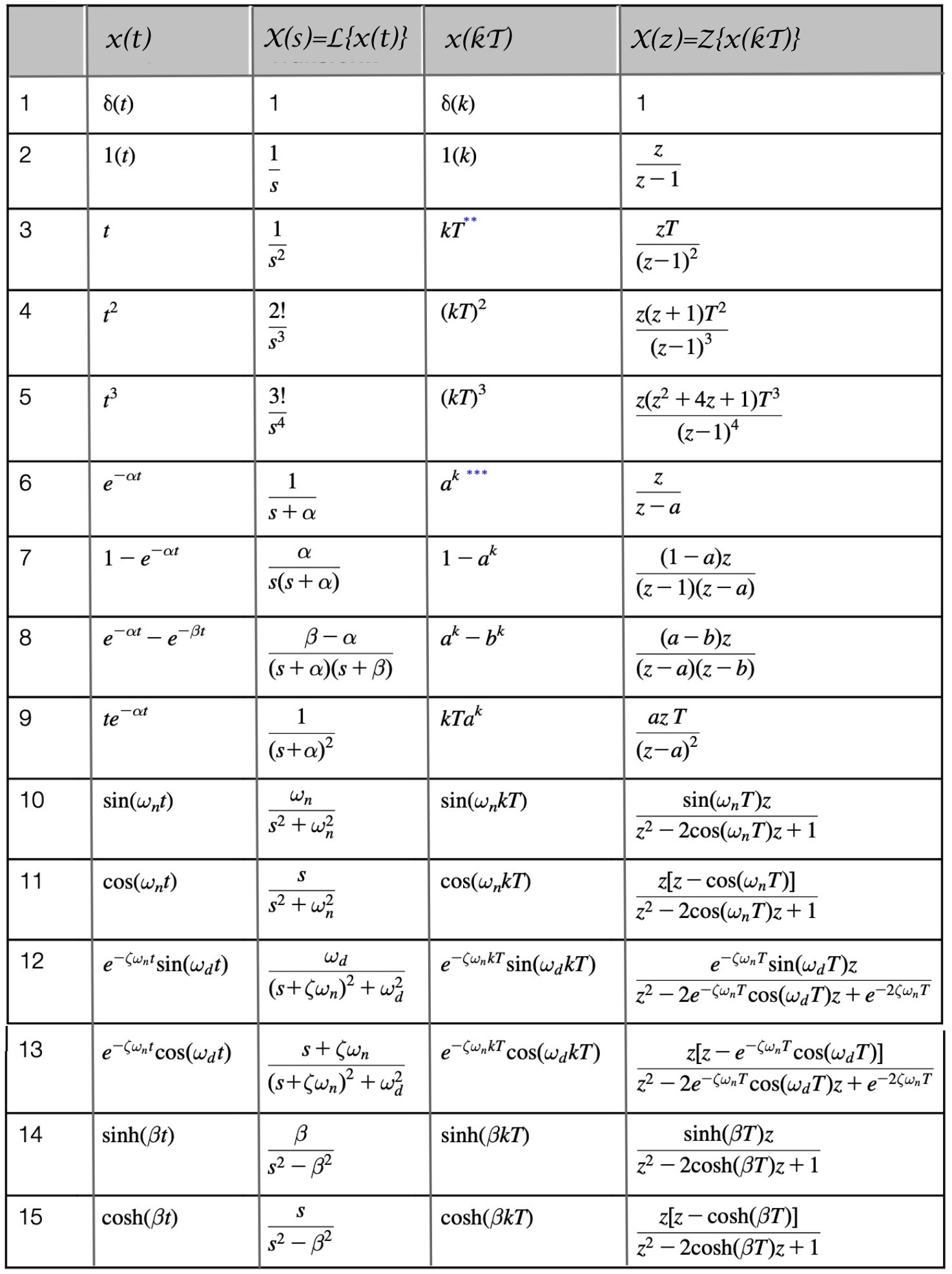
Inženjerski se Z - transformacija naravno ovako sporo ne računa, već se koriste gotove tablice Z – transformacije. Tablice se obično sastoje od tri stupca, te sadrže x(t), X(s) i X(z). Skraćena tablica za neke tipične funkcije dana je na slici 3.3.1.

Slika 3.3.1. Tipične funkcije i njihove transformacije - VAŽNO a = e^-αT

P r i m j e r :

Za funkciju definiranu Laplaceovom transformacijom:

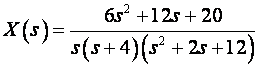
odredi Z - transformaciju.

Prvi je korak razbijanje funkcije X(s) na parcijalne razlomke:

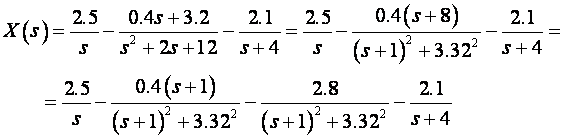
Korištenjem tablica dobijemo:

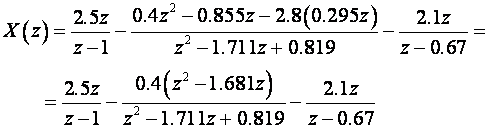
Ukoliko nam treba X(z) možemo ponovo skupiti u jedan razlomak.

Z - transformacija ima neka specifična svojstva koja izučavamo u sljedećem poglavlju.

3.3. Z - transformacija

Slika 3.3.1. Tipične funkcije i njihove transformacije - VAŽNO a = e-αT

Slika 3.3.1. Tipične funkcije i njihove transformacije - VAŽNO a = e^-αT