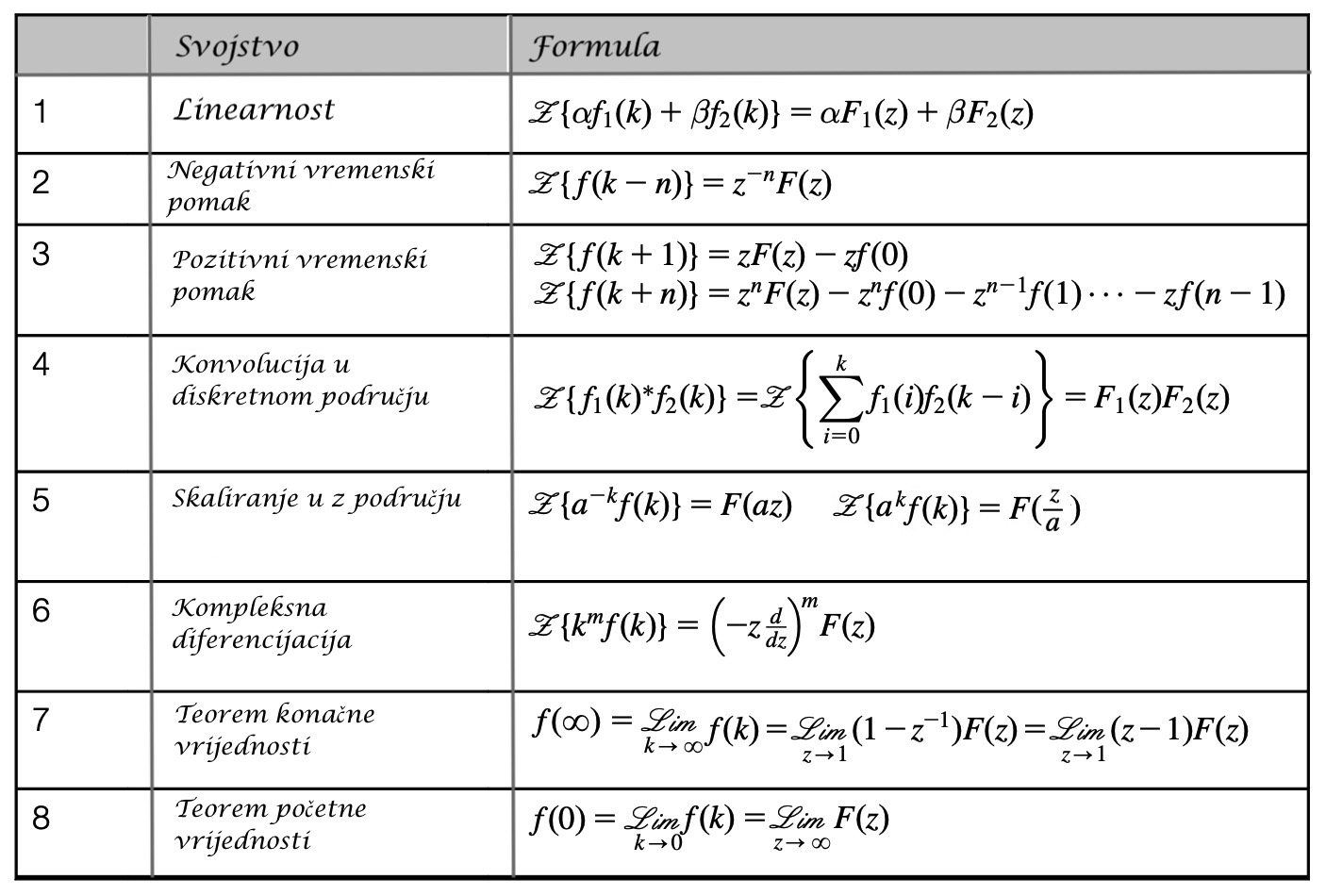
3.3.1. Svojstva Z - transformacija
1. Linearnost
(3.3.9)
gdje su α i β konstante.
2. Množenje s ak (skaliranje u z području)
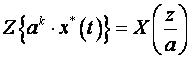(3.3.10)
3. Vremenski pomak
Općenito vrijedi:
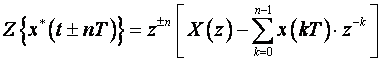(3.3.11)
Za negativne vremenske pomake x*(t-nT), suma bi išla od 0 do nekog negativnog broja, a kako je x(kT) = 0 za k<0 izraz (3.3.11) prelazi u oblik:
(3.3.12)
Za pozitivne pomake x*(t+nT),
suma se ne može zanemariti zato što ide od 0 do
pozitivnog broja, a općenito x(kT)
0 za k>0, pa ostaje:
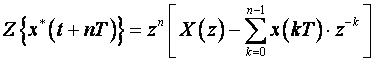(3.3.13)
Izraz (3.3.13) na neki način podsjeća na Laplaceovu transformaciju derivacije.
Pogledajmo primjer za k=1. Z - transformacija pomaknutog diskretnog signala glasi:
a Laplaceova transformacija prve derivacije je:
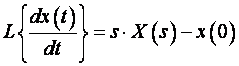
Postoji određena sličnost ali nije
potpuna.
Z{e-as X(s)} = z-i X(z) gdje je i cjelobrojni kvocjent prigušenja a i perioda uzorkovanja T: i = a/T
4. Kompleksna promjena skale
(3.3.14)
5. Teorem početne vrijednosti
(3.3.15)
6. Teorem konačne vrijednosti
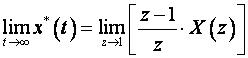(3.3.16)
Teorem ima smisla ako je sustav stabilan o čemu ćemo posebno govoriti.
Zanimljivo je usporediti teoreme konačne vrijednosti Laplaceove transformacije i Z - transformacije. Za Z - transformaciju vrijedi izraz (3.3.16), a za Laplaceovu transformaciju:
(3.3.17)
Veza između kompleksne varijable z i s je z = eTs, iz čega direktno slijedi da z → 1 ukoliko s → 0. Osim toga Z - transformacija jediničnog skoka je z/(z-1) (vidi tablicu), a njegova Laplaceova transformacija 1/s pa ima smisla što se u jednadžbi (3.3.16) pojavljuje (z-1)/z na mjestu gdje u jednadžbi (3.3.17) dolazi s.
