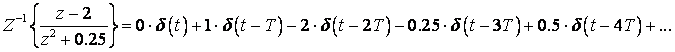3.3.2. Inverzna Z - transformacija
Sjetimo se da smo Z - transformaciju uveli kako bismo lakše rješavali jednadžbe diferencija s obzirom da se one u z području prebacuju u algebarske jednadžbe. Kako nas zanima što se s našim diskretnim sustavom događa u vremenskoj domeni dobiveno rješenje X(z) treba se vratiti natrag u diskretni oblik x*(t). Iz poznate Z - transformacije trebamo rekonstruirati slijed x(kT), k = 0,1,2,...
Inverznu Z - transformaciju možemo provesti na dva načina – analitički i numerički, a svaki od ovih postupaka ima i svoje dvije pod metode:
1. Analitički postupak
a) integral inverzije
b) razvoj u parcijalne razlomke
2. Numerički postupak
a) direktno dijeljenje
b) digitalno filtriranje
Analitički postupak - integral inverzije
Integral inverzne Z – transformacije definiran je izrazom:
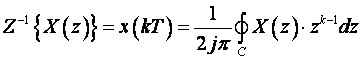 (3.3.18)
(3.3.18)
gdje je C kontura integracije u z ravnini koja okružuje singularne točke (nule i polove) funkcije X(z) . zk-1.
U inženjerskim primjenama ovaj se postupak ne koristi, pa ga dublje nećemo ni razmatrati. Integriranje u kompleksnoj ravnini je previše složeno a do rezultata možemo doći puno jednostavnije.
Analitički postupak - razvoj u parcijalne razlomke
Postupak je isti kao kod inverzne Laplaceove transformacije. Funkcija u z području se najprije razbije na parcijalne razlomke, a onda se svaki parcijalni razlomak jednostavno vraća u vremensko područje korištenjem tablica Z – transformacije. Razlika je jedino u tome što se u red parcijalnih razlomaka razvija X(z)/z. Tek nakon razvoja, desna se strana množi sa z, pa se koriste tablice.
P r i m j e r :
Dijelimo izraz sa z:
Iz tablica dobijemo
Numerički postupak - direktno
dijeljenje
X(z) se nastoji razviti u red potencija:
Iz čega se korištenjem teorema pomaka i činjenice da je
Z - transformacija Diracove funkcije
δ(t) jednaka jedinici, dobije:
Do izraza (3.3.19) dolazi se jednostavnim dijeljenjem brojnika
i nazivnika funkcije X(z).
P r i m j e r :
Dijelimo:
itd.
Dakle imamo x(0) = 1, x(T)=0.5, x(2T)=0.25, ... pa je:
Ponekad je dobro prije dijeljenja brojnik i nazivnik
podijeliti s najvećom potencijom od z:
ao treba uvijek biti jednak jedinici. Ukoliko nije
sve koeficijente trebamo najprije podijeliti s ao.
Kako je za realne sustave m ≤ n dijelimo brojnik i nazivnik sa zn pa dobijemo:
P r i m j e r :
Uzmimo isti primjer kao prije:
Dijelimo:
itd.
pa je isto kao i prije
Postupak se temelji na promatranju funkcije u z području kao
prijenosne funkcije digitalnog filtra kod kojega računamo odziv na Diracovu
δ pobudu. Najbolje ga je ilustrirati primjerom:
P r i m j e r :
najprije podijelimo brojnik i nazivnik sa z2:
Križno množenje daje:
Prebacimo izraz u vremensko područje koristeći teorem
pomaka:
odnosno:
vrijedi
Jednadžbu rješavamo iterativno:
itd.
Rješenje je kao i kod direktnog dijeljenja beskonačni red:
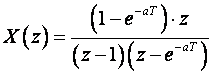
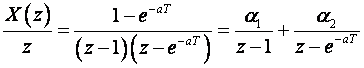
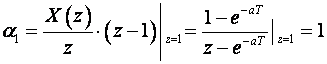
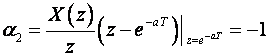
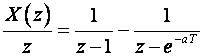
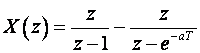
![]() pa je:
pa je:![]()
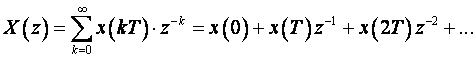 (3.3.19)
(3.3.19)![]() (3.3.20)
(3.3.20)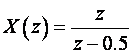
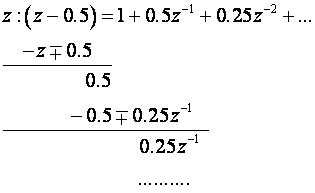
![]()
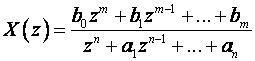 (3.3.21)
(3.3.21)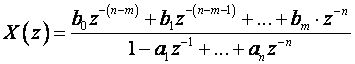 (3.3.22)
(3.3.22)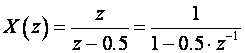
![]()
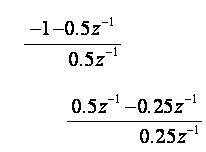
![]()
Numerički postupak - digitalno
filtriranje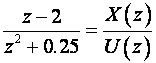
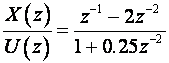
![]()
![]()
![]()
![]() , dok je za ostale
, dok je za ostale
![]() . Također svi
. Također svi
![]() manji od nule jednaki su nuli.
manji od nule jednaki su nuli. ![]()
![]()
![]()
![]()
![]()