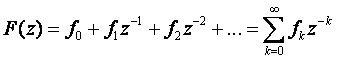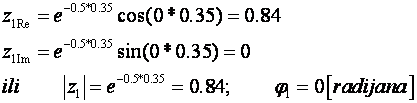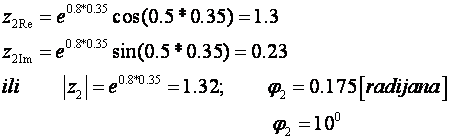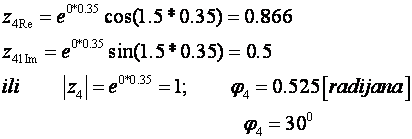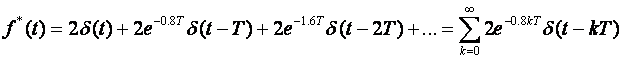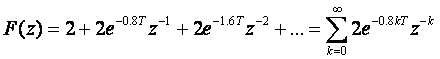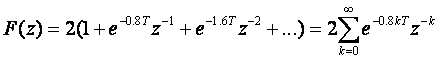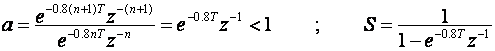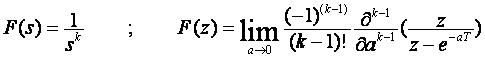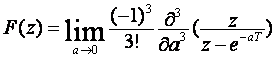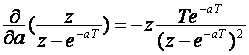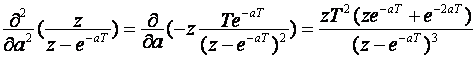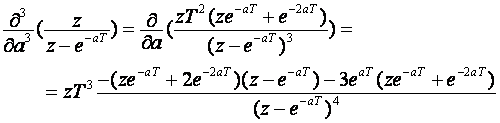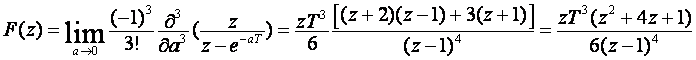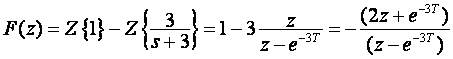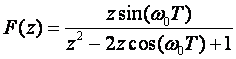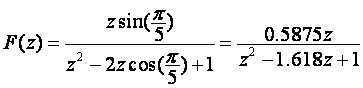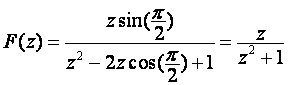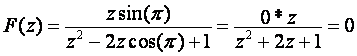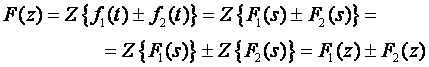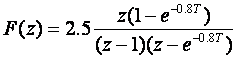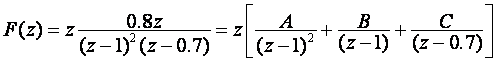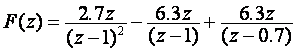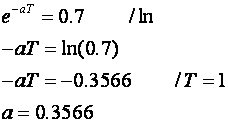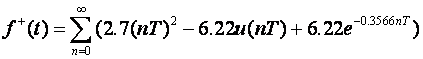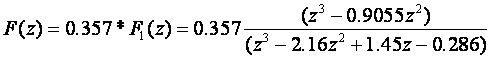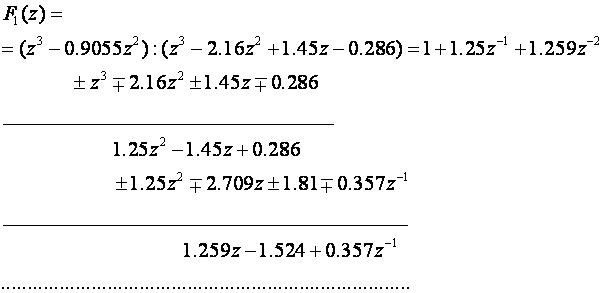3.3.3. Zadaci
1. Matematički prikaz uzorkovanih funkcija
a) vremenskom području,
b) pomoću Laplaceovog operatora,
c) pomoću z - operatora.
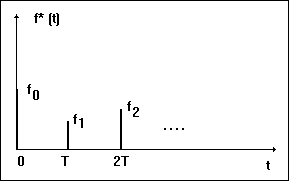
Slika 3.3.2. Uzorkovana funkcija
Svaki k-ti uzorak funkcije pojavljuje se u pripadnom diskretnom trenutku kao vrijednost fk = f(kT).
Tada je:
a) 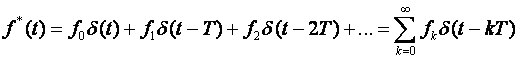
b) 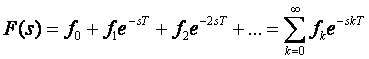
c) Budući da su s - operator i
z - operator povezani relacijom ![]() , vrijedi:
, vrijedi:
2. Preslikavanje kompleksnih točaka iz s - ravnine u z - ravninu
a) s1 = -0.5; b)
s2 = 1.1 +j 0.5 ; c) s3 = -0.5 – j ; d) s4 = j 1.5
Kompleksna z – ravnina
prikazan je na slici 3.3.3. Veza između s - operatora i z - operatora određena
je matematički kao: ![]() . Budući da je s- operator kompleksan tj.
. Budući da je s- operator kompleksan tj. ![]() , vrijedi:
, vrijedi:
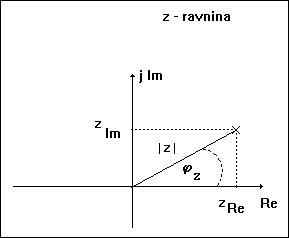
Slika 3.3.3. Kompleksna z – ravnima i z – operator
Preslikavanje se izvodi prema navedenim relacijama. Položaji odgovarajućih točaka u s - ravnini i z - ravnini prikazani su na slici 3.3.4.
a) s1 = -0.5 ili ![]()
b) s2 = 0.8 + j0.5 ili ![]()
c) s3 = -0.5 – j1 ili ![]()
d) s4 = j1.5 ili ![]()
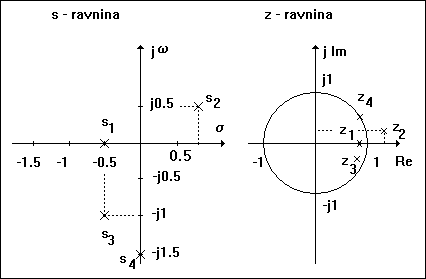
Slika 3.3.4. Zadane točke i njihovi položaji u s - ravnini i z – ravnini
3. Uzorkovane funkcije i Z - transformacija (izvedba tablice transformacija)
Na izlazu iz sklopa za uzorkovanje zadana funkcija ima matematički prepoznatljiv oblik u vremenskom području, kao:
Primjenom z - operatora funkcija je matematički opisana kao:
ili, ako izdvojimo konstantu koja je zajednička svim uzorcima i ne ovisi o položaju uzoraka, vrijedi:
označimo li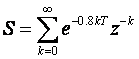 , tada vrijedi F(z) = 2 * S
, tada vrijedi F(z) = 2 * S
Izraz S se može izračunati kao:
ako je
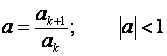
Primijenimo li relaciju na zadanu funkciju, vrijedi:
Sređivanjem dobivene sume po operatoru z, konačno možemo napisati jednostavniji matematički opis zadane, uzorkovane funkcije, ili:
Ova funkcija može se unijeti u Tablicu najčešće korištenih elementarnih funkcija za koje se Z – transformacije određuje na ovdje prikazan način. Tablica obično sadrži i dodatne informacije i sadrži sljedeće stupce:
| f(t) | F(s) | F(z) | f(kT) |
4. Primjena tablice Z-transformacije i prilagodba tabličnim oblicima
a)
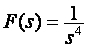
b)
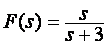
a) Prema Tablici zadana funkcija nema konačan oblik preslikavanja, već je dana u obliku izraza tj. općenit izraz u Laplaceovom području ima općenito iskazanu Z – transformaciju:
U zadanom primjeru k = 4, pa je za preslikavanje potrebno riješiti tri parcijalne derivacije po "a", ili
Prva parcijalne derivacija ima rješenje:
Druga parcijalna derivacija ima rješenje:
Treća parcijalna derivacija ima rješenje:
Konačno dobijemo rezultat preslikavanja:
b) U Tablicama ne postoji oblik za preslikavanje koji bi izravno odgovarao zadanoj funkciji. Tada se služimo dopuštenim matematičkim preinakama koje nam mogu pomoći u rješavanju.
Vrijedi:
Teoremom linearnosti (poglavlje 3.3.1) i postojećim oblicima u tablici na slici 3.3.1 možemo izvesti zadano preslikavanje.
5. Utjecaj izbora vremena uzorkovanja na Z – transformaciju
a) 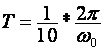
b) 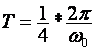
c) 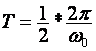
Primjenom tablice Z – transformacije vrijedi:
a) Ako je 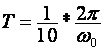 , tada se pripadna Z – transformacija funkcije
može izraziti kao
, tada se pripadna Z – transformacija funkcije
može izraziti kao
Na slici 3.3.5 prikazan je odnos izvorne kontinuirane funkcije i uzoraka dobivenih uzorkovanjem s ovako zadanim vremenom T.
b) Ako je 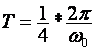 , tada se pripadna Z – transformacija funkcije
može izraziti kao
, tada se pripadna Z – transformacija funkcije
može izraziti kao
Na slici 3.3.6 prikazan je odnos izvorne kontinuirane funkcije i uzoraka dobivenih uzorkovanjem s ovako zadanim vremenom T.
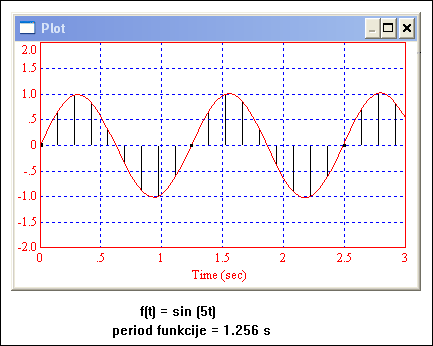
Slika 3.3.5. Odnos kontinuirane funkcije i uzoraka za T=1/(10+T0 )
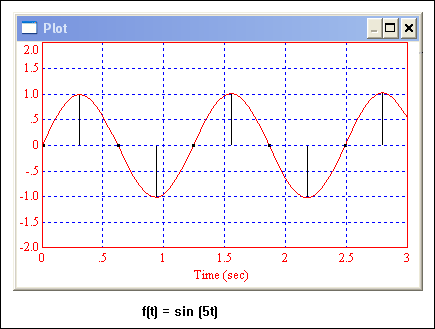
Slika 3.3.6. Odnos kontinuirane funkcije i uzoraka za T = 1/(4+T0 )
c) Ako je 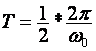 , tada se pripadna Z – transformacija funkcije
može izraziti kao
, tada se pripadna Z – transformacija funkcije
može izraziti kao
tj. uzorci kontinuirane funkcije uzimaju se samo u nul-točkama i uzorkovana slika bi prikazivala niz uzoraka vrijednosti nula.
Komentar!
Jedino u a) dijelu rješenja Z – transformacija ima prepoznatljiv oblik sinusne funkcije, a i uzorci na slici 3.3.5 relativno dobro oslikavaju izvornu funkciju. Kod b) dijela rješenja Z – transformacija dobiva teško prepoznatljiv oblik, a i slika uzoraka bi teško asocirala na sinusnu funkciju. Kod c) dijela zadatka uočljiv je apsurdan način uzorkovanja. Kvaliteta izbora vremena uzorkovanja odražava se ne samo na vremenskoj i frekvencijskoj slici funkcije, već i na izrazu Z – transformacije.
6. Utjecaj izbora vremena uzorkovanja na Z – transformaciju
Ako zadana funkcija ne predstavlja tablični oblik, do elementarnih oblika dolazi se rastavljanjem na parcijalne razlomke ili vrijedi:
Prema Teoremu linearnosti vrijedi:
Primjenom izraza na zadanu funkciju i uz tablicu sa slike 3.3.1 dobijemo:
Rezultat preslikavanja često se opet vraća na zajednički razlomak ili
7. Inverzna Z - transformacija (primjena tablica i Teorema linearnosti)
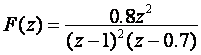 i vrijeme uzorkovana
T = 1.
i vrijeme uzorkovana
T = 1.Ako se traži inverzna Z - transformacija primjenom tablica, najprije potražimo da li se zadana funkcija nalazi u tablici. Ovdje zadana funkcija nije elementarna i stoga funkciju treba prilagoditi elementarnim oblicima rastavljanjem na parcijalne razlomke.
Uočiti! Sve elementarne funkcije Z - transformacije imaju u brojniku operator z. Primjena tablica u inverznoj Z - transformaciji imat će smisla ako se nazivnik zadane funkcije može jednostavno prikazati u kaskadnom obliku i ako se zadanoj funkciji može u brojniku izdvojiti operator z.
U ovom slučaju vrijedi:
Rješavanjem se dobije A = 2.7 ; B = - 6.3 ; C = 6.3.
Sad se funkcija može prikazati kao:
U tablici na slici 3.3.1 mogu se izdvojiti (prepoznati) sljedeći oblici:
| f(t) | F(s) | F(z) |
| u(t)-jedinična odskočna funkcija | ||
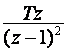 |
||
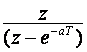 |
Sad se može iskoristiti Teorem linearnosti prema kojem je:
ili
Potrebno je, također, povezati na pravi način oblike 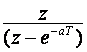 i
i ![]() ili u ovom zadatku treba povezati izraz:
ili u ovom zadatku treba povezati izraz:
Na temelju svih uvedenih relacija može se zapisati inverzna Z - transformacija, a funkcija se može prikazati u željenom obliku:
ili
ili
8. Inverzna Z - transformacija (numeričkim postupkom ili direktnim dijeljenjem)
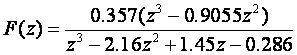
Inverzna Z – transformacija, općenito, može predstavljati preslikavanje u različita područja, Laplaceovo, vremensko – kontinuirano i vremensko – diskretno. U zadatku 6. zadana je funkcija, primjenom tablice sa slike 3.3.1, preslikana u sva tri područja. Takvo se rješenje može dobiti samo ako postoji način da se Z – transformacija zadane funkcije prikaže pomoću elementarnih, tabličnih oblika.
Nazivnik funkcije F(z) zadane u ovom zadatku prikazan je u obliku polinoma koji se ne može jednostavnim računskim operacijama svesti na produkt. U takvim slučajevima se inverznom Z – transformacijom rješenje prikazuje samo u vremensko – diskretnom području, tj. prepoznaju se samo vrijednosti uzoraka funkcije u pojedinim diskretnim trenucima.
Kad je funkcija zadana u z području u obliku razlomka najjednostavniji način da se izdvoje vrijednosti uzoraka je da se podijele polinomi brojnika i nazivnika. Za zadanu funkciju vrijedi:
Računska operacija dijeljenja može trajati po volji dugo, a rješenje inverzne Z – transformacije ili uzorci funkcije prepoznat će se u trenucima uzorkovanja vremenom T ili kao:
f(0) = 0.357 * 1
f(T) = 0.357*1.25 = 0.446
f(2T) = 0.357*1.259 = 0.449