3.4. Impulsna prijenosna funkcija
Dinamičko ponašanje sustava u kontinuiranom svijetu opisuje se diferencijalnim jednadžbama. Kako bi se olakšala analiza kontinuiranih sustava Laplaceovom se transformacijom prelazi u kompleksno s područje u kojem se diferencijalna jednadžba predstavlja algebarskom jednadžbom. Uzmimo za primjer sustav prikazan na slici 3.1 koji opisuje jednažba 3.1,
(3.2)
Uz nulte početne uvjete (na početku promatranja spremnik je prazan) algebarska jednadžba u s području glasi:
(3.4.1)
Sredimo li jednadžbu na način da na lijevoj strani ostane razlomak Y(s)/R(s) dobijemo oblik koji nazivamo prijenosna funkcija i uobičajeno ga označavamo G(s):
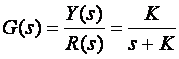(3.4.2)
Prijenosna funkcija je prema tome omjer Laplacove transformacije izlaznog i ulaznog signala sustava uz nulte početne uvjete. Možemo je promatrati i na drugi način:
Pretpostavimo da smo na ulaz sustava doveli Diracovu jediničnu impulsnu pobudu δ. Laplaceova transformacija funkcije δ je jednaka jedinici, pa iz jednadžbe (3.4.2) možemo pisati:
(3.4.3)
Y(s) je Laplaceova transformacija odziva sustava y(t) na Diracovu jediničnu impulsnu pobudu. Uobičajeno je da se odziv sustava na Diracovu jediničnu impulsnu pobudu naziva karakteristični odziv, a ponekad, pogotovo u engleskoj literaturi i impulsni odziv (eng. Impulse response), pa je u u skladu s izrazom (3.4.3) prijenosna funkcija sustava Laplaceova transformacija karakterističnog ili impulsnog odziva sustava.
Ova priča se može u potpunosti prenijeti i na diskretne sustave s tim da se umjesto Laplaceove transformacije koristi Z – transformacija, a dobivena prijenosna funkcija G(z) se naziva impulsna prijenosna funkcija sustava. Ukoliko je poznat karakteristični odziv diskretnog sustava, njegovom transformacijom u z područje automatski dobivamo impulsnu prijenosnu funkciju. Ilustrirajmo ovu ideju primjerom:
Neka je impulsni odziv diskretnog sustava dan slijedom diskretnih vrijednosti 1, 0.5, 0.25, 0, 0, ... što znači da je izlaz sustava pobuđen Diracovom pobudom:
(3.4.4)
Z - transformacija ovog impulsnog odziva je impulsna prijenosna funkcija promatranog sustava. Korištenjem teorema pomaka i tablica dobijemo:
(3.4.5)
odnosno sređivanjem:
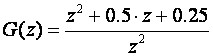(3.4.6)
Pojam impulsne prijenosne funkcije može se, slično kao i kod kontinuirane prijenosne funkcije, poopćiti na način da je definiramo kao omjer Z - transformacije izlaznog i ulaznog signala sustava uz nulte početne uvjete:
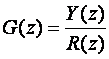(3.4.7)
Primjer:
Za
diskretni sustav
opisan jednadžbom
diferencija
y(k+1)-y(k) =
u(k+1)
izračunaj odziv na
jedinični skok uz
nulte početne
uvijete koristeći
impulsnu
prijenosnu
funkciju.
Rješenje:
Najprije se
prebacujemo iz
diskretnog
područja u z
područje:
z Y(z) – Y(z) = z
U(z)
Impulsna
prijenosna
funkcija G(z)
sustava je omjer Z
transformacije
izlaznog i ulaznog
signala uz nulte
početne uvjete:
G(z) = z/(z-1)
Kako je Z
transformacija
jediničnog skoka
U(z) = z/(z-1)
odziv sustava će
biti:
Y(z) = G(z) * U(z)
=
[z/(z-1)]*[z/(z-1)]
= [z/(z-1)]2
= z*[z/(z-1)2]
U Tablicama
Z-transformacije (Poglavlje
3.3)
tablični oblik je
Tz/(z-1)2
koji se prebacuje
u uzlaznu sekvencu
kT. Uz to na
početku imamo i
množenje sa z što
nam to teormu
pomaka daje pomak
za jedan diskretni
trenutak vremena. kako nama nedostaje u brojniku T dodajemo T/T, pa ćemo dobiti
pa će sekvenca
izlaznog signala
biti:
y(k) = (k+1)T/T = k+1 , za
k=0,1,2,3,...
Svojstva
impulsne prijenosne funkcije
Za diskretni sustav opisan jednadžbom diferencija
y(k+1)-y(k) = u(k+1)
izračunaj odziv na jedinični skok uz nulte početne uvijete koristeći impulsnu prijenosnu funkciju.
Rješenje:
Najprije se prebacujemo iz diskretnog područja u z područje:
z Y(z) – Y(z) = z U(z)
Impulsna prijenosna funkcija G(z) sustava je omjer Z transformacije izlaznog i ulaznog signala uz nulte početne uvjete:
G(z) = z/(z-1)
Kako je Z transformacija jediničnog skoka U(z) = z/(z-1) odziv sustava će biti:
Y(z) = G(z) * U(z) = [z/(z-1)]*[z/(z-1)] = [z/(z-1)]2 = z*[z/(z-1)2]
U Tablicama Z-transformacije (Poglavlje 3.3) tablični oblik je Tz/(z-1)2 koji se prebacuje u uzlaznu sekvencu kT. Uz to na početku imamo i množenje sa z što nam to teormu pomaka daje pomak za jedan diskretni trenutak vremena. kako nama nedostaje u brojniku T dodajemo T/T, pa ćemo dobiti pa će sekvenca izlaznog signala biti:
y(k) = (k+1)T/T = k+1 , za k=0,1,2,3,...
Impulsna prijenosna funkcija ima nekoliko važnih svojstava:
a) Periodičnost – Prebacimo li G(z) u s područje zamjenom z = eTs dobit ćemo funkciju G*(s) koja je periodična funkcija s imaginarnom periodom jωS = j2 π/T. Drugim riječima polarni dijagram funkcije G*(s) za promjenu frekvencije ω od 0 do ωS je isti kao i polarni dijagram za promjenu frekvencije ω od kωS do (k+1)ωS (k je veći od 0).
b) Realnost – konačnost – Impulsna prijenosna funkcija G(z) uvijek je realna za z=1 i z=-1 i konačna za z=1 ukoliko je G(s) sustav 0-te vrste (nema pol u ishodištu).
c) Povezanost polova – Polovi zk impulsne prijenosne funkcije G(z) u z ravnini i polovi sk prijenosne funkcije G(s) u s ravnini povezani su izrazom zk=eTsk. Iz toga slijedi da je red (ukupan broj polova) impulsne prijenosne funkcije jednak redu prijenosne funkcije G(s).
d) Dodavanje (ispuštanje) nula – Nule impulsne prijenosne funkcije G(z) i prijenosne funkcije G(s) nisu povezane ni na koji način, osim što dodavanje (ispuštanje) nula prijenosne funkcije G(s) uzrokuje promjenu konstante pojačanja impulsne prijenosne funkcije G(z). Dodavanje (ispuštanje) nula isto tako ni na koji način ne utječe na polove impulsne prijenosne funkcije. Objašnjenje se krije u načinu prijelaza iz G(s) u G(z). Jedan od postupaka temelji se na razvoju G(s) u parcijalne razlomke. Parcijalnih razlomaka ima onoliko koliko ima polova, a nule djeluju samo na konstante pojačanja pojedinog parcijalnog razlomka.
Impulsna prijenosna funkcija sustava koji se vodi od izuzetne je važnosti za projektiranje digitalnog sustava vođenja, pa se postavlja praktično pitanje:
Kako odrediti impulsnu prijenosnu funkciju sustava kojeg namjeravamo voditi?
Moguća su dva pristupa: teorijski i eksperimentalni. Kod teorijskog sustav se najprije modelira u kontinuiranom području i izvede se njegova kontinuirana prijenosna funkcija G(s). Nakon toga se nekom od metoda prelazi u diskretno područje i proračunava impulsna prijenosna funkcija G(z). Kod eksperimentalnog koristi se neki od postupaka identifikacije impulsne prijenosne funkcije.
Međutim
prije nego se objasne obje metode nužno je
uvesti pojam ekvivalentnog sustava
i ekvivalentne impulsne prijenosne
funkcije koji obrađujemo u
sljedećem poglavlju.