3.2. Rješavanje jednadžbi diferencija
Diskretni regulacijski sustav sa slike 3.3 opisali smo linearnom jednadžbom diferencija prvog reda:
![]()
Sada nam je zadatak riješiti jednadžbu na temelju poznavanja početnog uvjeta y(0) i diskretnog slijeda referentnog signala r(kT), k = 0, 1, 2...
Tri su temeljna pristupa rješavanju jednadžbi diferencija:
a) rekurzivne formule,
b) analitičke metode,
c) operatorski postupak (Z - transformacija).
Rekurzivne formule jednostavan su i direktan
pristup u kojem se slijedno računaju y(T), y(2T), y(3T), itd. Jednadžbu
(3.2.1) najprije vratimo u izvorni oblik (3.6) koji uz malo sređivanja daje:
![]()
Rekurzivni postupak daje slijed izlaznog signala sustava u trenucima T, 2T, 3T itd.:
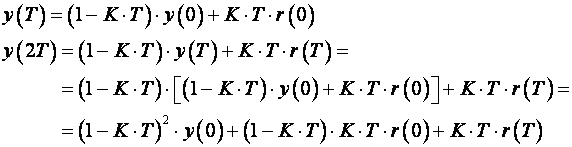
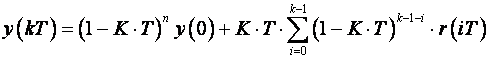 (3.2.3)
(3.2.3)
Jednadžba (3.2.3) je opće rješenje jednadžbe diferencija (3.2.1), kao što je jednadžba (3.2) opće rješenje diferencijalne jednadžbe (3.1). Opće rješenje možemo dobiti i analitičkim metodama, koje se u praksi obično ne koriste pa ih ovdje nećemo ni razmatrati.
Treći je postupak operatorski postupak kod kojeg se izborom prikladne
transformacije jednadžba diferencija nastoji prebaciti u lakše rješivi
oblik, a to je algebarska jednadžba. Sličan se postupak koristi kod
rješavanja diferencijalnih jednadžbi. Primjenom linearne integralne
transformacije poznate po imenu Laplaceova transformacija
diferencijalna se jednadžba iz vremenskog t područja prebaci u kompleksno s
područje u kojem se ona transformira u algebarsku jednadžbu. Algebarska je
jednadžba lako rješiva (rješavanje algebarskih jednadžbi uči se još u
osnovnoj školi, dok se diferencijalne jednadžbe spominju tek na fakultetu).
Kad se u s području dođe do rješenja pribjegne se inverznoj Laplaceovoj
transformaciji kojom se iz s područja vraćamo natrag u t područje koje nas u
biti i zanima. Nama je zanimljivo doznati što se događa u vremenskoj domeni
u kojoj mi i živimo.
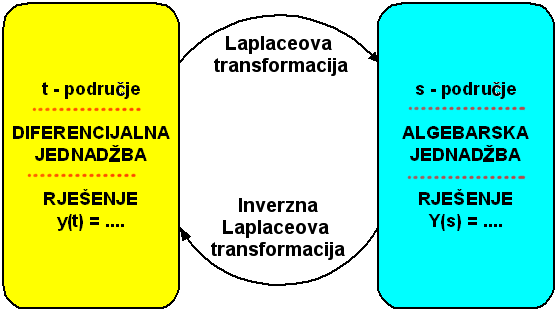
Slika 3.2.1. Rješavanje diferencijalnih jednadžbi korištenjem Laplaceove transformacije
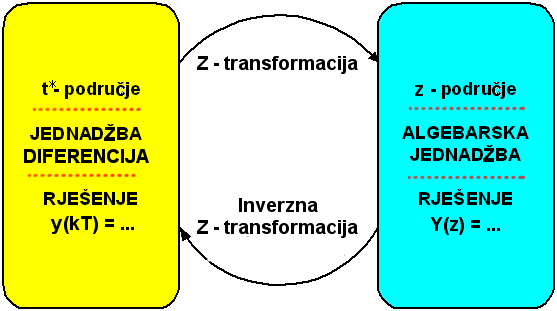
Kod rješavanja jednadžbi diferencija postupak je identičan samo što se umjesto Laplaceove transformacije koristi Z - transformacija koja jednadžbe diferencija iz diskretnog kT područja prebaci u algebarske jednadžbe kompleksnog Z - područja. Algebarska se jednadžba riješi, a rješenje se inverznom Z - transformacijom vrati natrag u kT područje.
Slika 3.2.2. Rješavanje jednadžbi diferencija korištenjem Z - transformacije
Vezu između signala u kontinuiranom vremenskom, diskretnom vremenskom, Laplceovom i Z području možemo predočiti i sljedećom slikom:
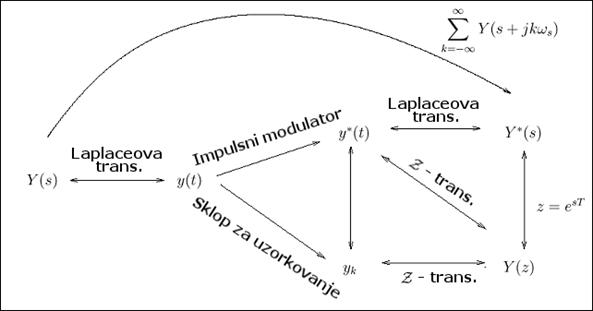
Slika 3.2.3. Veza između signala u vremenskom, Laplaceovom i Z području
Kontinuirani vremenski signal y(t) s jedne se strane prebacuje u Laplaceov signal Y(s) Laplaceovom transformacijom. S druge strane možemo ga prebaciti i u diskretno područje impulsnim modulatorom, pa dobiti modulirani slijed impulsa y*(t):
![]()
ili sklopom za uzorkovanje koji na svom izlazu daje diskretne vrijednosti y(kT) (koje često pišemo i yk ). Diskretni signal y*(t) možemo dalje Laplaceovom transformacijom prebaciti u Lapleceovo područje i dobiti Y*(s). Razlika između Y*(s) i Y(s) je u tome što je kod Y*(s) osnovi spektar signala Y(s) proširen po cijelom frekvencijskom području i ponavlja se oko kružne frekvencije uzimanja uzoraka ωS:
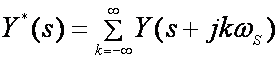 (3.2.5)
(3.2.5)
Do signala u Z – području Y(z) možemo doći na dva načina:
a) varijablu z definiramo kao z = esT , pa iz Y*(s) zamjenom svakog s-a sa pređemo u Y(z), ili
b) na diskretni signal y(kT) primijenimo Z – transformaciju
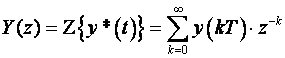
o čemu detaljno govorimo u sljedećem poglavlju 3.3.
Rekurzivni se postupak rješavanja jednadžbi diferencija koristi za numeričko rješavanje diferencijalnih jednadžbi. Problem je jedino u tome što se diferencijalna jednadžba može na više načina prebaciti u jednadžbu diferencija, pa se dobivena rješenja mogu međusobno razlikovati. Postupak prebacivanja diferencijalne jednadžbe u jednadžbu diferencija nije važan samo zbog rješavanja diferencijalne jednadžbe. Na njemu će se kasnije temeljiti svi postupci aproksimacije kontinuiranih sustava diskretnim, pa ga zato detaljno razmatramo.