3.2.1. Aproksimacija diferencijalne jednadžbe jednadžbom diferencija
Kod prebacivanja diferencijalne jednadžbe u jednadžbu diferencija dva su temeljna pristupa:
a) zamjena derivacija diferencijama (unaprijednom, povratnom ili centralnom), i
b) pretvaranje diferencijalne jednadžbe u integralnu jednadžbu uz numeričko rješavanje integrala nekim od pravila numeričke integracije na primjer unaprijedno pravokutnim, povratno pravokutnim ili trapeznim pravilom.
Prvi od njih smo već susreli pa ćemo ga samo ilustrirati primjerom:
P r i m j e r :
Prebaci
![]()
u jednadžbu diferencija i riješi je u diskretnom području. Na ulazu je jedinični skok, a početni uvjet je jednak nuli.
Primjenjujemo sva tri postupka zamjene derivacija diferencijama:
a)
Povratna diferencija
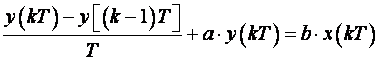
Nakon sređivanja dobijemo:
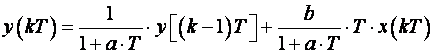
b)
Unaprijedna diferencija
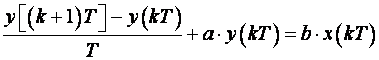
Nakon sređivanja dobijemo:
![]()
Snižavanjem reda ove jednadžbe za 1 (zamjenom k+1=k i k=k-1 dobijemo:
![]()
c)
Centralna diferencija
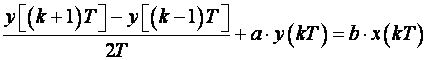
![]()
Snižavanjem reda (zamjena k+1=k, k=k-1, k-1=k-2) slijedi:
![]()
Neka su a=1, b=0.5, T =0.1.
Do sada imamo tri različite jednadžbe diferencija dobivene iz iste diferencijalne jednadžbe:
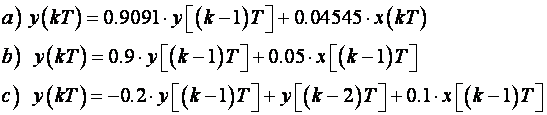
Sljedeći je korak uvrstiti y(0) = 0 i x(0) = x(T) = x(2T) = … = 1.
Rezultat su sljedeći nizovi (diferencijalna_diskretna.vsm):
a) Povratna b) Unaprijedna c) Centralna d)Točno
0 0 0 0
0.05 0 0 0.04758
0.09545 0.05 0.1 0.09063
0.1368 0.095 0.08 0.1296
0.1743 0.1355 0.184 0.1648
0.2085 0.172 0.1432 0.1967
0.2395 0.2048 0.2554 0.2256
0.2677 0.2343 0.1921 0.2517
0.2933 0.2609 0.3169 0.2753
0.3166 0.2848 0.2287 0.2967
0.3378 0.3063 0.3712 0.3161
0.3571 0.3257 0.2545 0.3336
0.3746 0.3431 0.4203 0.3494
0.3905 0.3588 0.2704 0.3637
0.405 0.3729 0.4662 0.3767
0.4181 0.3856 0.2772 0.3884
0.4301 0.3971 0.5108 0.3991
0.4409 0.4073 0.2751 0.4087
0.4508 0.4166 0.5557 0.4174
0.4598 0.425 0.2639 0.4252
0.4679 0.4325 0.6030 0.4323
Rezultati dobiveni primjenom povratne i unaprijedne diferencije su slični s tim da unaprijedna diferencija kasni za jedan diskretni trenutak vremena. Međutim kod primjene centralne diferencije u signalu postoji superponirana nestabilna oscilatorna komponenta. Razlog je taj što je period uzimanja uzoraka previše velik pa se jedan od polova prijenosne funkcije diskretnog sustava nalazi u nestabilnom području (Napomena: o prijenosnoj funkciji diskretnog sustava koju zovemo impulsna prijenosna funkcija detaljno govorimo u poglavlju 3.4, a o problemu stabilnosti u poglavlju 4.1) .
Smanjimo li period uzimanja uzoraka razlike postaju manje, ali centralna diferencija i dalje daje nestabilan odziv pa se ona obično ne koristi.
Korištenje postupka prebacivanja diferencijalne jednadžbe u integralnu jednadžbu
Pogledajmo sada postupak prebacivanja diferencijalne jednadžbe u integralnu jednadžbu na primjeru jednadžbe prvog reda iz prethodnog primjera. Integrirajmo lijevi i desni dio diferencijalne jednadžbe
![]()
Rezultat je
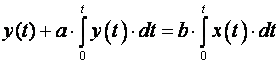
Označimo integrale izrazima
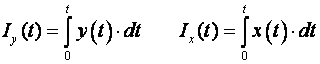 (3.2.7)
(3.2.7)
Kako integral predstavlja površinu ispod krivulje varijable y(t), odnosno x(t), u trenutku t=kT integral je jednak vrijednosti integrala u prethodnom diskretnom trenutku (k-1)T plus površina ispod krivulje između trenutaka (k-1)T i kT (slika 3.2.4 a). Za integral Iy vrijedi:
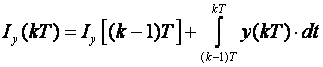 (3.2.8)
(3.2.8)
Dio integrala između diskretnih trenutaka (k-1)T i kT može se i aproksimirati površinom pravokutnika čiju jednu stranicu čini period uzorkovanja T, a drugu stranicu:
a) vrijednost amplitude na početku intervala y[(k-1)T],
b) vrijednost amplitude na kraju intervala y(kT), ili
c) vrijednost srednje vrijednosti amplitude između ta dva intervala {y(kT) + y[(k-1)T]}/2.
U prvom slučaju govorimo o aproksimaciji integrala unaprijednim pravokutnim pravilom (slika 3.2.4b)
![]() (3.2.9)
(3.2.9)
u drugom slučaju govorimo o aproksimaciji integrala povratnim pravokutnim pravilom (slika 3.2.4c)
![]() (3.2.10)
(3.2.10)
a u trećem slučaju trapeznim pravilom (slika 3.2.4d)
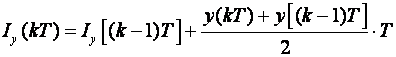 (3.2.11)
(3.2.11)
Kod unaprijednog pravokutnog pravila dobivena vrijednost integrala je manja od stvarne vrijednosti, kod povratnog pravokutnog pravila veća od stvarne vrijednosti, dok je kod trapeznog pravila najbliža stvarnoj vrijednosti integrala.
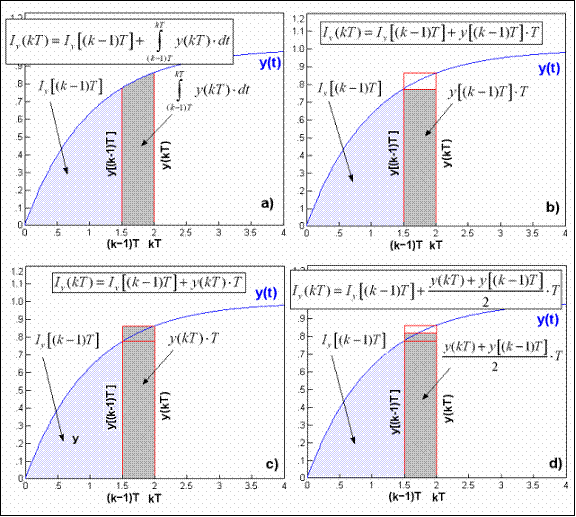
Slika 3.2.4. Računanje integrala u trenutku t = kT
Primjer:
Vratimo se na primjer diferencijalne jednadžbe
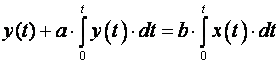
Zanima nas rješenje u trenutku t=kT. Na ulazu je jedinični skok pa je integral Iy za t=kT upravo i jednak vrijednosti kT. Dalje pišemo
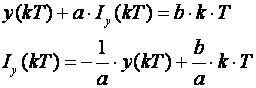
Snizimo vrijeme za jedan diskretni trenutak:
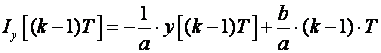
Sada aproksimiramo integral nekom od transformacijskih formula:
a) Pravokutno povratno pravilo
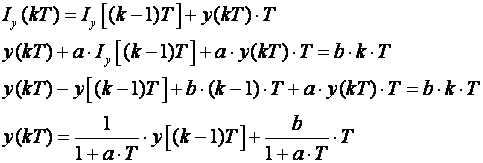
a to je isti rezultat koji smo dobili za povratnu diferenciju s tom razlikom da nema pomaka ulaznog signala.
b) Pravokutno unaprijedno pravilo
![]()
Uvrstimo u jednadžbu
![]()
i zamijenimo Iy [(k-1)T] s izrazom koji smo prije izveli:
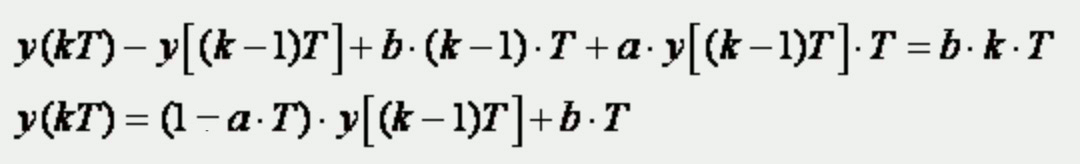
a to je isti rezultat koji smo dobili za unaprijednu diferenciju s tom razlikom da nema pomaka ulaznog signala.
c) Trapezno pravilo
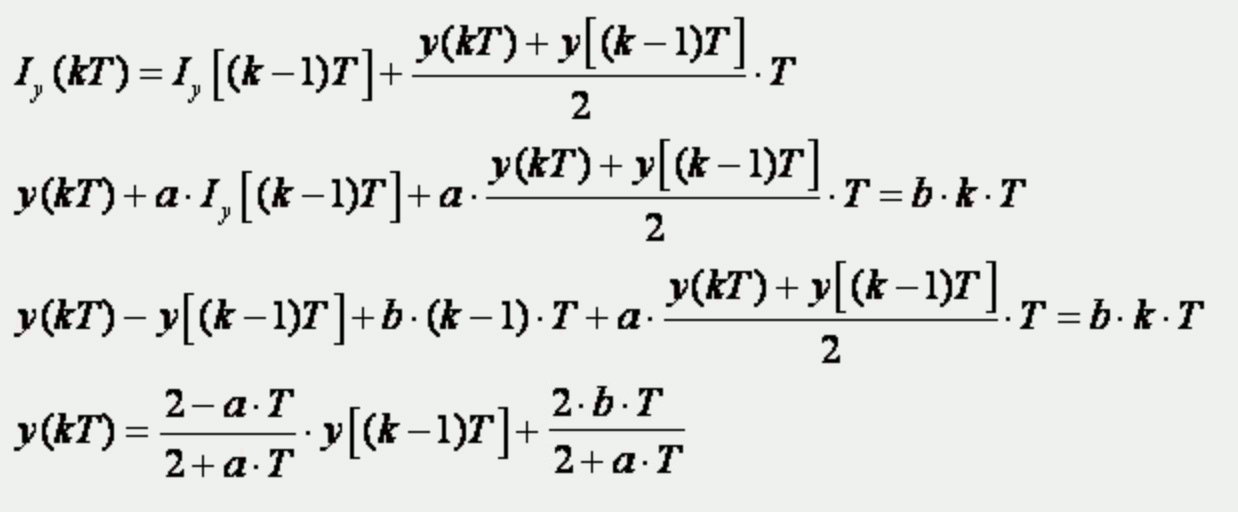
što je novi rezultat.
Uvrstimo li a=1, b=0.5, T =0.1 za sva tri pravila dobijemo:
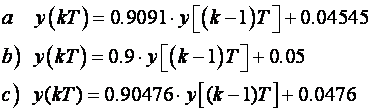
Po vrijednostima koeficijenata rezultat trapeznog pravila je između vrijednosti dobivenih za pravokutna pravila. Za usporedbu su dane i točne vrijednosti rješenja diferencijalne jednadžbe u istim vremenskim trenucima. Vrijednosti dobivene trapeznim pravilom se skoro potpuno poklapaju (diferencijalna_diskretna2.vsm):
k a) Pov. prav.pr. b) Prav. unap. c) Trap. pr. d)Točno
0 0 0 0 0
1 0.04545 0.05 0.0476 0.04758
2 0.08677 0.095 0.09067 0.09063
3 0.1243 0.1355 0.1296 0.1296
4 0.1585 0.172 0.1649 0.1648
5 0.1895 0.2048 0.1968 0.1967
6 0.2177 0.2343 0.2256 0.2256
7 0.2434 0.2609 0.2518 0.2517
8 0.2667 0.2848 0.2754 0.2753
9 0.2879 0.3063 0.2967 0.2967
10 0.3072 0.3257 0.3161 0.3161
11 0.3247 0.3431 0.3336 0.3336
12 0.3407 0.3588 0.3494 0.3494
13 0.3551 0.3729 0.3637 0.3637
14 0.3683 0.3856 0.3767 0.3767
15 0.3803 0.3971 0.3884 0.3884
16 0.3912 0.4073 0.399 0.3991
17 0.4011 0.4166 0.4086 0.4087
18 0.4101 0.425 0.4173 0.4174
19 0.4182 0.4325 0.4252 0.4252
20 0.4257 0.4392 0.4323 0.4323
Naravno da ovo nisu jedini načini aproksimacije integrala. Još točniju aproksimaciju daje Simpsonovo pravilo, pravilo Runge Kutta n-tog reda, Newton-Cotesova formula itd. Ove se metode prvenstveno koriste za potrebe numeričke integracije i simulacije kontinuiranog sustava na digitalnom računalu. Na primjer VisSim nudi 7 različitih postupaka numeričke integracije (Simulate > Simulation Properties). Što je metoda točnija to će odziv simuliranog sustava biti bliže odzivu polaznog sustava. Međutim problematika numeričke simulacije prelazi okvire ovog rada. Nama aproksimacija integrala najčešće treba za prebacivanje kontinuiranog opisa sustava u diskretni opis (zamjena prijenosne funkcije tzv. impulsnom prijenosnom funkcijom), a tu se obično zaustavljamo na trapeznom pravilu koje daje u većini slučajeva zadovoljavajuće rezultate – vidi poglavlje 3.4.
Zaključimo: Kod prebacivanja kontinuiranih sustava u diskretni oblik obično se koristi zamjena derivacije povratnom ili unaprijednom diferencijom ili zamjena integrala trapeznim pravilom. Trapezno pravilo daje najtočniji rezultat, pa se na njemu temelje i neki od aproksimacijskih postupaka diskretizacije kontinuirane prijenosne funkcije (vidi poglavlje 3.4.2.2)