3.4.2.2. Aproksimacijski postupci
Aproksimacijski postupci se temelje na jednadžbama koje na neki način povezuju varijablu s i varijablu z. Postupak je takav da se na određeni način proračuna zamjenska formula s=f(z) te se napravi zamjena:
(3.4.22)
Tustinova aproksimacija
Pogledajmo postupak na primjeru Tustinove aproksimacije (A.Tustin, A method of analysing the behavior of linear system in terms of time series, Journal of IEE, London, Vol. 94, pt. IIA, pp. 130 - 142, 1947)
(Napomena: Tustinova aproksimacija spada u širu skupinu tkz. bilinearnih transformacija o kojima više govorimo u poglavlju 4.4.1)
Krećemo iz vremenskog područja od jednadžbe integrala
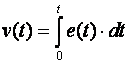(3.4.23)
Pređimo u diskretno područje. Vrijednost integrala u diskretnom trenutku kT (vidi sliku 3.4.8) predstavlja ukupnu površinu ispod krivulje e(t) od 0 do trenutka kT. Možemo je približno izračunati iz vrijednosti integrala u prethodnom trenutku (k-1)T (površina ispod krivulje e(t) od 0 do (k-1)T) i približnog proračuna površine ispod integrala između trenutaka (k-1)T i kT.
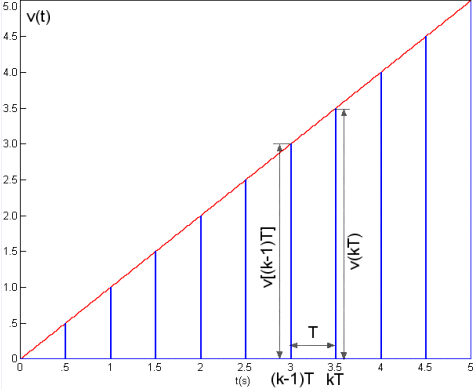
Slika 3.4.8. Diskretizacija integrala
Tri su moguća načina aproksimativnog proračuna ove manje površine:
a) unaprijednim pravilom, tako da se površina ispod krivulje između vremenskih trenutaka (k-1)T i kT računa produktom e[(k-1)T].T,
b) povratnim pravilom, tako da se površina ispod krivulje između vremenskih trenutaka (k-1)T i kT računa produktom e(kT).T, i
c) trapeznim pravilom, tako da se površina ispod krivulje između vremenskih trenutaka (k-1)T i kT računa produktom {e(kT)+e[(k-1)T]}.(T/2)
Kod Tustinove ili bilinearne transformacije koristi se trapezno pravilo pa je aproksimacijski proračun integrala (3.4.23):
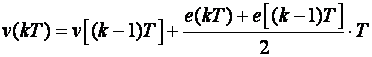
Prebacimo jednadžbu u z područje:
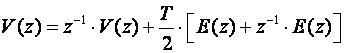(3.4.25)
Definirajmo fiktivnu impulsnu prijenosnu funkciju V(z)/E(z) i izračunajmo je iz jednadžbe (3.4.25):
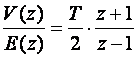(3.4.26)
Vratimo se sada ponovo na integral (3.4.23) i prebacimo ga u Laplaceovo područje:
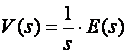(3.4.27)
Izračunajmo prijenosnu funkciju V(s)/E(s):
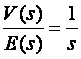(3.4.28)
Jednadžbe (3.4.28) i (3.4.26) odnose se na isti integral (3.4.23), pa se po Tustinovoj metodi može smatrati da 1/s odgovara (T/2).[(z+1)/(z-1)], odnosno da s odgovara (2/T).[(z-1)/(z+1)], te se W(z) može aproksimirati tako da se u W(s) svaki s zamjeni sa:
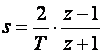(3.4.29)
(3.4.30)
Napomena: Tustinova aproksimacija se u stvari temelji na zamjeni s=(ln z)/T. Razvoj u red izraza (ln z)/T daje (2/T)[(z-1)/(z+1)+(z-1)3/3(z+1)3+...], pa se zamjena (3.4.29) sastoji od uzimanja samo prvog člana ovog razvoja.
Pogledajmo primjer:
Primjer:
Neka je W(s) isti kao u prethodnom primjeru
Lako je uočiti da se ovako dobiveni W(z) razlikuje od GE(z) dobivenog korištenjem tablica.
Napomena: Treba primijetiti da W(z) dobiven Tustinovom aproksimacijom uspoređujemo s GE(z), dakle sa Z - transformacijom serijskog spoja kontinuiranog sustava i sklopa za obnavljanje 0-tog reda, a ne sa G(z). Aproksimacijska metoda nastoji kontinuiranu funkciju prebaciti u diskretno područje što vjernije, bar što se tiče odziva, a to pretpostavlja realnu situaciju da je na ulazu kontinuiranog sustava kontinuiran (stepeničasti) signal a ne čisti diskretni signal. Usporedimo li odzive funkcije W(z) dobivene nekim od aproksimacijskih metoda i odzive funkcije G(z) dobivene Z transformacijom samog kontinuiranog sustava pojaviti će se razlika za konstantu pojačanja. O tome smo već prije govorili, ali ponovimo – u prvom slučaju se pretpostavlja da je na ulazu sustava stepeničasti signal (realna situacija), a u drugom da je diskretni signal (nerealna situacija). Ovu ćemo pojavu ilustrirati u drugom dijelu sljedećeg primjera.
Primjer:
Usporedimo najprije GE(z) dobiven korištenjem tablica (razvojem na parcijalne razlomke) i W(z) dobiven Tustinovom aproksimacijom za T=0.1 .
Razvoj na parcijalne razlomke i tablice daju
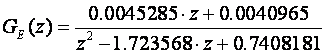
dok Tustinova metoda daje
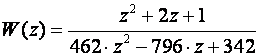
Na prvi pogled ogromna razlika, ali izračunamo li polove, u prvom slučaju polovi su p1=0.9072 i p2=0.8168, dok su u drugom slučaju za Tustinovu metodu p1=0.9047 i p2=0.8181, dakle skoro identični.
Još je zanimljivije pogledati odzive kontinuiranog sustava G(s) i odzive sustava diskretiziranog razvojem na parcijalne razlomke i Tustinovom aproksimacijom. Rezultat prikazuje slika 3.4.9 za T=0.1.
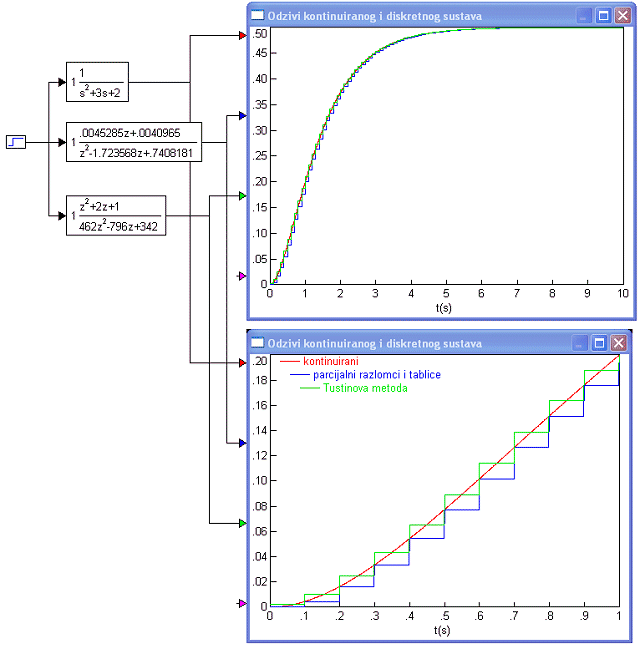
Slika 3.4.9. Odzivi kontinuiranog sustava i diskretnog sustava čija je impulsna prijenosna funkcija dobivena razvojem na parcijalne razlomke ekvivalentne prijenosne funkcije i Tustinovom aproksimacijom za T=0.1 (Tustinova.vsm )
Na slici se odlično vidi razlika u aproksimacijama. Tustinova metoda se temelji na trapeznom pravilu, pa se zato između dva perioda uzorkovanja signal zamjenjuje srednjom vrijednosti, dok se metoda diskretizacije ekvivalentne prijenosne funkcije temelji na unaprijednoj diferenciji i naziva se aproksimacija za skokoviti signal (to ćemo u nastavku ovog poglavlja i dodatno objasniti), pa zato signal između dva perioda uzorkovanja nadomješta njegovom vrijednošću na početku tog intervala.
Tustinova aproksimacija uvijek u brojniku sustava dodaje jedan član više u odnosu na razvoj na parcijalne razlomke (na slici 3.4.9 to je z2 u brojniku). Zbog toga se u frekvencijskim karakteristikama ova dva načina diskretizacije prijenosne funkcije pojavljaju razlike. Zanimljivu modifikaciju Tustinove metode kojom se uklanja ovaj problem i u brojniku dobije isti red kao kod razvoja na parcijalne razlomke, predložio je 1993. Janiszowski (K.B. Janiszowski, A Modification and the Tustin Approximation, IEEE Trans. on Automatic Control, Vol. 38, No. 8, pp. 1313-1316, 1993). Njegova se modifikacija sastoji u množenju W(z) sa faktorom 2/(z+1). Dodani faktor ne utječe na red prijenosne funkcije ni na faktor pojačanja, a eliminira dodani član u brojniku. Za prethodni primjer modificirana aproksimirana impulsna prijenosna funkcija bi bila:
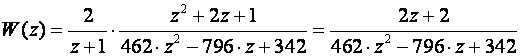
Odziv joj se u potpunosti poklapa s odzivom dobivenim za metodu razvoja na parcijalne razlomke i korištenje tablica.
Napomena: VisSim ima ugrađenu mogućnost prelaska iz opisa prijenosnom funkcijom u opis impulsnom prijenosnom funkcijom (Convert s ->z) uz definiranje perioda uzorkovanja koji se u VisSimu naziva dT:
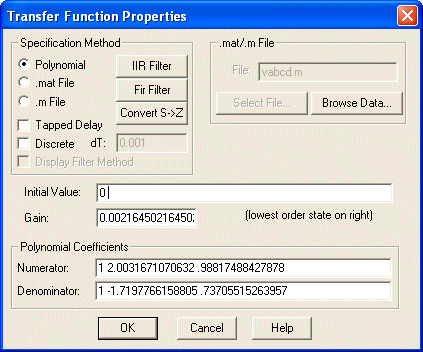
Na slici je dan rezultat za prijenosnu funkciju iz prethodnog primjera:
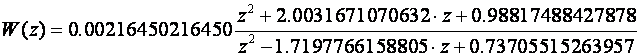
što je skoro identično s Tustinovom aproksimacijom ako iz nazivnika izlučimo 462:
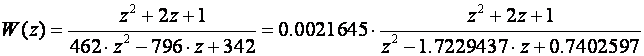
Eulerova aproksimacija
Osim Tustinove metode aproksimacije postoji i Eulerova metoda koja se temelji na unaprijednoj diferenciji, pa se jednadžba (3.4.24) piše u obliku:
(3.4.31)
iz čega dalje slijedi
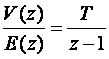(3.4.32)
odnosno
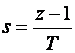(3.4.33)
Treća se aproksimacijska metoda temelji na povratnoj diferenciji. Jednadžba (3.4.24) sada glasi:
(3.4.34)
iz čega je lako dobiti
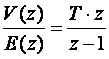(3.4.35)
pa je
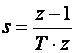(3.4.36)
Nedostatak Eulerove metode i metode temeljene na povratnoj diferenciji je taj što se sustavi koji su u kontinuiranom području stabilni mogu u diskretnom području preslikati kao nestabilni (Euler), odnosno sustavi koji su u kontinuiranom području nestabilni mogu se u diskretnom preslikati kao stabilni (povratna diferencija). Kod Tustinove metode informacija o stabilnosti je uvijek i u potpunosti sačuvana – sustav stabilan u kontinuiranom području biti će stabilan i u diskretnom i obrnuto, ali o tome više u poglavlju o vezi između s i z ravnine.
......................................................................
Problem svih aproksimacijskih metoda je i taj što se frekvencijska skala izobličuje. To može stvarati probleme posebno u realizaciji digitalnih filtra. Uzmimo jedan primjer. Projektiramo u kontinuiranom području pojasni propust, prebacimo ga Tustinovom metodom u z područje, realiziramo digitalni filter i njegov pojas propuštanja više nije tamo gdje smo ga projektirali. Frekvencija pojasnog propusta se pomakla, frekvencijska skala je izobličena. Englezi ovu pojavu zovu “frequency warping”. Rješenje je modificirana Tustinova aproksimacija kod koje je uvedena korekcija iskrivljenja frekvencijske skale (eng. Prewarping Correction):
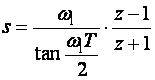(3.4.37)
Korekcija vrijedi samo za frekvenciju ω1. Na njoj će kontinuirani filter i aproksimirani diskretni filter imati istu vrijednost, međutim na drugim frekvencijama izobličenje će još uvijek postojati.
Aproksimacija za skokoviti signal
Vratimo se sada još jedan put na postupak kod kojeg smo računali GE(z) iz G(s) korištenjem tablica. Pretpostavimo li da je sklop za obnavljanje fiktivni, da fizički ne postoji više se ne radi o ekvivalentnom sustavu već o još jednoj aproksimacijskoj metodi prelaska iz s u z područje koja se naziva aproksimacija za skokoviti signal (eng. Step-invariance). Osnovna joj je pretpostavka prebaciti funkciju W(s) u z područje tako da im odziv za skokoviti signal budu što bliži. Ovo nam daje i malo drugačiji uvid u jednadžbu (3.4.21) pa ga je korisno detaljnije objasniti.
Pretpostavimo da smo na ulaz kontinuiranog sustava prijenosne funkcije W(s) doveli jedinični skokoviti signal x(t)=u(t). Laplaceova transformacija ovog signala je X(s)=1/s, a odziv sustava u Laplaceovom području računa se jednadžbom
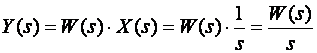(3.4.38a)
Pređimo sada u z područje i napravimo Z - transformaciju odziva Y(s)
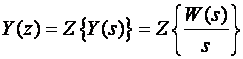(3.4.38b)
Kako je Y(z)=W(z).X(z), da bi odredili W(z) treba nam još i Z - transformacija signala koji smo doveli na ulaz sustava, a to je jedinični skok. Tablica na slici 3.3.1 daje X(z)=z/(z-1) pa dalje direktno slijedi:
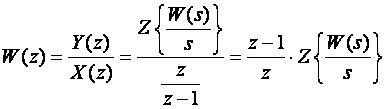(3.4.39)
a to je upravo jednadžba koju smo dobili kod proračuna impulsne prijenosne funkcije ekvivalentni sustava, s tim da smo tamo umjesto oznaka W(s) imali G(s), a umjesto W(z) imali smo GE(z).
Zaključimo – koristimo li kod aproksimacije impulsne prijenosne funkcije W(z) tablicu sa slike 3.4.6 odziv sustava će biti točan ukoliko mu se na ulaz dovede stepeničasti signal koji se mijenja samo u trenucima uzorkovanja, a između dva trenutka uzorkovanja je konstantan. Aproksimaciju možemo sažeto prikazati u tri koraka:
1. Proračunati odziv sustava Y(s)=W(s)X(s), prijenosne funkcije W(s) u s području ukoliko mu je na ulaz doveden jedinični skokoviti signal x(t)=u(t) čija je Laplaceova transformacija X(s)=1/s.
2. Odrediti Z transformaciju Y(z) odziva Y(s).
3. Podijeliti Y(z) sa Z - transformacijom linearnog ulaznog signala X(z)=z/(z-1)
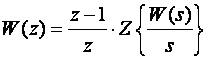(3.4.40)
Aproksimacija za pravčasti signal
Na sličan se način definira i aproksimacija za pravčasti signal (eng. Ramp-invariance) kod koje se nastoji da odziv sustava bude točan ukoliko se ulazni signal između dva trenutka uzorkovanja mijenja pravčasto (linearno uzlazno ili silazno). Postupak je u osnovi isti kao i prije samo što se sada na ulaz dovodi jedinični pravac x(t)=t. Ponovo ga izrazimo postupkom od tri koraka:
1. Proračunati odziv sustava Y(s)=W(s)X(s), prijenosne funkcije W(s) u s području ukoliko mu je na ulaz doveden jedinični uzlazni signal x(t)=t čija je Laplaceova transformacija X(s)=1/s2.
2. Odrediti Z - transformaciju Y(z) odziva Y(s).
3. Podijeliti Y(z) sa Z - transformacijom linearnog ulaznog signala X(z)=(Tz)/(z-1)2
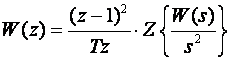(3.4.41)
Primjer
Odredi aproksimaciju za skokoviti signal i aproksimaciju za pravčasti signal ukoliko je sustav čisti integrator W(s) = 1/s .
Aproksimacija za skokoviti signal
1.
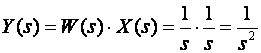
2.
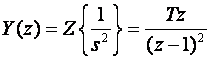
3.
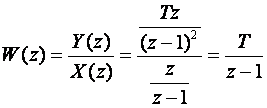
Aproksimacija za pravčasti signal
1.
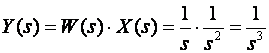
2. U tablici na slici 3.3.1 nismo naveli Z - transformaciju od 1/s3, ali je zato navodimo ovdje
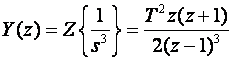
3.
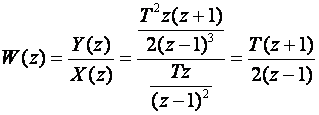
Zanimljivo je da aproksimacija prijenosne funkcije W(s)=1/s za skokoviti signal daje rezultat koji odgovara jednadžbi koja se koristi kod Eulerove aproksimacije, a aproksimacija za pravčasti signal jednadžbi kojom se 1/s zamjenjuje kod Tustinove aproksimacije. Ovdje leži i objašnjenje situacije na slici 3.4.8 kod koje se diskretizacija temeljena na razvoju ekvivalentne prijenosne funkcije na parcijalne razlomke ponaša kao aproksimacija temeljena na unaprijednoj diferenciji.