4.4.1.  Bilinearna transformacija

Osnovna ideja uvođenja bilinearne transformacije jest prebaciti se jednoznačno iz z područja u neko novo područje, na način da se jedinični krug z ravnine preslika u cijelu lijevu polu-ravninu tog novog područja. Prisjetimo se da Z - transformacija nije jednoznačna. Jedinični krug se preslika u lijevi dio osnovnog pojasa s ravnine (lijevi polu-pojas) i sve druge polu-pojaseve paralelne s njim, a cijela z ravnina se preslika u osnovni pojas s ravnine i sve pojaseve paralelne s njim. Zbog toga s teorijske točke gledanja nije moguće koristiti inverznu Z - transformaciju za vraćanje iz z područja u s područje. Treba nam nova transformacija i novo područje kod koje je preslikavanje jednoznačno. Napomenimo i to da s praktične točke gledanja vraćanje iz z ravnine u s ravninu i nije toliki problem zato što je frekvencija uzorkovanja obično toliko velika da se sve singularne točke nalaze unutar osnovnog pojasa (širinu osnovnog pojasa definira kružna frekvencija uzorkovanja ω_s pa što je frekvencija uzorkovanja veća to je i širina osnovnog pojasa veća), ali u svakom slučaju primjena bilinearne transformacije daje jednoznačno preslikavanje.

Najpogodnija transformacija za jednoznačno preslikavanje z ravnine je bilinearna transformacija ili kako se često zove linearna frakcionalna transformacija. Njezin opći oblik je

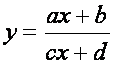      (4.4.8)

gdje su a, b, c i d konstante, a x i y varijable. U grupu bilinearnih transformacija spada na primjer translacija (y = ax + b) ili inverzija (y = 1/x), ali u diskretnim sustavima koristi se oblik kod koga su konstante su a = b = d = 1 i c = -1, dok se nova varijabla zove w i ona odgovara varijabli x, a varijabli y odgovara varijabla z, pa se veza između varijable z iz z ravnine i nove varijable w iz nove w ravnine definira izrazom

      (4.4.9)

Impulsna prijenosna funkcija G(z) iz z ravnine prebacuje se u oblik G(w) u w ravnini transformacijskom jednadžbom:

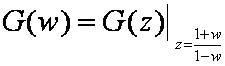      (4.4.10)

Varijabla w je također kompleksna varijabla w = u + jv isto kao što je i varijabla s kompleksna varijabla s = σ + jω. Pokušajmo povezati imaginarnu komponentu varijable w i imaginarnu komponentu varijable s. Izrazimo najprije w preko z:

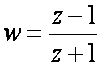      (4.4.11)

Uvrstimo li sada z=e^jωT dobijemo 

      (4.4.12)

pa slijedi da je

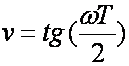      (4.4.13)

Što to znači? Jednadžba (4.4.13) daje vezu između s i w ravnine. Frekvencijski dijagrami w ravnine za promjenu varijable v od 0 do ∞, odgovaraju u s ravnini frekvencijskim dijagramima za promjenu frekvencije ω  od 0 do π/T. Zbog toga neki autori (C.L. Phillips, H.T. Nagle, Digital Control Systems Analysis and Design, Prentice-Hall, 1984) predlažu da se kod bilinearne transformacije koristi Tustinov oblik bilinearne transformacije:

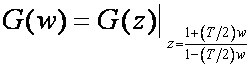      (4.4.14)

odnosno

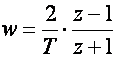      (4.4.15)

Izvede li se u ovom slučaju veza između v i ω dobije se:

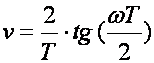      (4.4.16)

Za male vrijednosti perioda uzimanja uzoraka T, tangens je približno jednak kutu pa imamo v ≈ (2/T)^.(ωT/2), odnosno v ≈ ω. To znači da sve veličine vezane uz pseudo-frekvenciju v u w ravnini za male vrijednosti perioda uzorkovanja T odgovaraju frekvencijama ω koje bismo dobili da smo se iz inverznom Z - transformacijom iz z ravnine vratili natrag u s ravninu. Na primjer crtamo frekvencijske dijagrame diskretnog sustava drugog reda i u w ravnini dobijemo rezonantno nadvišenje na nekoj pseudo-frekvenciji v_R. Ukoliko je korištena bilinearna transformacija oblika (4.4.14) ta će pseudo-frekvencija brojčano približno odgovarati stvarnoj frekvenciji rezonantnog nadvišenja  ω_R ≈ v_R, a ukoliko je korištena bilinearna transformacija oblika (4.4.10) tada se stvarna frekvencija rezonantnog nadvišenja treba proračunati iz jednadžbe (4.4.13) izrazom ω_R= (2/T)^.arctg (v_R).

Ponekad se zbog toga i u nazivu pravi razlika, pa se transformacija tipa  (4.4.10) naziva Möbiusova bilinearna transformacija, a transformacija tipa  (4.4.14) Tustinova bilinearna transformacija.