4.4.2. Nyquistovi frekvencijski dijagrami
Nyquistov frekvencijski dijagram diskretnog sustava crtamo direktno tako da u G(z) napravimo zamjenu z=ejωT=ejω i mijenjamo ω od 0 do π. Pogledajmo primjer:
Primjer:
Nacrtaj Nyquistov frekvencijski dijagram za diskretni sustav ukoliko je
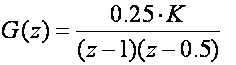, T = 0.1 i K = 1.
Napravimo zamjenu z=ejω pa dobijemo:
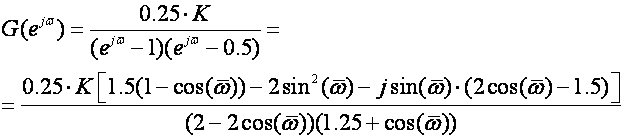
Sada bi još trebalo mijenjati ω od 0 do π i crtati frekvencijski dijagram. Dijagram za ω=0 počinje u trećem kvadrantu iz -∞ a završava ω=π na realnoj osi u točki 0.8333.
Slika 4.4.3 prikazuje dio Nyquistovog dijagrama oko ishodišta. Donja krivulja je polarna krivulja za pozitivne frekvencije, a gornju smo dobili zrcalnom slikom oko realne osi i ona predstavlja polarnu krivulju za fiktivne negativne frekvencije.
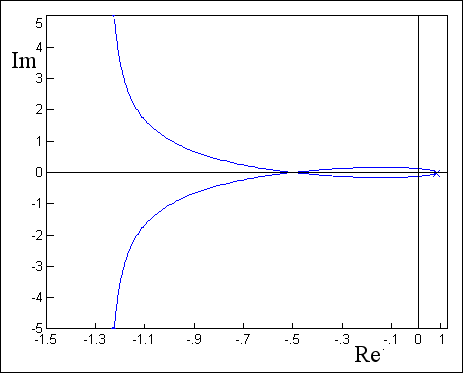
Slika 4.4.3. Nyquistov frekvencijski dijagram sustava impulsne prijenosne funkcije G(z) = 0.25/(z-1)(z-0.5)
Iz prethodnog je primjera jasno koliko je teško crtati Nyquistov dijagram bez dobrog CAD alata. VisSim ima takav alat, ali ne dopušta direktno crtanje već se treba najprije primijeniti bilinearna transformacija, te impulsnu prijenosnu funkciju promatrati u kontinuiranom w području. Pogledajmo ponovo prethodni primjer:
Primjer:
Nacrtaj Nyquistov frekvencijski dijagram za diskretni sustav ukoliko je
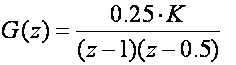, T = 0.1 i K = 1.
koristeći bilinearnu transformaciju.
Möbiusova bilinearna transformacija kod koje je z=(1+w)/(1-w) daje:
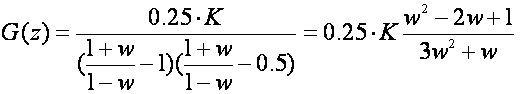
Slika 4.4.4 prikazuje rezultate VisSim simulacije. To što na modelu piše varijabla s nije važno, važno je da mi znamo da smo transformaciju primijenili.
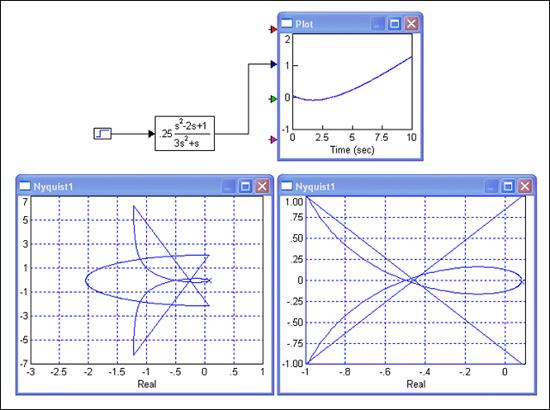
Slika 4.4.4. Nyquistov dijagram sustava nakon primjene bilinearne transformacije za K = 1.
Na Nyquistvom dijagramu vide se i neobične ravne linije koje ne pripadaju samom Nyquistovom dijagramu (dvije kose linije i poluelipsa). To su linije koje na simbolički način pokazuju da se Nyquistova krivulja zatvara u beskonačnosti. Njih jednostavno treba zanemariti, te ukoliko želimo analizirati stabilnost, trebamo promatrati zatvaranje Nyquistove krivulje na način opisan u sljedećem primjeru.
Pogledajmo što dobijemo za Tustinovu bilinearnu transformacije. Primjena jednadžbe (4.4.15) daje:
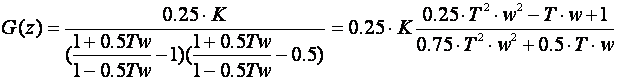
Pogledajmo rezultate za različiti period uzimanja uzoraka T:
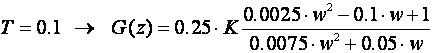
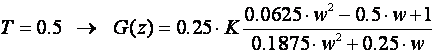
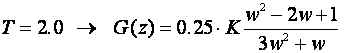
Za T = 2 oba se opisa podudaraju. Slika 4.4.5 prikazuje dio Nyquistovog dijagrama oko ishodišta za sve tri vrijednosti perioda uzorkovanja T.
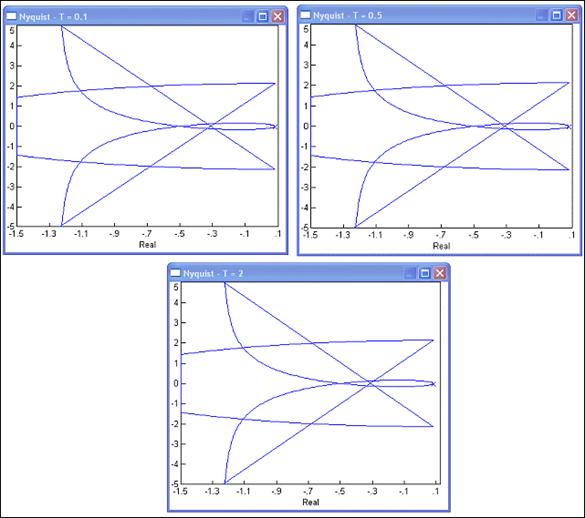
Slika 4.4.5. Nyquistov dijagram sustava nakon primjene drugog oblika bilinearne transformacije za K = 1 i različite vrijednosti perioda uzorkovanja T.
Razlike nije moguće uočiti, dijagrami su izgledom identični. Ono što je različito su frekvencije v na kojima se to događa. U sva tri slučaja imamo drugačije frekvencijsko skaliranje, pa bi se primjerice presjecište Nyquistovog dijagrama i realne osi (točka -0.5) u svakom slučaju dobilo za različitu vrijednost v koja bi se nakon odgovarajućeg frekvencijskog skaliranja (jednadžba (4.416) - v = (2/T).tg(ωT/2) ) prebacilo u istu frekvenciju ω. Ono u čemu se sve tri slažu je vrijednost za v → ∞ koja odgovara frekvenciji ω =π/T = ωS/2.
Nyquistovi frekvencijski dijagrami u praksi su, prije pojave dobrih CAD alata se koristili uglavnom za:
a) analizu stabilnosti zatvorenog regulacijskog sustava na temelju poznavanja prijenosne funkcije otvorene petlje,
b) analizu i projektiranje sustava koji će u zatvorenoj petlji imati odgovarajuće pojačanje M i fazni pomak N.
Danas u analizi diskretnih sustava Nyquistovi dijagrami nisu toliko značajni, a posebno projektiranje sustava vođenja temeljeno na pojačanju zatvorene petlje definiranom M kružnicama ili na faznom pomaku zatvorene petlje definirano N kružnicama, pa se ovdje s njima nećemo niti baviti. Kazati ćemo samo nekoliko riječi o analizi stabilnosti pomoću Nyquistovih frekvencijskih dijagrama.
Analiza stabilnosti pomoću Nyquistovih dijagrama
Diskretni zatvoreni regulacijski sustav čija impulsna prijenosna funkcija otvorene petlje nema polova izvan jedinične kružnice biti će stabilan ukoliko njena zatvorena Nyquistova krivulja ne obuhvaća točku -1 + j0.
Ukoliko postoje nestabilni polovi impulsne prijenosne funkcije otvorene petlje izvan jedinične kružnice, tada će zatvoreni diskretni regulacijski sustav biti stabilan ukoliko zatvorena Nyquistova krivulja obilazi u smjeru suprotnom od kazaljke sata točku -1 + j0 onoliko puta koliko postoji polova izvan jedinične kružnice
Zatvorena Nyquistova krivulja se dobije tako da se nacrta Nyquistov dijagram i njegova zrcalna slika, te se u beskonačnosti spoje s onoliko beskonačnih polukrugova kolika je vrst sustava (broj polova u z = 1). Pogledajmo prethodni primjer sa stajališta stabilnosti i još ga malo proširimo:
Primjer:
Impulsna prijenosna funkcija otvorenog sustava iz prethodnog primjera dobivena je serijskim spojem ekvivalentnog sustava čiji je kontinuirani dio G(s)=3.4657/(s+6.9314) i digitalnog regulatora impulsne prijenosne funkcije Gc(z)=K/(z-1). Slika 4.4.6 prikazuje sustav za K=1 i T=0.1. Izvede li se GE(z), dobije se GE(z) = 0.25/(z-0.5), pa je serijski spoj ova dva bloka upravo impulsna prijenosna funkcija iz prethodnog primjera.
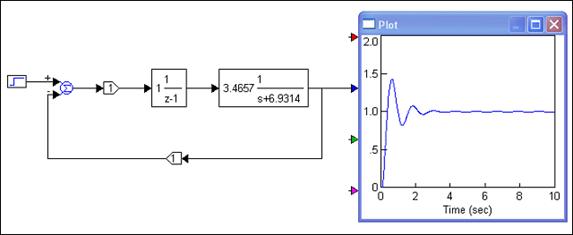
Slika 4.4.6. Diskretni regulacijski sustav (T = 0.1 i K = 1)(vissim/stabilnost_1.vsm)
Sa slike je očito da je za K = 1 zatvoreni regulacijski sustav stabilan. Pitanje je do koje vrijednosti konstante pojačanja K će sustav ostati stabilan? Koliko je njegovo kritično pojačanje nakon kojeg prelazi u nestabilno područje?
Odgovor daje Nyquistov dijagram koji smo prikazali na slici 4.4.3 i VisSimova verzija na slici 4.4.4. Ovdje ćemo ga dati u dopunjenom obliku, dodavanjem polukružnica u beskonačnosti:
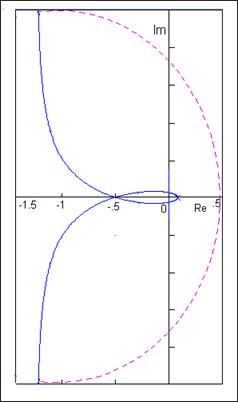
Slika 4.4.7. Nyquistov dijagram impulsne prijenosne funkcije otvorene petlje sustava sa slike 4.4.6
Sustav je stabilan, kako smo i zaključili iz njegovog vremenskog odziva, zato što impulsna prijenosna funkcija nema polova izvan jedinične kružnice, a zatvorena Nyquistova krivulja ne obilazi točku -1+j0. Granica stabilnosti je kada Nyquistov dijagram upravo prolazi kroz točku -1+j0, a to će se dogoditi ukoliko udvostručimo konstantu pojačanja K. Dakle odgovor je: sustav će biti stabilan dok je K < 2. Slika 4.4.8 prikazuje odziv sustava za K = 2. Odziv je oscilatorni.
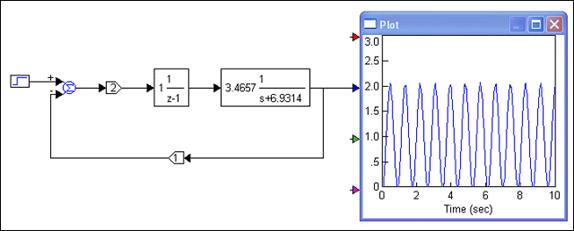
Slika 4.4.8. Diskretni regulacijski sustav (T = 0.1 i K = 2)
Pogledajmo još jedan primjer.
Primjer
Odredi stabilnost diskretnog sustava sa slike 4.4.9.
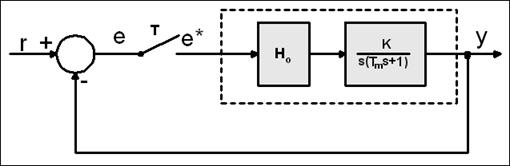
Slika 4.4.9. Diskretni regulacijski sustav
Kontinuirani dio je istosmjerni motor kod kojeg je zanemareno trenje u ležajevima i induktivitet namota. Impulsna prijenosna funkcija otvorene petlje je:
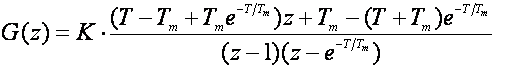
Za T = Tm = 1 dobije se
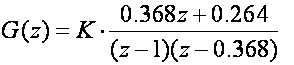
Naglasimo da ovo nije realna situacija i da je navodimo samo kao ilustraciju Nyquistovog kriterija stabilnosti. Nije realna zbog dva razloga. Prvi je taj što ubacivati u sustav sklop za uzorkovanje i odmah poslije njega sklop za obnavljanje nema nikakvog smisla. Između njih treba postojati bar nekakav diskretni regulator što je bio slučaj u prošlom primjeru. Drugi razlog je taj što smo uzeli period uzimanja uzoraka jednak vremenskoj konstanti sustava. On naravno treba biti puno manji. Međutim za početak analizirat ćemo stabilnost baš takvog sustava. Kako bi analizirali utjecaj pojačanja K impulsnu prijenosnu funkciju sustava skalirati ćemo konstantom pojačanja K:
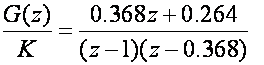
Primijenimo Möbiusovu bilinearnu transformaciju:
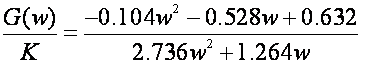
i nacrtajmo Nyquistov dijagram.
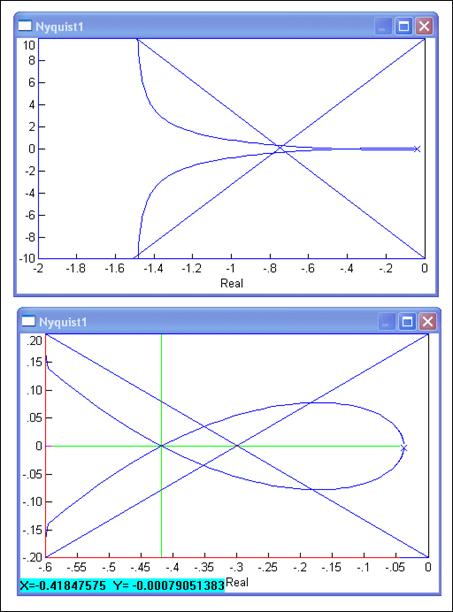
Slika 4.4.10. Nyquistov dijagram diskretnog regulacijskog sustava (stabilnost_2.vsm)
Na donjoj slici je povećan dio oko ishodišta. Nyquistov dijagram siječe realnu os u točki – 0.418. Prebacimo li ponovo pojačanje K na desnu stranu dobijemo uvjet granice stabilnosti 0.418.K≤1 iz čega slijedi da će sustav biti stabilan za K≤1/0.418=2.392.
Proračunajte kao vježbu za koje vrijednosti pojačanja K će sustav biti stabilan ukoliko je Tm = 1, a T = 0.1 .
Napomena: Kod ovog je primjera zanimljivo napomenuti da bi u slučaju uklanjanja diskretnih komponenata (sklopa za uzorkovanje i sklopa za obnavljanje) kontinuirani sustav imao prijenosnu funkciju otvorene petlje G(s)=K/s(Tms+1), pa bi bio strukturno stabilan za sve vrijednosti pojačanja K, dok je diskretni sustav stabilan samo za K manji od 2.392. Znači diskretizacijom sustava mi smo strukturno stabilan sustav učinili relativno stabilnim.
Nyquistovi dijagrami su zanimljivi i zbog toga što se na njima mogu odrediti i mjere relativne stabilnosti – amplitudna pričuva i fazna pričuva (vidi Definicije – Specifikacija odziva u frekvencijskom području). Amplitudna pričuva se definira na frekvenciji kod koje je faza prijenosne funkcije -180o. To je upravo u točki gdje Nyquistova krivulja siječe realnu os. Fazna pričuva se definira na frekvenciji gdje je amplituda sustava jedinična, a to je u točki gdje se Nyquistova krivulja i jedinična kružnica sijeku. Pogledajmo na primjeru Nyquistovog dijagrama sa slike 4.4.7.
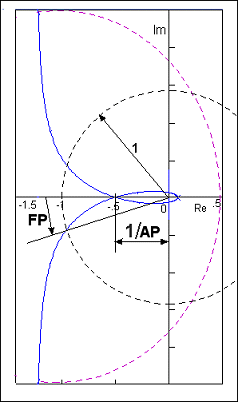
Slika 4.4.11. Uz definiciju amplitudne i fazne pričuve
Amplitudna pričuva je jednaka recipročnoj apsolutnoj vrijednosti udaljenosti od ishodišta do točke gdje Nyquistova krivulja siječe realnu os. U slučaju sa slike 4.4.11 iznositi će AP = 1/0.5 = 2. Za primjer sa slike 4.4.9 i K=1 biti će AP = 1/|-0.418| =1/0.418 = 2,392, a za K=1.5 AP=1/1.5*0.418=1/0.627=1.595. Ukoliko je izražavamo u decibelima, za prethodni primjer će biti za K=1 APdB=20 log 2,392 = 7.6 dB, a za K=1.5 APdB=20 log 1.595= 4.06 dB.
Faznu je pričuvu na slici teže odrediti i trebalo bi je računati.
Sa slike je uočljivo i to da je za stabilne sustave kod kojih impulsna prijenosna funkcija otvorene petlje nema polove izvan jedinične kružnice, frekvencija kritične (jedinične) amplitude uvijek manja od frekvencije kritične faze (ωI<ωπ).