4.4.3. Bodeovi frekvencijski dijagrami
Bodeovi frekvencijski dijagrami diskretnih sustava crtaju se tako da se na impulsnu prijenosnu funkciju najprije primjeni bilinearna transformacija, a onda je postupak isti kao da se crtaju Bodeovi dijagrami kontinuiranih sustava. Korisni su zbog toga što je na njima jednostavno uočiti značajke ponašanja sustava u frekvencijskom području. Na njima se direktno očitava amplitudna i fazna pričuva, uoči rezonantno nadvišenje, izračuna pojas propuštanja itd. (vidi Definicije – Specifikacija odziva u frekvencijskom području).
U analizi kontinuiranih sustava detaljno je razrađen postupak brzog crtanja Bodeovih dijagrama faktorizacijom brojnika i nazivnika prijenosne funkcije i zamjenom s=jω. Postupak je isti i za diskretne sustave s tim da se primjenjuje na prijenosnu funkciju G(w) uz zamjenu w=jv. Pri tome se javljaju dva problema:
a) Ukoliko koristimo bilinearnu transformaciju oblika z=(1+w)/(1-w) javlja se frekvencijsko izobličenje. Frekvencije na tako dobivenoj slici i stvarne frekvencije vezane su izrazom v=tg(ωT/2) o čemu treba voditi računa. Koristi li se Tustinov oblik z=(1+0.5Tw)/(1-0.5Tw) veza između frekvencija je v=(2/T).tg(ωT/2), pa se bar za male frekvencije i periode uzorkovanja tangens može približno zamijeniti svojim argumentom te će v ≈ ω. U svakom slučaju u ovome treba voditi računa na primjer kod proračuna pojasa propuštanja ili određivanja frekvencije rezonantnog nadvišenja. Iz vrijednosti dobivene sa Bodeovih dijagrama treba se proračunati stvarna vrijednost frekvencije ovisno o tome koju smo bilinearnu transformaciju koristili.
b) U prijenosnoj funkciji G(jv) često se jave faktori ne-minimalne faze oblika (1-jvτ), τ >0,što donosi probleme kod crtanja na način da se fazna karakteristika crta obrnuto od fazne karakteristike oblika (1+jvτ), τ >0. To znači ukoliko je (1-jvτ), τ >0 u brojniku njegova će faza padati od 0o do -90o, a ukoliko je u nazivniku rasti od 0o do 90o . Posljedica toga je da na primjer CAD podrška VisSima za crtanje faznih karakteristika daje faznu karakteristiku translatiranu prema pozitivnim vrijednostima. Ilustrirajmo to jednim primjerom.
Primjer:
Analizirajmo sustav sa slike 4.4.9 s tim da ćemo uzeti realniju situaciju Tm = 0.5, T = 0.1 i K = 750.
Impulsna prijenosna funkcija ekvivalentnog sustava je
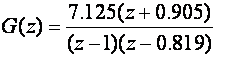
Möbiusova bilinearna transformacija kod koje je z=(1+w)/(1-w) daje
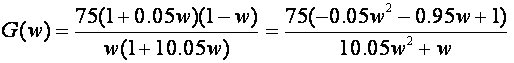
Slika 4.4.12 prikazuje Bodeove frekvencijske dijagrame dobivene simulacijskim programom VisSim.
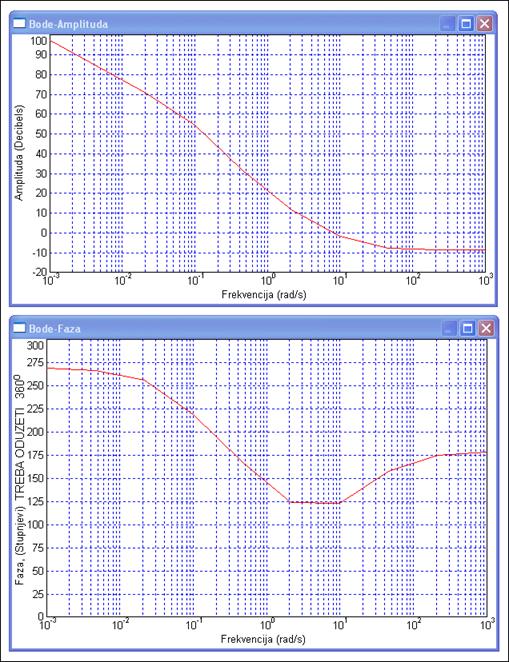
Slika 4.4.12. Bodeovi frekvencijski dijagrami za sustav sa slike 4.4.9 nakon primjene blinearne transformacije dobiveni VisSimom (fazni kut je zbog postojanja faktora ne-minimalne faze translatiran prema pozitivnim vrijednostima za 360o
Koje su stvarne vrijednosti kuta za velike i za male frekvencije dobijemo približnim računom:
Prijenosna funkcija u w području ima četiri faktora, dva u nazivniku, dva u brojniku, od kojih je jedan u brojniku ne-minimalne faze. Na malim frekvencijama faktor 1/w pridonosi sa -90o, a ostali faktori kutom od 0 o. Na velikim frekvencijama faktor 1/w i dalje pridonosi sa -90o, faktor 1/(1+10.05w) sa daljnjih sa -90o, faktor (1+0.05w) sa 90o i faktor ne-minimalne faze u brojniku sa -90o, znači sve skupa -180o. Na slici 4.4.12 na malim frekvencijama imamo 270o, a na velikim 180o, pa je očito da od vrijednosti faze dobivene na slici trebamo odbiti 360 o kako bi dobili stvarne vrijednosti.
Bodeovi dijagrami su posebno pogodni za utvrđivanje apsolutne i relativne stabilnosti u vidu amplitudne i fazne pričuve. Apsolutnu stabilnost utvrdimo odmah iz odnosa frekvencije na kojoj je (prava) faza –180o (vπ) i frekvencije na kojoj je amplituda 0 dB (vI). Za stabilan sustav treba biti vI manje od vπ. Relativnu stabilnost određujemo koristeći opciju 'Read coordinate' Vissima. Najprije očitamo vrijednost frekvencije na kojoj je faza -180 + korekcija zbog faktora ne-minimalne faze, pa onda na amplitudnom dijagramu pročitamo pripadnu vrijednost amplitude. Ona odgovara negativnoj vrijednosti amplitudne pričuve u dB (zato što je AP apsolutno jednak recipročnoj vrijednosti ove amplitude, a log recipročne vrijednosti je minus logaritam same vrijednosti)). Kod fazne pričuve je postupak obrnut, na amplitudnom dijagramu pročitamo frekvenciju na kojoj je amplituda 0 db (apsolutno jednaka 1), te na faznom dijagramu za tu frekvenciju očitamo vrijednost faze. Fazna pričuva je očitani kut + 180o –potrebna korekcija zbog faktora neminimalne faze.
Na prethodnom primjeru to izgleda ovako (vidi sliku 4.4.13):
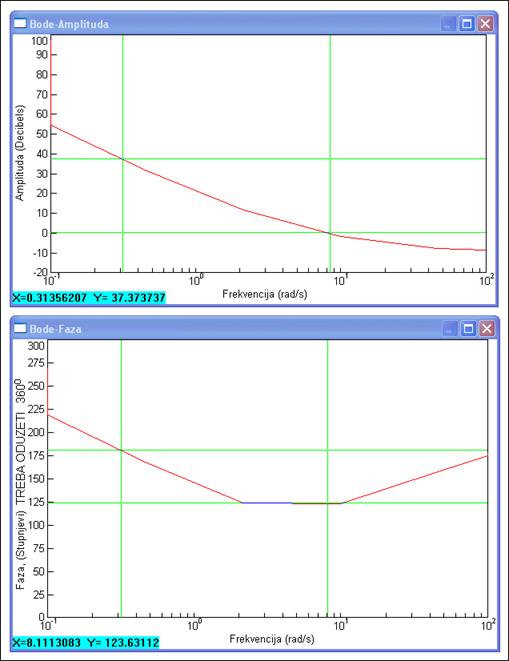
Slika 4.4.13. Amplitudna i fazna pričuva za prethodni primjer
Prvo zapažanje je da je sustav nestabilan.vI=8.11 rad/s, a vπ=0.314 rad/s, pa je očito da je vI veće od vπ i da je sustav nestabilan. Amplitudnu i faznu pričuvu je u tom slučaju bespotrebno računati iako i nju sa slike možemo pročitati: AP = -37.37 dB i FP = 123.63 o – 360 o + 180 o = -56.37 o.
Ovdje je zanimljivo i pokazati utjecaj frekvencijskog skaliranja. Sa slike smo očitali vI=8.11 rad/s. Stvarna frekvencija ωI izračuna se primjenom jednadžbe v=tg(ωT/2) iz koje izlazi ω=(2/T)arctg(v) pa u našem primjeru za T = 0.1 imamo ωI=(2/0.1)arctg(8.11)=28.96 rad/s.
Pogledajmo još jedan primjer stabilnog sustava. Neka to bude sustav sa slike 4.4.9 za koji smo već izračunali AP u poglavlju o Nyquistovim dijagramima.
Primjer:
Za sustav sa slike 4.4.9 te K=1 i T=1, prijenosna funkcija nakon primjene Möbiusove bilinearne transformacije z=(1+w)/(1-w) je:
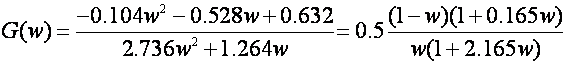
Sustav opet ima u brojniku jedan faktor neminimalne faze, pa će faza ponovo biti translatirana prema pozitivnim vrijednostima za 360o. Bodeove dijagrame prikazuje slika 4.4.14.
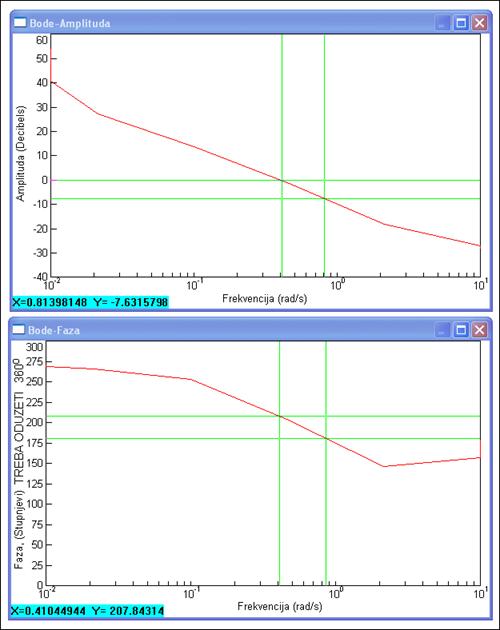
Slika 4.4.14. Bodeovi dijagrami istosmjernog motora sa slike 4.4.9 (stabilnost_2.vsm)
Sa slike čitamo vπ=0.814 rad/s i AP = - (-7.63 dB) = 7.63 db. Upravo onoliko koliko smo i prije izračunali. Kod fazne pričuve vI=0.41 rad/s i FP = 207.84o – 360 o+180 o = 27.84o. Zanima li nas primjerice stvarna frekvencija kritične faze dobijemo je iz jednadžbe ωπ=(2/0.1)arctg(0.814)=13.66rad/s.