Digitalno vođenje on-line (FESB, Split)

4.5. Geometrijsko mjesto korijena diskretnih sustava

Cilj: Naučiti kako se crta geometrijsko mjesto korijena diskretnih sustava i primjenjuje u analizi svojstava diskretnog sustava.

Geometrijsko mjesto korijena je hodograf polova prijenosne funkcije zatvorenog regulacijskog kruga za promjenu pojačanja sustava od 0 do beskonačno. Identična se definicija odnosi i na diskretne sustave. Pretpostavimo da imamo diskretni regulacijski sustav s negativnom povratnom vezom prikazan slikom 4.5.1.

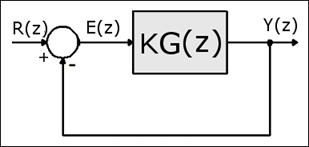
Slika 4.5.1. Diskretni regulacijski sustav

K je konstanta pojačanja. Impulsna prijenosna funkcija zatvorene petlje je

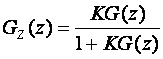(4.5.1)

Geometrijsko mjesto korijena daje vrijednosti polova impulsne prijenosne funkcije G_Z(z) za promjenu 0 ≤ K ≤ ∞. Crta se na isti način kao kod kontinuiranih sustava. U z ravnini ucrtaju se polovi i nule impulsne prijenosne funkcije otvorene petlje G(z), primjene se odgovarajuća pravila crtanja i dobije se geometrijsko mjesto korijena impulsne prijenosne funkcije (4.5.1). Naravno da će oblici GMK kod diskretnih sustava biti različiti od tipičnih oblika GMK kontinuiranih sustava, a vezano s tim i izvedeni zaključci će biti drugačiji - na primjer zaključak o stabilnosti. Kod kontinuiranih sustava sustav je asimptotski stabilan za sve vrijednosti pojačanja K za koje je GMK na lijevoj strani s ravnine. Kod diskretnih sustava je stabilan za sve vrijednosti pojačanja K za koje su polovi unutar jedinične kružnice.

Pogledajmo primjer.

Primjer:

Neka je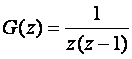

Nacrtaj GMK na duži način tako da se riješi karakteristična jednadžba.

Impulsna prijenosna funkcija zatvorenog sustava je

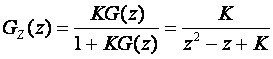
pa je karakteristična jednadžba z²-z+K=0, a njena rješenja

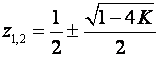
Polovi će biti realni za K ≤ 1/4. Za K > 1/4 polovi postaju konjugirano kompleksni

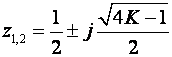
znači uvijek imaju istu realnu vrijednost 0.5 i za za K →∞ teže u beskonačnost prema vrijednosti 0.5 ± j∞.

Slika 4.5.2 prikazuje geometrijsko mjesto korijena ovog primjera. GMK izlazi izvan jediničnog kruga za pojačanje K veće od 1.

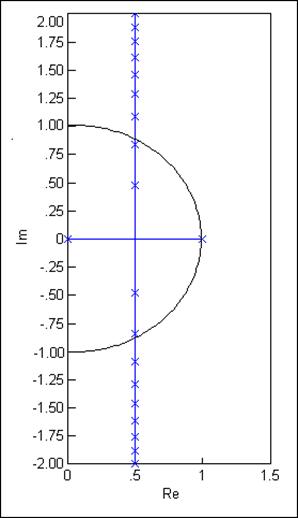
Slika 4.5.2. Geometrijsko mjesto korijena sustava impulsne prijenosne funkcije otvorene petlje G(z)=1/z(z-1)

Napomena: Sustav impulsne prijenosne funkcije G(z) = 1/(z(z-1)) ima jedan pol u točki z = 1 i jedan pol u točki z = 0, pa bi njemu odgovarao kontinuirani sustav čija prijenosna funkcija G(s) ima jedan pol u točki s = 0 i jedan pol u točki s = - ∞, što nije realna prijenosna funkcija i realan kontinuirani sustav drugog reda. Da impulsna prijenosna funkcija G(z) nije imala pol u točki z = 0 već na primjer u točki z = 0.5 (G(z) = 1/((z-0.5)(z-1)), onda bi se radilo o realnom kontinuiranom sustavu 2 reda s polovima u točkama s = 0 i s = (ln (0.5))/T). Vratimo se međutim na situaciju impulsne prijenosne funkcije G(z) = 1/(z(z-1)) i promotrimo je kao serijski spoj dvije impulsne prijenosne funkcije G(z) = (1/z) ^. (1/(z-1)). Drugi dio (1/(z-1)) odgovara ekvivalentnoj impulsnoj prijenosnoj funkciji čistog integratora prijenosne funkcije (1/s) za perid uzorkovanja T = 1. Za naki drugi period uzorkovanja T ekvivalentna impulsna prijenosna funkcija bi bila (1/T)(T/(z-1)). Prvi dio je u biti sklop za kašnjenje 1/z = z^-1. Prema ovome, ako na ulaz sustava impulsne prijenosne funkcije G(z) = 1/(z(z-1)) dovedemo neki ulazni signal on će najprije biti zakašnjen za 1 diskretni trenutak, a nakon toga propušten kroz integrator. Slika prikazuje primjer kod kojeg smo isti skokoviti signal doveli na ulaz sustava G(z) = 1/(z(z-1)) i sustava G(z) = 1/(z-1) za T = 1. Odzivi oba sustava su isti (integracijski) s tim da kod sustava G(z) = 1/(z(z-1)) odziv kasni jedan diskretni trenutak vremena, pa je i sustav impulsne prijenosne funkcije G(z) = 1/(z(z-1)) također realni sustav iako nema odgovarajuću realni prijenosnu funkciju G(s).

Slika uz napomenu: Odzivi sustava impulsnih prijenosnih funkcija G(z) = 1/(z(z-1)) i G(z) = 1/(z-1) za T = 1. Sustav G(z) = 1/(z(z-1)) samo uvodi kašnjenje za jedan diskretni trenutak vremena.

U nastavku ćemo ukratko ponoviti osnovna pravila za crtanje GMK, a nakon toga pokazati kako se GMK može crtati pomoću simulacijskog programa VisSim.

Pravila za crtanje GMK

Neka je G(z) impulsne prijenosne funkcije otvorene petlje koja ima n polova i m nula:

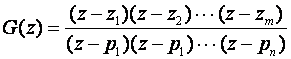(4.5.5)

Geometrijsko mjesto korijena (GMK) crta se korištenjem sljedećih pravila:

1. GMK ima n grana. Grane GMK su simetrične u odnosu na realnu os.

2. Grane počinju (K=0) u polovima impulsne prijenosne funkcije otvorene petlje i završavaju (K →∞) u nulama impulsne prijenosne funkcije otvorene petlje ili ukoliko ima više polova od nula, preostale grane koje ne završavaju u nulama završavaju u beskonačnosti.

3. Segmenti na realnoj osi koji leže lijevo od neparnog broja nula i/ili polova pripadaju GMK.

4. Grane koje ne završavaju u nulama asimptotski teže u beskonačnost. Asimptota ima P-N i sve sijeku realnu os u točki koja se naziva centroid i računa jednadžbom

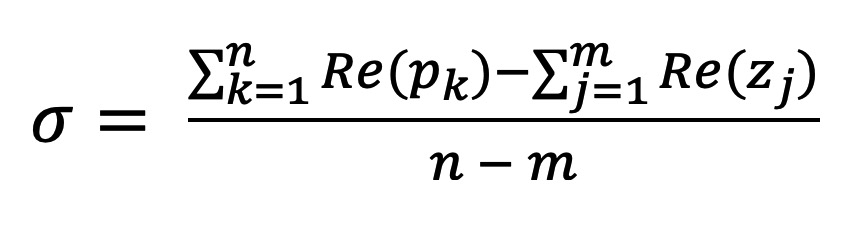(4.5.3)
gdje je Re() realni dio polova i nula.

Asimptote s realnom osi zatvaraju kutove

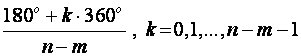(4.5.4)
Ovaj dio možemo interpretirati tako da kažemo da asimptote dijele s ravninu na onoliko jednakih dijelova koliko ima asimptota, a uz to trebaju biti i simetrične u odnosu na realnu os. Ako imamo jednu asimptotu ona će biti pod kutom od 180⁰ u odnsu na realnu os, što znači da će se poklapati s njom. U slučaju dvije asimptote one će biti pod kutevima +90⁰ i -90⁰ . U slučaju tri asimptote, dvije će biti pod kutevima +60⁰ i -60⁰ , a treća pod kutom od 180⁰.

5. Točka u kojoj GMK napušta realnu os naziva se točka izlaznog loma, a točka gdje GMK uzazi na realnu os naziva se točka ulaznog loima. Obje se računaju se kao ekstrem funkcije G(z) ili ekstrem funkcije K(z) = -1/G(z) uz uvjet da leži na GMK što znači da zadovoljavaju karakterističnu jednadžbu 1 + K G(z) = 0. Točeke izlaznog i ulaznog loma računaju se jednadžbama:

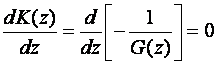(4.5.4)

ili

dG(z)/dz = 0 (4.5.4a)

Uzimaju se sam rješenja koja zadovoljavaju pravilo 3 (leže na GMK). Konjigirano kompleksna rješenja znače da nema točaka izlaznog/ulaznog loma.

6. Pojačanje K u bilo kojoj točki z_o GMK računa se izrazom

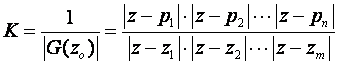(4.5.5)

Ako nema nula u nazivniku dolazi 1. Jednadžba (4.5.5) naziva se jednadžba modula.

7. Svaka točka z_o na GMK zadovoljava i jednadžbu argumenta koja kaže da je razlika između sume argumenata vektora povučenih iz svih nula od G(z) prema točki z_o i sume argumenata vektora povučenih iz svih polova od G(z) prema točki z_o jednaka 180^o+k 360^o gdje k može biti 0,1, 2, ...

8. Vrijednost kritičnog pojačanja K_KR i kružne frekvencije neprigušenih oscilacija ω_n koje odgovaraju točki u kojoj GMK presijeca jediničnu kružnicu i prelazi u područje nestabilnosti određuju se iz karakteristične jednadžbe 1+KG(z)=0 zamjenom z=e^-j^ω^T i izjednačenjem realnog i imaginarnog dijela s nulom.Kritično pojačanje se može izračunati i jednadžbom modula u točkama gdje GMK presjeca jediničnu kružnicu.

Pogledajmo primjenu pravila na jednom primjeru:

Primjer:

Nacrtaj GMK sustava sa slike 4.4.9 za T = T_m = 1 (za njega smo crtali i Nyquistove dijagrame). Impulsna prijenosna funkcija ekvivalentnog sustava je:

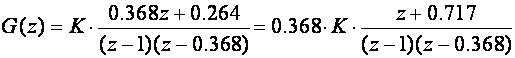
1. GMK ima 2 grane.

2. Grane polaze iz polova z=1 i z=0.368 i završavaju jedna u nuli z=-0.717 a druga u beskonačnosti.

3. Na realnoj osi GMK leži između točaka z=1 i z=0.368, te lijevo od točke z=-0.717.

4. Postoji jedna asimptota pod kutom od - 180^o, pa centroid nema smisla.

5. Točka u kojoj GMK napušta realnu os računa se iz jednadžbe

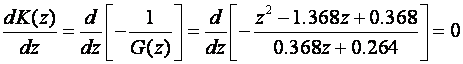
koja nakon derivacije u brojniku daje:

-((2z - 1.368)(0.368z+0.264) - 0.368 (z² - 1.368z + 0.368)) = -(0.736z² - 0.503z + 0.528z - 0.361 - 0.368z² + 0.503z - 0.135) = - (0.368 z² + 0.528z - 0.496) = - z² - 1.434z + 1.349 = 0

i nakon sređivanja dobijemo:

Rješenja jednadžbe su z₁ = 0.648 i z₂ = -2.082. Obje točke leže na GMK s tim da će z₁ = 0.648 biti točka izlaznog loma, a z₂ = -2.082 točka ulaznog loma.

Isti rezultat daje i derivacija dG(z)/dz koja u brojniku ima :

0.368 (z² - 1.368z + 0.368) - (2z - 1.368)(0.368z+0.264)= z² + 1.434z - 1.349 = 0

9. Pojačanje za koje GMK presijeca jediničnu kružnicu računa se iz karakteristične jednadžbe

uz zamjenu :

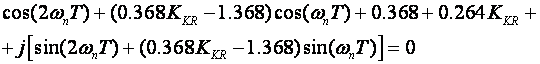
iz čega dobijemo dvije jednadžbe izjednačavajući realni i imaginarni dio s nulom. Rješenje je K_KR = 2.39 i ω_nT = 1.32rad. Kako je T = 1 frekvencija neprigušenih oscilacija je ω_n = 1.32rad/sek.

Točke u kojima GMK siječe jediničnu kružnicu su

Provjerimo K_KR koristeći jednadžbu modula:

iz čega slijedi

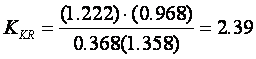
(Napomena: Vrijednost K=2.392 dobili smo i korištenjem Nyquistovih dijagrama. Za vježbu provjerite ove vrijednosti koristeći i Juryjev test stabilnosti).

I na kraju možemo skicirati GMK. Mi ćemo ipak u crtanju koristiti VisSim. Slično kao i kod bilinearne transformacije impulsna prijenosna funkcija se zadaje kao kontinuirana pazeći da sve predznake dobro unesemo. To što na dijagramu piše varijabla s umjesto z nam ne smeta. Bitno je da znamo što smo zadali. Slika 4.5.3 prikazuje VisSim model i dobiveni GMK.

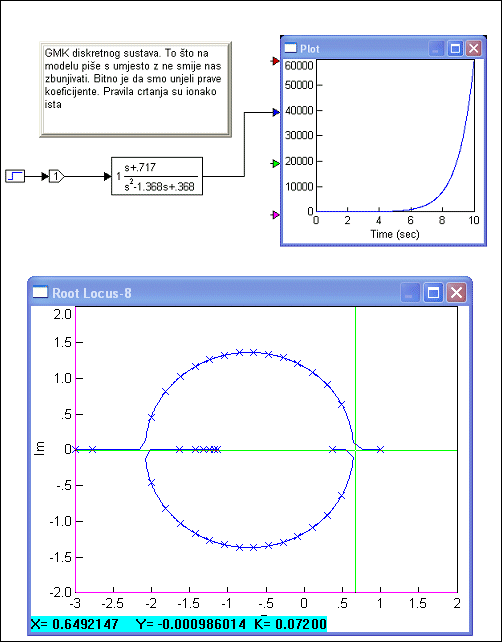
Slika 4.5.3. GMK iz prethodnog primjera za impulsnu prijenosnu funkciju otvorene petlje G(z)=(z+0.717)/(z-1)(z-0.368) (gmk_1.vsm)

Napomena uz sliku: Prije svega treba primijetiti da GMK na slici ne završava u nulama impulsne prijenosne funkcije otvorene petlje (jedna od nula je u točki -0.717, pa bi desna grana GMK trebala završiti u toj točki). Razlog je taj što se u VisSimu GMK računa za promjenu pojačanja od nule do neke maksimalne vrijednosti. Za primjer sa slike maksimalno pojačanje je bilo 100. Povećavanjem vrijednosti maksimalnog pojačanja točke poniranja GMK se približavaju nulama impulsne prijenosne funkcije otvorene petlje.

Na slici se vidi i pojačanje u točki izlaznog loma. Pri tome se ne smije zaboraviti da je očitana vrijednost 0.368K = 0.072, pa je stvarna vrijednost pojačanja K=0.072/0.368=0.196. (Napomena:Provjerite to analitički pomoću jednadžbe modula).

Nedostatak VisSima je što ne ucrtava jediničnu kružnicu, pa je do kritičnog pojačanja teže doći. Slika bi bila potpuna i puno jasnija uz jediničnu kružnicu. Ucrtamo li je u programu za crtanje dobiti ćemo sliku 4.5.4.

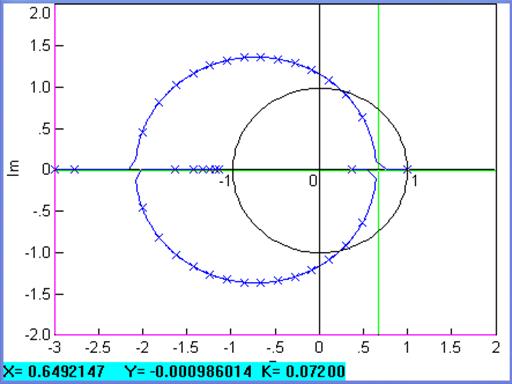
Slika 4.5.4. GMK iz prethodnog primjera s ucrtanom jediničnom kružnicom

Markeri na slici odgovaraju koraku povećanja pojačanja za približno 0.4. GMK presijeca jediničnu kružnicu malo iznad drugog markera iz čega slijedi da će približno biti 0.368^.K≈0.9 iz čega slijedi da je K≈2.4, znači približno koliko smo dobili i računski.

Na gornjem dijelu slike 4.5.3 je blok koji smo formirali da bi mogli nacrtati GMK. Vrijednosti odgovaraju impulsnoj prijenosnoj funkciji iako piše s a ne z. To trebamo zanemariti, GMK se dobro crta. Prikaz izlaznog signala otvorenog sustava nam nije bitan, ali ga VisSim zahtjeva da bi mogao nacrtati GMK.

Kazali smo da je zatvoreni diskretni regulacijski sustav nestabilan za one vrijednosti pojačanja K za koje GMK izlazi izvan jedinične kružnice. A što je s polovima unutar jedinične kružnice? Njihov se položaj obično vezuje sa stupnjem prigušenja ζ i frekvencijom neprigušenih oscilacija ω_n. Položaj kompleksnih polovi unutar jedinične kružnice koji imaju konstantni ζ i konstantan ω_n prikazan je na slici 4.5.5. ω_nje iskazan kao funkcija kružne frekvencije uzimanja uzoraka ω_S .

Superponiramo li ove krivulje na GMK za svako pojačanje K možemo ustanoviti koliki je stupanj prigušenja i frekvencija neprigušenih oscilacija, a iz njih možemo proračunati sve značajke vremenskog odziva (vidi Definicije – Specifikacija odziva u vremenskoj domeni)

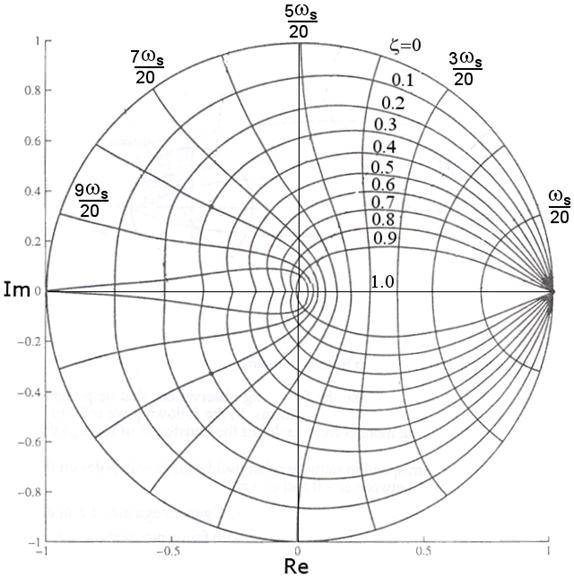
Slika 4.5.5. Krivulje konstantnog stupnja prigušenja ζ i frekvencije neprigušenih oscilacija ω_n iskazane kao funkcija kružne frekvencije uzimanja uzoraka ω_S nacrtane unutar jedinične kružnice

Povežimo krivulje konstantnog stupnja prigušenja ζ i frekvencije neprigušenih oscilacija ω_n

Primjer:

Superponiramo li dio GMK iz prethodnog primjera na krivulje konstantnog stupnja prigušenja ζ i frekvencije neprigušenih oscilacija ω_n dobiti ćemo sliku 4.5.6. Korak pojačanja između markera je oko 0.1.

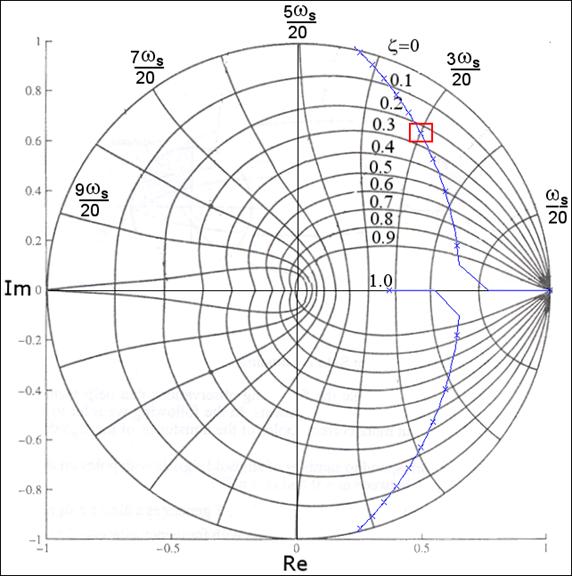
Slika 4.5.6. GMK iz prethodnog primjera superponiran na krivulje konstantnog stupnja prigušenja ζ i frekvencije neprigušenih oscilacija ω_n unutar jedinične kružnice

Za zaokruženi pol pojačanje K je otprilike 1.1, stupanj prigušenja ζ oko 0.25 i frekvencija neprigušenih oscilacija ω_n= 3ω_S/20 = 3π/10 = 0.942rad/s iz čega slijedi da je frekvencija prigušenih oscilacija ω_p= ω_n(1 - ζ²)^1/2=0.912 rad/s i period prigušenih oscilacija T_s oko 6.9 sekundi. Da je to tako pokazuje i VisSim simulacija odziva prikazana na slici 4.5.7.

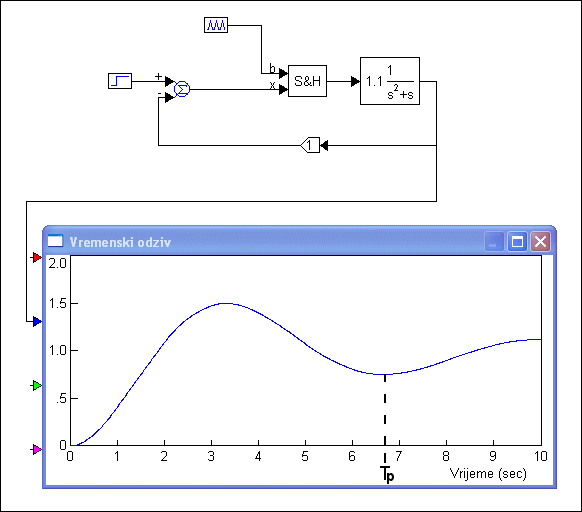
Slika 4.5.7. GMK iz prethodnog primjera superponiran na krivulje konstantnog stupnja prigušenja ζ i frekvencijom neprigušenih oscilacija ω_n unutar jedinične kružnice

GMK je dosta značajan kod projektiranja diskretnih regulatora pa ćemo mu se još vratiti u poglavlju 5, a u nastavku ćemo razmatrati analizu osjetljivosti diskretnih sustava.