Digitalno vođenje on-line (FESB, Split)

2. KONTINUIRANI I DISKRETNI SIGNALI I SUSTAVI

Sve što se događa oko nas, ovisno je o vremenu, u funkciji je vremena. To se odnosi i na sve signale sustava vođenja, bez obzira da li se radi o ulaznim ili izlaznim signalima. U ovom poglavlju obrađuje se razlika između vremenski promjenjivih signala koje nazivamo kontinuirani signali i vremenski promjenjivih signala koje nazivamo diskretni signali. U digitalnim sustavima vođenja bar jedan od signala mora biti diskretan, pa je za digitalne sustave vođenja pojam diskretizacije po vremenu posebno važan.

Klasična automatska regulacija analizira i projektira sustave kod kojih su svi signali kontinuirani, što znači da su definirani, da postoje, da su poznati u svim trenucima vremena. Svi se takvi signali mogu prikazati funkcijskom ovisnošću o vremenu t. Na primjer kod spremnika iz poglavlja 1.3 ulazni tok, izlazni tok i razina funkcije su vremena: q_u = q_u(t), q_i= q_i(t), h = h(t). Regulator prima kontinuirane signale, koji mogu zbog prijenosnih karakteristika osjetila biti dinamički izmijenjeni (zakašnjeli, oslabljeni, pojačani), ali i dalje ostaju kontinuirani. Kod spremnika razina je kontinuirano promjenjiva veličina. Otporničko osjetilo razine pretvara informaciju o razini u električni signal koji i dalje ostaje kontinuiran. Takve signale uobičajeno je nazivati analogni signali. Električni signal na izlazu osjetila razine električna je analogija stvarne razine vode u spremniku.

Pretpostavimo sada da smo za sustav na slici 1.3.3 u prijenosnu liniju od otporničkog osjetila do zbrajala stavili sklopku koja se otvara i zatvara u pravilnim razmacima. Primjer takve sklopke može biti sinkroni motor koji preko reduktora okreće nepravilni valjak.

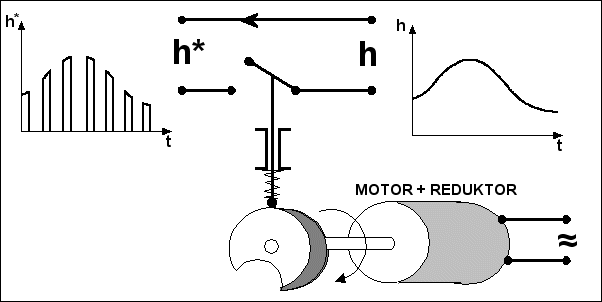
Slika 2.1. Prelazak iz kontinuiranog u diskretni signal

Opruga osigurava da kotva sklopke prati oblik valjka. Kad je kotva na ispupčenom dijelu sklopka je otvorena. Zatvara se samo u maloj udubini. Samo u tom trenutku zbrajalo, a iza njega i regulator prima informaciju o razini vode u spremniku. Uz odgovarajući odabir motora i reduktora to na primjer može biti 100 puta u sekundi. Izlazni signal sustava - razina h, više nije kontinuirana funkcija vremena. Kažemo da smo je kvantizirali po vremenu, da smo je diskretizirali. Signal razine je postao diskretni signal. Grafički to možemo prikazati slikom 2.2. Ukoliko se kontinuirani signal propusti kroz napravu koja provodi diskterizaciju on se pretvara u diskretni signal. Kako bi naglasili razliku diskretni će se signal označavati zvjezdicom. Na primjeru razine kontinuirana vrijednost signala razine označava se h, a diskretna vrijednost h*. T je period kvantizacije ili period uzorkovanja, a je duljina trajanja uzorka.

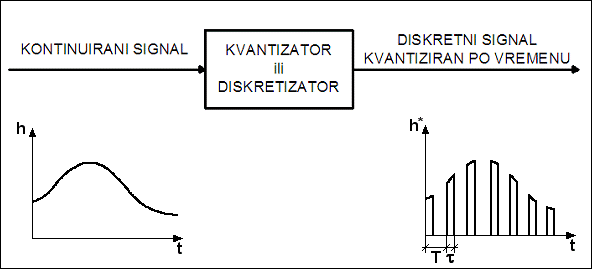
Slika 2.2. Kontinuirani signal i diskretni signal

Svaki kontinuirani signal opisuje se s dvije veličine - vremenom t i funkcijskom vrijednošću (amplitudom) y(t). Zbog toga osim kvantizacije po vremenu može se provesti i kvantizacija po amplitudi, a postoji i treća mogućnost: istovremena kvantizacija i po vremenu i po amplitudi. Slika 2.3 prikazuje sve tri situacije u slučaju kada je period uzorkovanja puno dulji od trajanja uzorka, pa se trajanje može zanemariti. U praksi je upravo to najčešći slučaj.

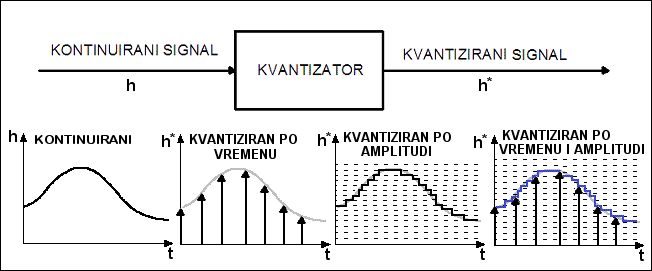
Slika 2.3. Nekvantizirani i kvantizirani signali

Pogledajmo kako se sva tri tipa kvantizacije mogu matematički opisati u duhu teorije sustava.