3. MODELIRANJE DISKRETNIH SUSTAVA

Svijet u kojem živimo je kontinuiran i ovisan o kontinuiranoj varijabli – vremenu t. Dinamičko ponašanje sustava u tom kontinuiranom svijetu opisuje se diferencijalnim jednadžbama. Ovisno o tome da li sustav pokazuje linearno ili nelinearno ponašanje te da li mu se koeficijenti mijenjaju tijekom vremena, opisujemo ga linearnim ili nelinearnim diferencijalnim jednadžbama, diferencijalnim jednadžbama s konstantnim ili promjenjivim koeficijentima itd. Što je jednadžba kompleksnija, to je i teže rješiva, pa se nastoji, kada je god to moguće, pa makar samo i u okolini radne točke, ponašanje složenog sustava prikazati, aproksimirati ekvivalentnim linearnim sustavom. Njegov matematički opis je linearna, diferencijalna jednadžbama s konstantnim koeficijentima. Veći dio kontinuirane regulacije temelji se na ovakvoj aproksimaciji.

Slična je situacija i kod diskretnih sustava s tim da se oni nastoje opisati linearnim jednadžbama diferencija s konstantnim koeficijentima. Iz jednadžbi diferencija jednostavno se izvede i tzv. impulsna prijenosna funkcija na kojoj se temelji "klasični" pristup analizi i sintezi diskretnih sustava ili jednadžbe stanja diskretnih sustava na kojima se temelje neke "modernije" metode.

Uzmimo za primjer sustav integracijskog ponašanja vođen proporcionalnim regulatorom prikazan na slici 3.1. Tipičan primjer je spremnik bez ispusta. Uz zanemarenje nelinearnosti ventila i ograničene visine spremnika (maksimalne vrijednosti koju razina može doseći prije preljevanja) možemo ga opisati sustavom jednadžbi:

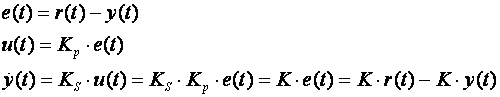
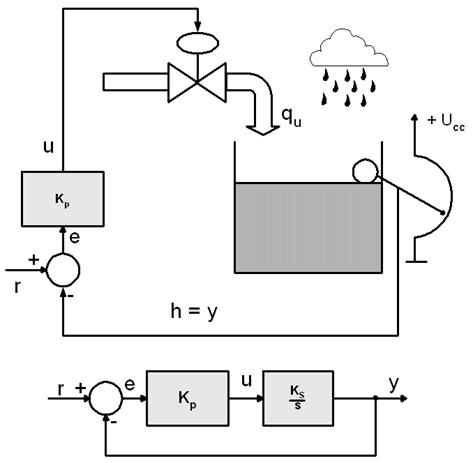
Slika 3.1. Integracijski sustav vođen proporcionalnim regulatorom

Iz ovih jednadžbi slijedi linearna diferencijalna jednadžba prvog reda koja matematički opisuje ponašanje ovog kontinuiranog regulacijskog sustava:

(3.1)

Rješenje jednadžbe predstavlja vremensku ovisnost promjene izlazne varijable (razine u spremniku) u ovisnosti o početnoj razini (početni uvjet) y(0) i vremenskoj promjeni ulazne, referentne veličine r(t) :

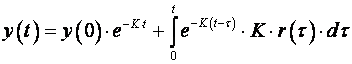(3.2)

Za nulte početne uvjete (prazan spremnik) i skokovitu jediničnu promjenu referentne vrijednost (skokovita pobuda) rješenje jednadžbe (3.2) je:

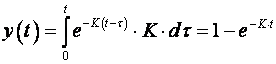(3.3)

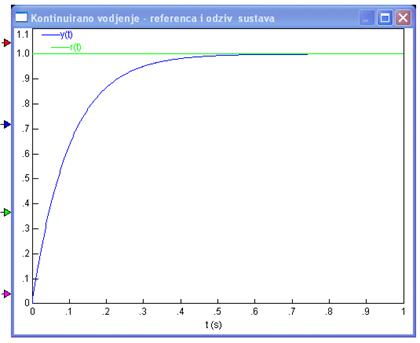
Prikazuje ga slika 3.2 za K_p=10, K_s=1, odnosno K = K_p K_s =10.

Slika 3.2. Odziv regulacijskog sustava sa slike 3.1 na skokovitu pobudu

Zamijenimo li kontinuirani regulator diskretnim i ostavimo K_s = 1, biti će K=K_p (slika 3.3).

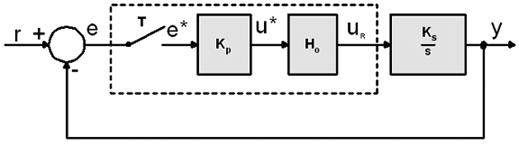
Slika 3.3. Integracijski sustav vođen diskretnim proporcionalnim regulatorom

Slika 3.4. prikazuje sve signale za skokovitu pobudu reference i period uzorkovanja T=0.02.

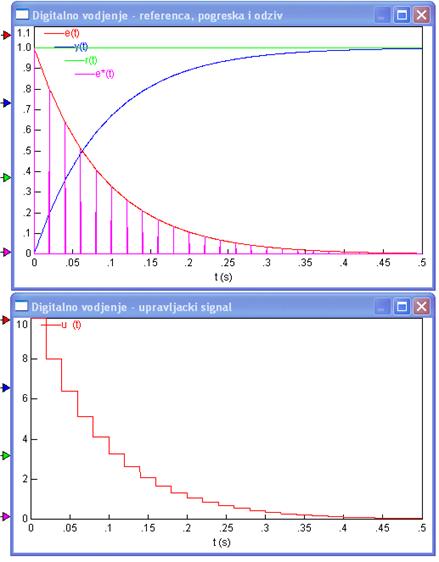
Slika 3.4. Signali integracijskog sustava sa slike 3.3 vođenog diskretnim proporcionalnim regulatorom za T=0.02

Zanimljivo je pogledati što se događa između trenutaka kT i (k+1)T. Situaciju povećano prikazuje slika 3.5.

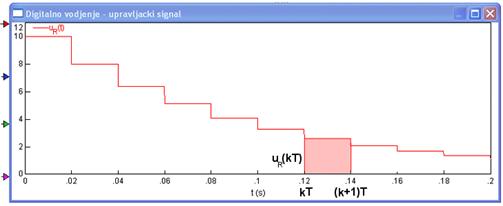
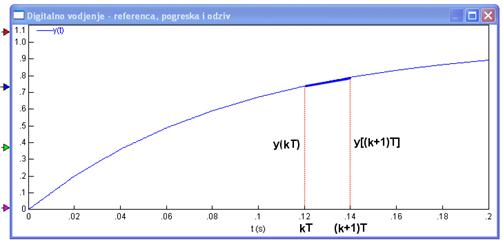
Slika 3.5. Povećani upravljački signal i odziv sustava vođenog diskretnim proporcionalnim regulatorom

Vođeni je sustav čisti integrator pa vrijedi :

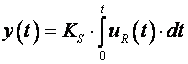(3.4)

U trenutku t=(k+1)T vrijednost integrala y[(k+1)T] bit će jednaka vrijednosti integrala u prethodnom trenutku y(kT) plus površina pravokutnika čije su stranice u_R(kT) i period uzorkovanja T:

(3.5)

Kako je

i ako produkt konstanti označimo sa K = K_P K_S vrijedi:

(3.6)

Nakon sređivanja i dijeljenja s periodom uzorkovanja T dobijemo:

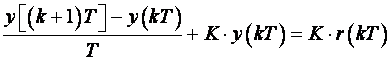(3.7)

Usporedimo li jednadžbu (3.7) i (3.1) uočit ćemo dosta sličnosti. Razlika je što se umjesto vremena t javljaju diskretni vremenski trenuci kT, te umjesto prve derivacije oblik koji nazivamo prva diferencija ili još točnije prva unaprijedna diferencija. Cijela se jednadžba (3.7) zbog toga naziva linearna jednadžba diferencija prvoga reda.

Prva unaprijedna diferencija kraće se piše:

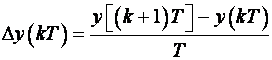(3.8)

pa jednadžba (3.7) izgleda:

(3.9)

i opisuje ponašanje diskretnog regulacijskog sustava sa slike 3.3.

Rezultat možemo poopćiti i zaključiti: Dinamičko ponašanje kontinuiranih sustava opisuje se diferencijalnim jednadžbama, a diskretnih sustava jednadžbama diferencija. Više o jednadžbama diferencija naučiti ćemo u sljedećem poglavlju.