3.1. Matematički opis diskretnog sustava jednadžbama diferencija
Prvu unaprijednu diferencija definirali smo razlikom diskretnih signala u trenucima (k+1)T i kT podijeljenoj s periodom uzorkovanja T. Slično tome druga unaprijedna diferencija koja se označava sa Δ2 y(kT) definira se razlikom prvih diferencija podijeljenih periodom uzorkovanja T:
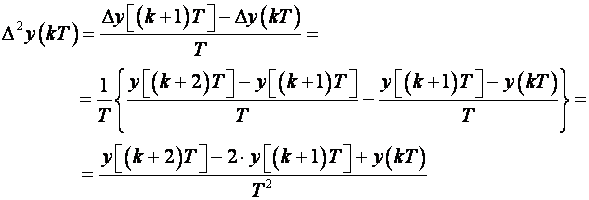(3.1.1)
Treća unaprijedna diferencija Δ3 y(kT) definira se razlikom drugih diferencija itd.
Općenito Δk nazivamo operator k-te diferencije. Operator Δ je linearni operator pa za bilo koje dvije konstante λ i μ vrijedi:
(3.1.3)
Uvedimo sada
još jedan operator – operator pomaka
:
(3.1.4)
gdje je n
cijeli broj, a h realni broj koji može poprimiti bilo koju vrijednosti od 0
do 1 
. Ograničiti ćemo se za sada na cjelobrojne pomake, što
znači da pretpostavljamo da je h =1. U tom ga slučaju niti ne pišemo:
(3.1.5)
Za n = 0 operator pomaka se naziva operator identiteta i označava sa I:
(3.1.6)
Vratimo se sada prvoj diferenciji:
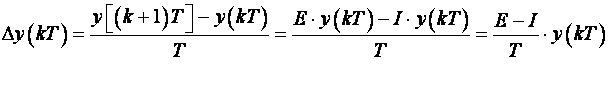(3.1.7)
Očito je da operator prve diferencije možemo pisati:
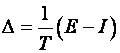(3.1.8)
Na sličan način zapisujemo i operator druge
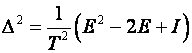(3.1.9)
ili općenito n-te diferencije:
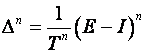(3.1.10)
Zanimljiv je i izraz za proračun n-tog pomaka uz poznate diferencije:
(3.1.11)
Operator pomaka može biti i negativan. Tada se naziva operator zadrške ili operator kašnjenja (eng. Delay Operator):
(3.1.12)
Nedostatak
unaprijedne diferencije je taj što za proračun diferencije u trenutku kT
treba poznavati vrijednosti signala u budućnosti. Upravo zbog toga u
diferencijalnom računu uvedena je i povratna diferencija koja se označava
operatorom 
:
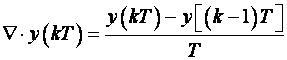(3.1.13)
Druga povratna diferencija je:
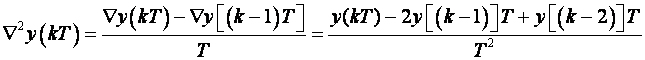(3.1.14)
itd. Operator povratne diferencije također možemo prikazati operatorom identiteta i operatorom pomaka
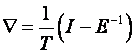(3.1.15)
Unaprijedna i prethodna diferencija vezane su sljedećim izrazima:
(3.1.16)
(3.1.17)
Ponekad se
definira i centralna diferencija
izrazima:
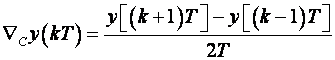(3.1.18)
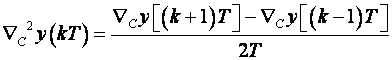(3.1.19)
ali se ona obično u praksi ne koristi, pa se njom dalje nećemo niti baviti.