A-2 Specifikacija odziva u vremenskom području i s-ravnini
Kod definiranja željenog ponašanja sustava obično najprije definiramo par konjugirano-kompleksnih polova koji bi trebali određivati svojstva sustava. Nazivamo ih dominantni polovi. Oni su u s-ravnini najbliže imaginarnoj osi. Ukoliko sustav treba imati više od dva pola ostale polove nastojimo udaljiti što više prema negativnom dijelu realne osi s-ravnine, kako bi njihov utjecaj na ponašanje sustava bio što manji. Dominantni su polovi oni koji u najvećoj mjeri definiraju svojstva sustava, pa željeni vremenski odziv sustava (specifikacije odziva u vremenskoj domeni) definiramo za odziv sustava drugog reda s konjugirano-kompleksnim polovima. Pri tome se obično izabire da pojačanje sustava za istosmjerni signal (ω=0) bude jednako jedinici, što znači da statička prijenosna funkcija sustava treba biti
Odziv takvog sustava na jedinični skok nazivamo oscilatorno prigušeni odziv . Prikazuje ga slika A-2.1.
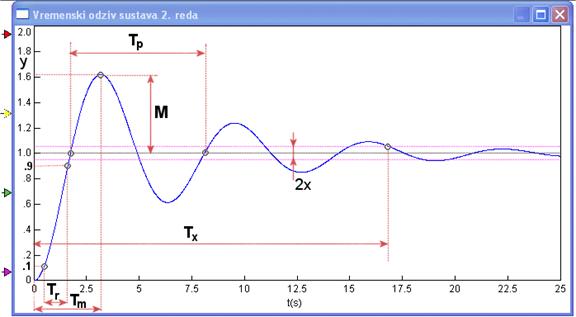
Slika A-2.1. Oscilatorno prigušeni odziv sustava drugog reda
Na slici su označene i neke veličine kojima karakteriziramo vremenski odziv sustava i nazivamo ih specifikacije u vremenskoj domeni:
Tr - vrijeme porasta (eng. RiseTtime )koje se definira kao vrijeme u kojem izlazna veličina zatvorenog regulacijskog sustava naraste sa 10% na 90% svoje vrijednosti ustaljenog stanja ukoliko je na ulazu dovedena jedinična odskočna pobuda. Ponekad se vrijeme porasta definira od 0 do trenutka kada odziv prvi put dođe do vrijednosti ustaljenog stanja, a prije definirano vrijeme se zove vrijeme porasta 10/90 (eng. 10/90 Rise Time)
Tx - vrijeme smirivanja na x % vrijednost (eng. x% Settling Time) koje se definira kao vrijeme za koje odziv sustava uđe u ±x % konačne vrijednosti odziva. Na primjer za situaciju sa slike A-2.1 vrijeme smirivanja na 2% vrijednost je vrijeme za koje odziv sustava uđe u pojas između 0.98 i 1.02 vrijednosti izlaznog signala.
Tp - period prigušenih oscilacija i s njim povezana frekvencija prigušenih oscilacija fp = 1/ Tp i kružna frekvencija prigušenih oscilacija ωP = 2π fp
Tm - vrijeme prvog, maksimalnog prebačaja u odzivu sustava (eng. Peak Time) i
M – iznos prvog, maksimalnog prebačaja (eng. Maximal Overshoot) koji se često definira i u postocima konačne vrijednosti odziva i naziva maksimalni postotni prebačaj (eng. Maximal Percent Overshoot).
Ponekad se definira i Td – vrijeme kašnjenja (eng. Delay Time) kao vrijeme od 0 do trenutka kada odziv dosegne 50 % konačne vrijednosti.
Zanimljivo je ove veličine povezati s položajem polova u s-ravnini sustava drugog reda čiji je to vremenski odziv. Prijenosna funkcija sustava je
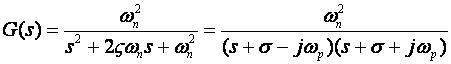(A.2.1)
Slika D-1.2 prikazuje osnovne veličine kojima se karakterizira položaj polova. Prikazan je samo pol u II kvadrantu. Njemu pripada i odgovarajući konjugirano – kompleksni pol u III kvadrantu.
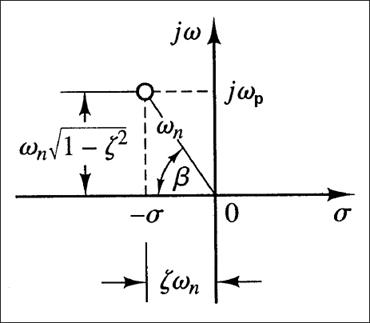
Slika A-2.2. Karakteristične veličine vezane uz položaj konjugirano kompleksnih polova sustava drugog reda
Oznake na slici znače slijedeće:
ωn - kružna frekvencija neprigušenih oscilacija (frekvencija oscilacija sustava na rubu stabilnosti)
ωP - kružna frekvencija prigušenih oscilacija definirana periodom prigušenih oscilacija vremenskog odziva
σ- faktor prigušenja (apsolutna vrijednost realnog dijela položaja pola)
ζ - stupanj prigušenja – veličina između 0 i 1 kojom se definira stupanj prigušenja odziva. Ukoliko je jednak 0, polovi leže na imaginarnoj osi i oscilacije su neprigušene, a ukoliko je jednak 1 polovi leže na realnoj osi i odziv je granično aperiodički pa nema oscilacija.
Lako se pokaže da vrijedi:
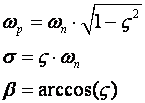(A.2.2)
a iz ovih veličina možemo izračunati i druge specifikacije vremenskog odziva:
M – maksimalni prebačaj
Važno je primijetiti da će prebačaj ovisiti samo o β, odnosno ζ . Prema tome linija maksimalnog prebačaja je linija konstantnog stupnja prigušenja i ona je u s-ravnini polupravac iz ishodišta koji s negativnim dijelom realne osi zatvara kut β (Ovo koristimo u Poglavlju o preslikavanju s-ravnine u z-ravninu).
Slika A-2.3 prikazuje ovisnost maksimalnog prebačaja o stupnju prigušenja za vrijednosti stupnja prigušenja od 0 do 1
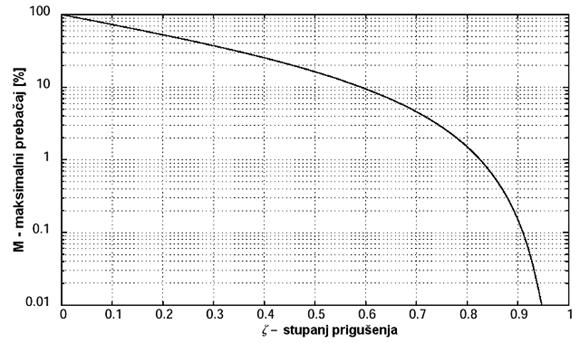
Slika A-2.3. Ovisnost maksimalnog prebačaja o stupnju prigušenja
Tr - vrijeme porasta
Vrijeme porasta od 0 do 100% vrijednosti odziva u ustaljenom stanju računa se izrazom
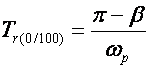(A.2.4)
a vrijeme porasta od 10% do 90% računa se iz nelinearne jednadžbe:
(A.2.5)
Za brzi proračun vrijeme porasta od 10% do 90% obično se koriste aproksimacijske formule nultog, prvog i drugog reda. Aproksimacija nultog reda određuje samo gornju granicu, a aproksimacija drugog reda je bliže stvarnim vrijednostima:
Aproksimacija nultog reda:
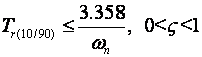(A.2.6)
Aproksimacija prvog reda:
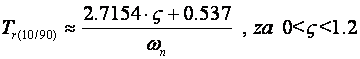(A.2.7)
Aproksimacija drugog reda:
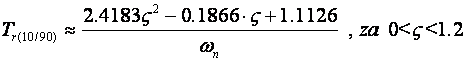(A.2.8)
Slika A-2.4. prikazuje ovisnost normiranog vremena porasta ωn.Tr(10/90) o stupnju prigušenja za različite aproksimacije
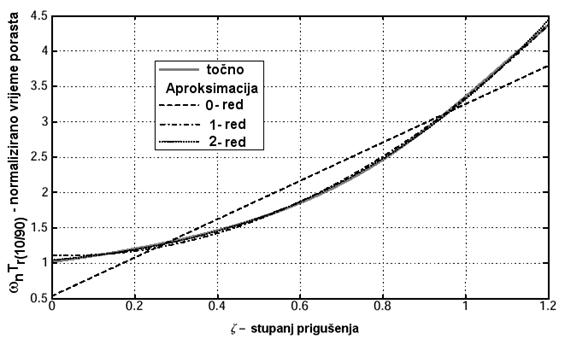
Slika A-2.4. Ovisnost normiranog vremena porasta ωn.Tr(10/90) o stupnju prigušenja za različite aproksimacije
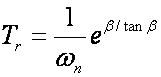(A.2.9)
Tx - vrijeme smirivanja
Vrijeme smirivanja obrnuto proporcionalno ovisi o faktoru prigušenja s koji je po definiciji produkt stupnja prigušenja i neprigušene frekvencije ζ ωn. Stvarni se proračun ponovo temelji na nelinearnoj jednadžbi, a približne vrijednosti se mogu proračunati približnim jednadžbama:
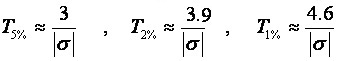(A.2.10)
Slika A-2.5. prikazuje vrijednosti normiranog vremena smirivanja na 5% vrijednost ωn.T5% u ovisnosti o stupnju prigušenja. Na slici su ucrtane i točke aproksimacije.
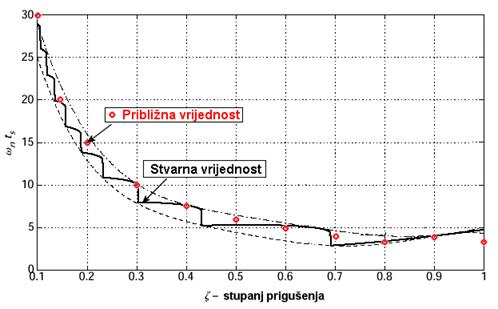
Slika A-2.5. Ovisnost normiranog vremena smirenja ωn.T5% o stupnju prigušenja
Kod diskretnih sustava vrijedi
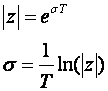
pa se vrijeme smirivanja može računati približnim formulama:
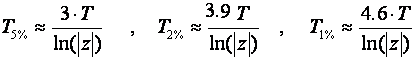(A.2.11)
Tm - vrijeme maksimalnog prebačaja
Ovo je najjednostavnija specifikacija. Vrijeme prvog maksimuma odgovara jednoj polovici periode prigušenih oscilacija
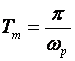(A.2.12)
Posebnu skupinu specifikacija čine integrali pogreške kojima se definira sveukupna kvaliteta odziva sustava. Ima ih više:
Integral pogreške -IE (eng. Integral of Error) - ne koristi se koristi zato što postoji mogućnost da IE bude jednak nuli i u slučaju kad su površine ispod pozitivnog i negativnog dijela signala pogreške podjednake
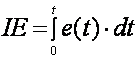(A.2.13)
Integral kvadrata pogreške – ISE (eng. Integral of Square Error) – koristi se kako bi se u obzir uzele i pozitivne i negativne pogreške.
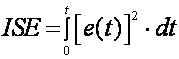(A.2.14)
Integral apsolutne pogreške – IAE (eng. Integral of Absolute Error) – slično kao i u prethodnom slučaju s tim da ga je ovaj integral teže izračunati
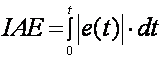(A.2.15)
Ponekad se definira i integral vremenski otežane pogreške tako da se u pod-integralnu funkciju doda i množenje s varijablom t (eng. Weighted Integral Performance Criteria), kako bi se veći značaj dao pogreškama s većim vremenom (bliže stacionarnom stanju). To je pokušaj definiranja mjere koja bi karakterizirala cjelokupni odziv sustava i preferirala sustave s brzim odzivom i što bržim smirivanjem na referentnu vrijednost. Primjeri su
Integral apsolutne vremenski otežane pogreške – ITAE (eng. Integral of Time Avaraging Absolute Error)
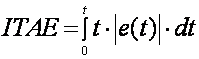(A.2.16)
Integral kvadratne vremenski otežane pogreške – ITSE (eng. Integral of Time Avaraging Square Error) (Napomena: Ponekad se krivo označava i kraticom ISTE koju mi koristimo za integralni kvadrat pogreške otežan kvadratom vremena)
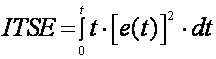(A.2.17)
Integral kvadratne pogreške otežane kvadratom vremenom – ISTE (eng. Integral of Squared Time Avaraging Error)
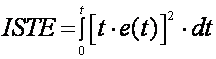(A.2.18)
i općenito sve vremenski otežane kvadratne pogreške mogu se izraziti jednadžbom
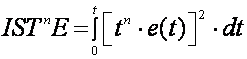(A.2.19)
Za n = 0 dobijemo ISE (A.2.14), a za n = 1 izraz ISTE (A.2.18), dok se ITSE (A.2.17) dobije za n = 1/2.
Kod diskretnih sustava definicije su analogne, s tim što se umjesto integrala može uvesti suma s obzirom da baratamo s diskretnim signalima, na primjer
Suma kvadrata pogreške SSE - (eng. Sum of Square Error)
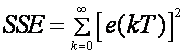(A.2.20)
gdje je e(kT) pogreška u diskretnom trenutku vremena kT.
Sve specifikacije u vremenskoj domeni uzimamo u obzir na način da definiramo dozvoljeno područje unutar kojega se treba naći odziv sustava na jedinični skok. Primjer područja prikazuje Slika A-2.6.
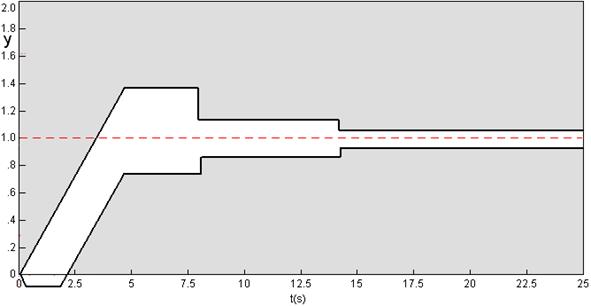
Slika A-2.6. Dozvoljeno područje odziva sustava na skokovitu pobudu
Pogreške ustaljenog stanja vezane su s dijelom odziva u stacionarnom stanju (kada vrijeme t teži u ∞), a vezuju se i sa ulaznom pobudom. Ukoliko je ulazna pobuda jedinični skok pogreška je pogreška ustaljenog stanja pomaka ili položaja (eSSp) , za jediničnu uzlaznu pravčastu pobudu, pogreška je ustaljenog stanja brzine (eSSv), a za jediničnu uzlaznu paraboličnu pobudu pogreška ustaljenog stanja ubrzanja (eSSa). Definiraju se odgovarajućim konstantama pogreški ustaljenog stanja:
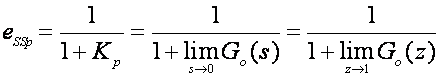(A.2.21)
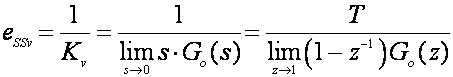(A.2.22)
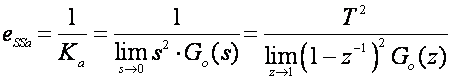(A.2.23)
Konstante pogreški ustaljenog stanja vezane su i sa vremenskim karakteristikama odziva sustava drugog reda (J.R.Leigh, Applied Digital Control, Prentice Hall 1984):
a) Vrijeme za koje odziv dosegne 50% konačne vrijednosti na skokovitu pobudu je približno 1/kv
b) Konstantu pogreške ustaljenog stanja brzine se može i izračunati iz stupnja prigušenja i kružne frekvencije neprigušenih oscilacija
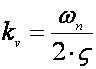(A.2.24)
Koristeći jednadžbu (A.3.4) možemo je vezati i sa pojasom propuštanja sustava ωB. Na primjer za ζ= 1/√2=1/1.41 imamo kv = 0.79 ωB.
Postoje određena ograničenja na ova dva zadnja izraza (vidi literaturu), pa se i ne koriste toliko. Karakteristike odziva se uglavnom određuju nekim od gornjih specifikacija.