Digitalno vođenje on-line (FESB, Split)

4.2.1. Preslikavanje s ravnine u z ravninu

Cilj: Naučiti kako se s ravnina preslikava u z ravninu, i to posebno kako se neki posebni dijelovi s ravnine, na primjer linije maksimalnog prebačaja ili linije konstantne prigušene frekvencije, preslikavaju u z ravninu. Uz ovo poglavlje važno je pročitati i poglavlje Specifikacije odziva u vremenskoj domeni i s području .

Prisjetimo se na početku da je s ravnina ravnina kompleksne frekvencije, a z ravnina ravnina funkcije kompleksne frekvencije.

Kompleksna frekvencija se definira kao s = σ + jω , pa su u s ravnini osi definirane realnim dijelom σ i imaginarnim dijelom jω kompleksne frekvencije. Varijabla z je funkcija kompleksne frekvencije

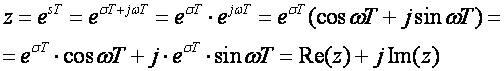(4.2.1)

pa se osi z ravnine označavaju kao Realna os i Imaginarna os.

Jednadžba (4.2.1) u potpunosti definira vezu između s ravnine i z ravnine.

Pogledajmo kako se neke karakteristične točke prebacuju iz s ravnine u z ravninu:

ii)

Zaključak: Negativni dio realne osi s ravnine prebacuje se u realni odsječak između 1 i 0 z ravnine.

iii)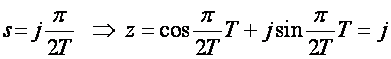

i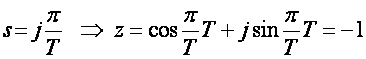v)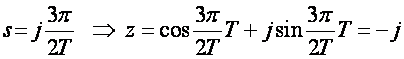

vi)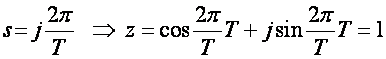

Zaključak: Četiri karakteristične vrijednosti na imaginarnoj osi između 0 i j2π/T preslikavaju se u četiri točke z ravnine koje su na jediničnoj udaljenosti od središta. Lako je pokazati da se bilo koja točka između ovih vrijednosti preslikava na jediničnu kružnicu z ravnine. Ukoliko pređemo na sljedeći odsječak imaginarne osi, između točaka j2π/T i j2^.(2π/T) on će se isto tako preslikavati u jediničnu kružnicu. Isto je i s intervalom između j2^.(2π/T) i j3^.(2π/T) itd. i s intervalima na negativnom dijelu imaginarne osi, pa je konačni zaključak da se imaginarna os s ravnine preslikava u jediničnu kružnicu z ravnine, s tim da je preslikavanje višeznačno s beskonačno točaka s ravnine u jednu točku z ravnine (preslikavanje je surjektivno, ali nije injektivno).

Vratimo li se natrag na jednadžbu (4.2.1) i uvrstimo odgovarajući s dobijemo

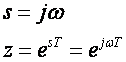
što je jednadžba jedinične kružnice u z ravnini sa središtem u ishodištu. Slika 4.2.1 prikazuje ovu situaciju grafički.

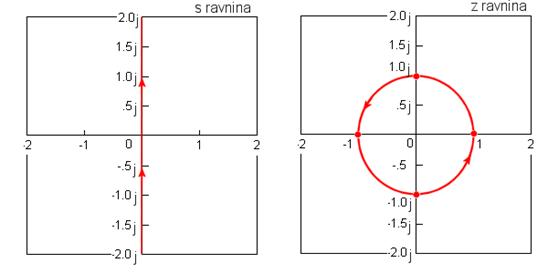
Slika 4.2.1. Preslikavanje imaginarne osi s ravnine u z ravninu

Pomaknemo li se lijevo u s ravnini prema (4.2.1) imamo

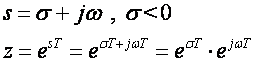
što je u z ravnini također kružnica, ali ovaj put radijusa e^σT (vidi sliku 4.2.2).

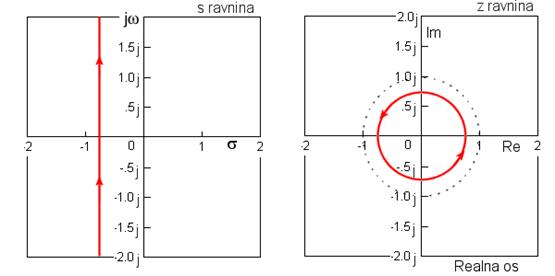
Slika 4.2.2. Preslikavanje pravca paralelnog s imaginarnom osi u z ravninu

Već smo prije spomenuli da se odsječak imaginarne osi između 0 i j2π/T=jω_s preslikava u jediničnu kružnicu. Isto je i s odsječkom imaginarne osi od -jω_s/2 do jω_s/2. Pogledajmo sada detaljno kako se preslikava pojas u s ravnini omeđen odsječkom osi na imaginarnoj osi i polupravcima paralelnim s realnom osi od 0 do ∞ kao što prikazuje slika 4.2.3.

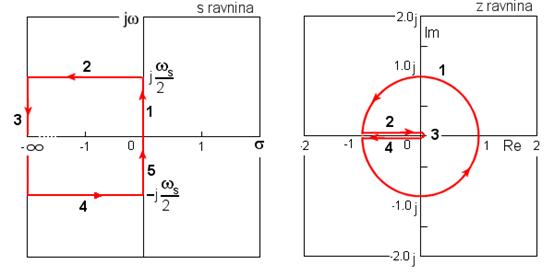
Slika 4.2.3. Preslikavanje pojasa s ravnine u z ravninu

Ovaj pojas s ravnine nazivamo osnovni pojas (eng. Primary Strip). Dio imaginarne osi od 0 do jω_s/2 preslikava se u jediničnu polukružnicu u I i II kvadrantu z ravnine, polupravac paralelan s realnom osi od jω_s/2 do - ∞ u dio realne osi z ravnine od -1 do 0, - ∞ se preslikava u ishodište z ravnine, polupravac paralelan s realnom osi od - ∞ do -jω_s/2 u dio realne osi od 0 do - 1 i na kraju dio imaginarne osi od -jω_s/2 do 0 u jediničnu polukružnicu z ravnine u III i IV kvadrantu. Unutrašnjost osnovnog pojasa preslikava se u unutrašnjost jedinične kružnice.

Na isti se način preslikava i bilo koji drugi jednako široki pojas s ravnine paralelan osnovnom pojasu.

Isti način razmišljanja vrijedi i za pojaseve na desnoj strani s ravnine, s tim da se oni preslikavaju u područje izvan jedinične kružnice z ravnine.

Zanimljivi interaktivni simulator koji povezuje položaj polova sustava 2 reda u s ravnini i z ravnini može se pronači na adresi:

http://controlsystemsacademy.com/0003/0003.html

Simulator je napisan u Matlab-u, a osim položaja polova u s i z ravnini daje i odziv sustava čija prijenosna funkcija, odnosno impulsa prijenosna funkcija ima ta dva pola na pobudu jediničnog skoka. Izgled akrana za primjer konjugirano kompleksne polove prikazuje slika 4.2.3a.

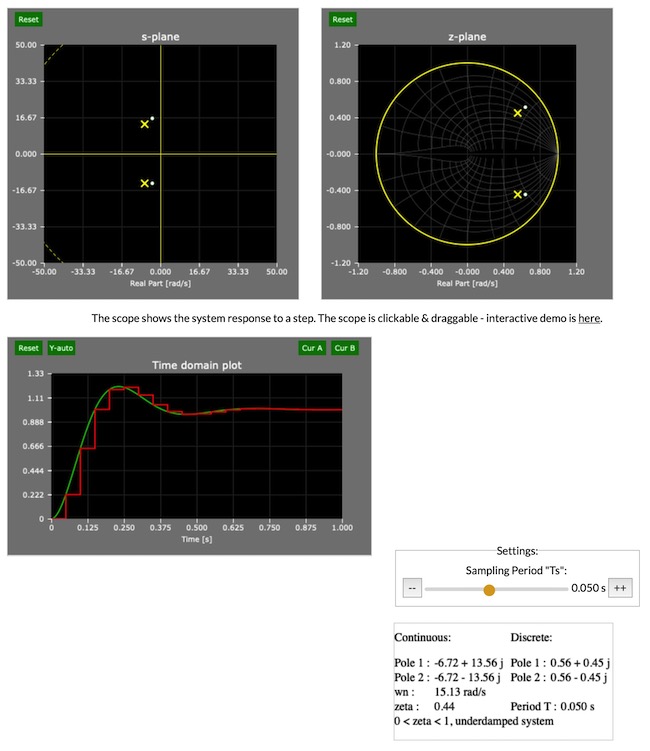
Slika 4.2.3a. Interaktivni simulator veze s i z ravnine za primjer sustava s dva pola (http://controlsystemsacademy.com/0003/0003.html )

Napomena: Prisjetimo se razmatranja o asimptotskoj stabilnosti iz prethodnog poglavlja kada smo kazali da je sustav stabilan ukoliko mu svi polovi leže unutar jedinične kružnice z ravnine. Sada je to pojašnjeno i preko preslikavanja s ravnine u z ravninu. Kontinuirani sustav je stabilan ukoliko mu svi polovi leže na lijevoj strani s ravnine, što u skladu s prethodnim razmatranjem povlači da je diskretni sustav stabilan ukoliko mu svi polovi leže unutar jedinične kružnice z ravnine.

Pogledajmo još kako se neki karakteristični dijelovi s ravnine preslikavaju u z ravninu. Pri tome nas posebno zanimaju oni koji su vezani sa specifikacijama odziva kontinuiranog sustava (vidi Specifikacije odziva u vremenskoj domeni i s području). Posebno nas zanimaju:

a) linije maksimalnog prebačaja (konstantnog stupnja prigušenja ζ),

b) linije konstantne frekvencije prigušenih oscilacija ω_P i

c) linije konstantnog vremena smirivanja na x% vrijednost t_x .

Za definiciju ovih veličina u kontinuiranom području pogledaj poglavlje Specifikacije odziva u vremenskoj domeni i spodručju.

Linija maksimalnog prebačaja je u s ravnini polupravac iz ishodišta koji s negativnim dijelom realne osi zatvara kut β = arc cos(ζ), gdje je ζ stupanj prigušenja. On se kreće od 0 (neprigušeni sustava) do 1 (granično aperiodički sustav). Razlog je taj što jednadžba za proračun maksimalnog prebačaja sustava 2. reda (jednadžba A.2.3. iz Dodatka) ovisi samo o stupnju prigušenja ζ isto kao i kut β. U z ravnini ovaj se polupravac preslikava u spiralu koja počinje u točki 1+j0 i završava u ishodištu. Slika 4.2.4 prikazuje to grafički, a matematički ovo preslikavanje dokazujemo tako da najprije izaberemo točku s=r^.e^j^Φ na polupravcu maksimalnog prebačaja. Sve točke na istom polupravcu će imati isti argument Φ, a amplituda r će se mijenjati od 0 do ∞. Prebacimo se sada u z područje:

Kako smo u II kvadrantu, Φ se kreće od π/2 do π, pa će se cos(Φ) kretati od 0 do -1, a sin(Φ) od 1 do 0. Amplituda |z| odgovarajuće krivulje u z će ravnini počinjati vrijednošću 1 te padati prema 0, dok će joj argument rasti. Rezultat je spirala prikazana na slici 4.2.4.

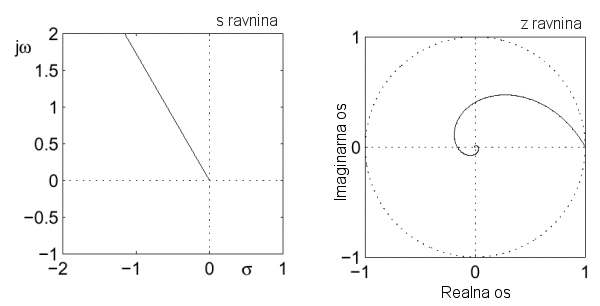
Slika 4.2.4. Preslikavanje pravca maksimalnog prebačaja u z ravninu

Pretpostavimo sada da trebamo projektirati sustav koji ne smije imati maksimalni prebačaj veći od 16%. U skladu s izrazom za proračun maksimalnog prebačaja (vidi Specifikacije odziva u vremenskoj domeni i s području) tolikom prebačaju odgovara kut β=±60⁰ pa oba pola zatvorenog regulacijskog sustava trebaju u s ravnini pasti u područje omeđeno pravcima koji s negativnim dijelom realne osi zatvaraju kut od ±60⁰. U z ravnini tom području odgovara srcolika površina prikazan na slici 4.2.5. Ova se krivulja često u inženjerskom žargonu zove 'srcolika' krivulja.

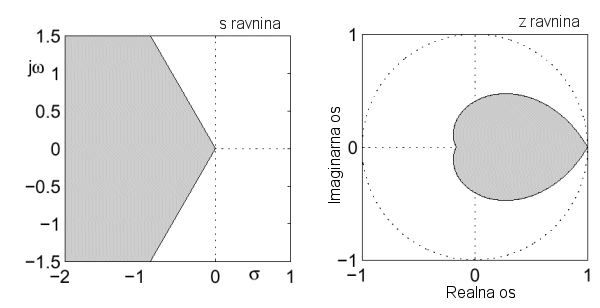
Slika 4.2.5. Preslikavanje područja u kojem je maksimalni prebačaj manji od 16%

Uobičajeno je u z ravnini unutar jedinične kružnice ucrtati krivulje stupnju prigušenja ζ koje odgovaraju krivuljama konstantnog maksimalnog prebačaja. Primjer takvog linija prikazuje slika 4.2.5a. Njima ćemo se često vraćati u dijelu posvećenom sintezi diskretnog regulatora metodom GMK (vidi sliku 4.5.5 na stranici lekcije 4.5 Geometrijsko mjesto korjena diskretnih sustava.

Linija konstantne frekvencije prigušenih oscilacija je u s ravnini horizontalni polupravac paralelan s realnom osi. Ona je ujedno i liniji konstantne periode prigušenih oscilacija zato što je T_P=2π/ω_P , a kako je vrijeme maksimalnog prebačaja polovina periode prigušenih oscilacija, odgovara i liniji konstantnog vremena maksimalnog prebačaja T_m. On se u z ravnini preslikava u radijalne pravce iz ishodišta z ravnine unutar jedinične kružnice. Pogledajte sliku 4.2.3 i segmente 2 i 4 za ω_P=ω_s/2. Za ω_P manji od ω_s/2 raditi će se o radijusima koji s realnom osi zatvaraju kut različit od 0. Na primjer tražimo li područja u s i z ravnini u kojima je prigušena frekvencija manja ili jednaka ω_s/3 u s ravnini to će biti područje unutar osnovnog pojasa, a u z ravnini isječak jedinične kružnice kod kojega je na rubnim područjima argument ±2π/3 (zato što je na primjer za pol u II kvadrantu na 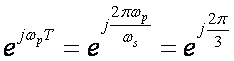. Slika 4.2.6 prikazuje odgovarajuća preslikavanja cijelog područja. Linije konstantne frekvencije prigušenih oscilacija su radijalne, zrakaste linije iz ishodišta z ravnine, a dio imaginarne osi između -ω_s/3 i ω_s/3 preslikava se u dio jedinične kružnice, pa je se sivo područje s ravnine preslikava u dio jedinične kružnice koji se obično u inženjerskom žargonu zove 'siroliko' područje.

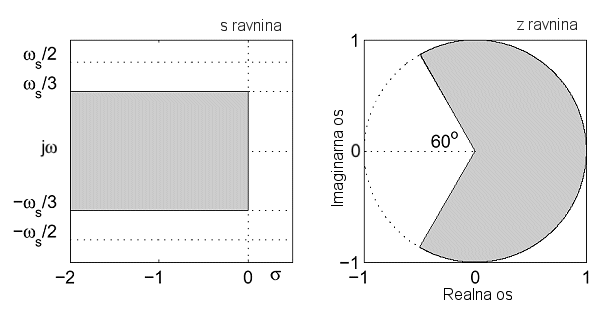
Slika 4.2.6. Preslikavanje dijela s ravnine u kojoj je ω_P≤ω_s/3

Linija konstantnog vremena smirivanja na x% vrijednost je u s ravnini vertikalni pravac paralelan s imaginarnom osi. Već smo ga nacrtali na slici 4.2.2 Sve točke na ovom pravcu imaju isti faktor prigušenja σ, a prema jednadžbi A.2.10. iz Specifikacije odziva u vremenskoj domeni i s području i isto vrijeme smirivanja na x% vrijednost. U z ravnini ovaj pravac se preslikakava u kružnicu unutar jedinične kružnice. Za σ = 0 (vrijeme smirivanja beskonačno), pravac odgovara imaginarnoj osi, pa se preslikava u jediničnu kružnicu, a za σ koji je otišao u - beskonačno (vrijeme smirivanja 0) pravac se svede na točku u ishodištu, što smo već na početku ovog poglavlja i pokazali. Kako i gornjim primjerima, sada se pitamo gdje u z ravnini moraju ležati polovi diskretnog sustava da bi vrijeme smirivanja na x% bilo manje od neke vrijednosti, na primjer vrijeme smirivanja na 2% vrijednost t_2%≤ 2 sekunde (pogledaj primjer ispod). Ova vrijednost određuje neki σ, a on opet neki radjus unutar jedinične kružnice (za prethodne podatke u primjeru ispod smo izračunali da bi taj radijus trebao biti oko 0.37. 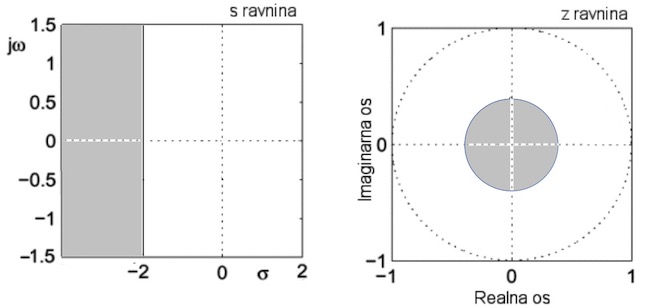U s ravnini područje u kojem je vrijeme smirivanja manje od ovoga je lijevo od pravaca, a u z ravnini unutar te manje kružnice kako zorno pokazuje slika 4.2.6.a.

Slika 4.2.6. Preslikavanje dijela s ravnine u kojoj je t_2%≤ 2 sekunde

Povežimo na kraju ove specifikacije u jednom primjeru:

Primjer

Trebamo projektirati digitalni sustav vođenja tako da odziv zatvorenog regulacijskog sustava (koji je sustav drugog reda) na pobudu jediničnom odskočnom funkcijom zadovoljava sljedeće specifikacije:

a) maksimalni prebačaj M_P≤ 16%

b) vrijeme smirivanja na 2% vrijednost t_2%≤ 3,9 sekunde.

Nacrtajmo prvo specifikacije u s ravnini. Slučaj za ograničeni maksimalni prebačaj smo imali na slici 4.2.5, a za vrijeme smirivanja od 1,95 sekunde imamo

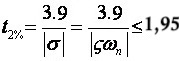
iz čega slijedi |ζ^.ω_P|≥2, što je pravac u s ravnini paralelan s imaginarnom osi. Obje specifikacije zadovoljava zatamnjeno područje na slici 4.2.7.

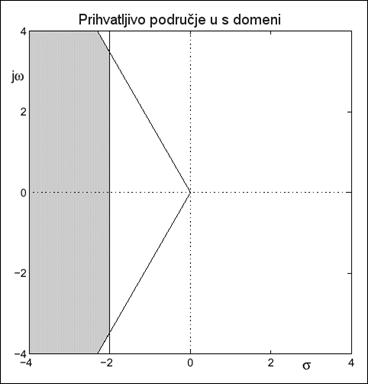
Slika 4.2.7. Specifikacije u s ravnini za sustav drugog reda čiji je prebačaj manji od 16% i vrijeme smirivanja kraće od 2 sekunde

Napomena: ukoliko prijenosna funkcija zatvorenog regulacijskog sustava ima više od dva pola, ili ima nula, onda trebamo paziti da postoje dva pola u zatamnjenom području koje zovemo dominantni polovi, i

a) da su svi ostali polovi ili puno dalje na lijevoj strani s ravnine ili vrlo blizu nulama (poništeni nulama) i

b) sve neponištene nule puno dalje od dominantnih polova.

Vratimo se ponovo na zadatak projektiranja digitalnog sustava vođenja.

Prvo je pitanje izbora frekvencije uzorkovanja. Moramo se osigurati da polovi zatvorenog regulacijskog sustava budu unutar osnovnog pojasa. Pretpostavimo da ih želimo postaviti na sjecište linija β = 60^o i σ=-2. Vrijedi ω_p = 2 tan(60^o)= 2 √3 rad/s ≈ 3.4 rad/s.

Pretpostavimo da želimo imati kružnu frekvenciju uzorkovanja ω_S bar 3 puta veću od kružne frekvencije prigušenih oscilacija ω_p, znači veću od 6√3 rad/s ≈ 10.4 rad/s. Zbog jednostavnijeg računa izaberemo ω_S =4π rad/s, pa je period uzimanja uzoraka T=2π/ω_S = 2π/4π = 0.5 sekundi.

Da bi polovi u z ravnini zadovoljili specifikacije s ravnine trebaju zadovoljiti sljedeće uvjete:

a) Trebaju biti unutar srcolike površine definirane sa ζ =0.5

b) Trebaju biti unutar kružnice radijusa |z|=e^-2T ≈ 0.37 kako bi se zadovoljio zahtjev |σ| ≥ 2;

c) I treće, argumenti polova trebaju biti manji od ± 2π/3 kako bi frekvencija prigušenih oscilacija bila bar tri puta manja od frekvencije uzorkovanja (vidi sliku 4.2.6).

Konačni je rezultat slika 4.2.8.

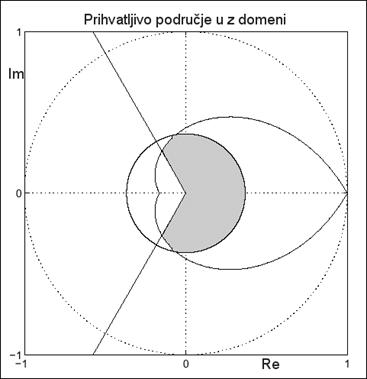
Slika 4.2.8. Specifikacije u z ravnini za sustav drugog reda čiji je prebačaj manji od 16%, vrijeme smirivanja kraće od 2 sekunde i ω_S/ω_p = 3

Napomena: Zahtjev da frekvencija uzimanja uzoraka bude 3 puta veća od frekvencije prigušenih oscilacija nije dovoljan. O tome smo detaljnije govorili u poglavlju 2.2.6. ω_S bi trebao biti najmanje 16 puta veći od ω_p. Ukoliko povećamo frekvenciju uzorkovanja srcolika forma ostaje neizmijenjena, ali se kružnica definirana vremenom smirivanja povećava.

Počinjemo s analizom stabilnosti. Kada je diskretni sustav stabilan doznati ćemo u sljedećem poglavlju.