2.2.6. Izbor frekvencije uzorkovanja
Kod zadataka digitalne obrade signala cilj nam je signal spremiti u digitalnoj formi, izmijeniti ga, te po potrebi vratiti natrag u kontinuirani oblik. Situacija je ovdje relativno jednostavna zato što znamo maksimalnu frekvenciju ulaznog signala pa je primjena teorema uzorkovanja direktna. Na primjer, govorni signal kod kojeg je maksimalna frekvencija 5kHz trebamo uzorkovati frekvencijom 10 kHz ili više.
Kod zadatka digitalnog vođenja izbor frekvencije uzorkovanja temelji se na razumijevanju utjecaja postupka uzorkovanja na ponašanje sustava vođenja. Uobičajeno je da se frekvencija uzorkovanja ne povezuje s najvećom frekvencijom ulaznog signala već s frekvencijskim karakteristikama zatvorenog sustava vođenja ili s vremenskim odzivom izlaznog signala zatvorenog sustava vođenja. Iskustvo kaže da bi frekvencija uzorkovanja trebala biti 10 do 30 puta veća od širine pojasa propuštanja ωB (vidi definicije) zatvorenog regulacijskog sustava.
Vežemo li vrijeme uzorkovanja s vremenskim odzivom zatvorenog regulacijskog sustava vrijedi pravilo da period uzorkovanja T treba biti 4 do 10 puta kraće od vremena porasta Tr (vidi definicije) .
To možda izgleda sporo u odnosu na tipične zadatke obrade signala, ali većina vođenih sustava ponaša se nisko-propusno i vremenske su im konstante veće i čak znatno veće od brzine odziva zatvorenog sustava. Zbog mogućnosti pojave aliasinga važno je koristiti anti-aliasing filter kojem je pojas propuštanja jednak Nyqvistovoj frekvenciji ωN=ωs/2 .
Ilustrirajmo izneseno primjerom sustava drugog reda prijenosne funkcije
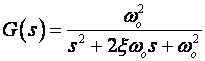 (2.2.27)
(2.2.27)
za ω0= 1.83 i ζ = 0.5 i različite periode uzorkovanja T.
Označimo sa Nr omjer vremena porasta Tr i perioda uzorkovanja T.
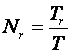 (2.2.28)
(2.2.28)
gdje vrijeme porasta definiramo razlikom vremena u kojima tangenta povučena u točki infleksije siječe pravce y=1 i y=0, a računamo izrazom:
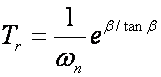 (2.2.29)
(2.2.29)
Napomena: Ovo nije jedini način definiranja vremena porasta. Više detalja o vremenu porasta može se pronaći u Dodatku.
Slika 2.2.20 prikazuje odzive sustava za ζ=0.5, Tr =1 i vrijednosti omjera Nr od 1 do 10.
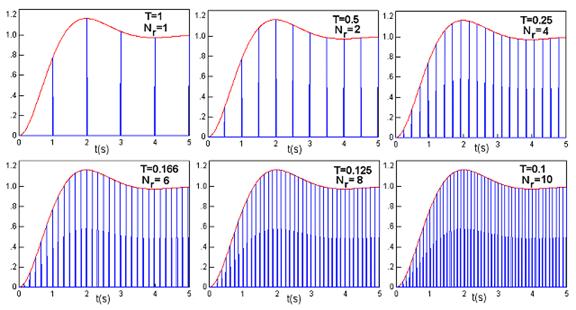
Slika 2.2.20. Odziv sustava 2. reda na jedinični skok za različite periode
uzorkovanja ζ = 0.5 i Tr =1
Prihvatljive su vrijednosti Nr od 4-10.
Kako je jedna od najjednostavnijih specifikacija vrijeme prvog (maksimalnog) prebačaja koja je po definiciji Tm = p/ωp korisno je ovu empirijsku procjenu odabira perioda uzorkovanja prebaciti u odnos vremena prvog maksimalnog prebačaja i perioda uzorkovanja. Uzmimo da je ζ = 0.5 . Iz jednadžbe (2.2.29) i izraza za prigušenu frekvenciju ωp= ωn (1-ζ2)1/2, lako dobijemo da je Tr = 1.584/ωp , pa je omjer Tr / Tm = 0.5 iz čega slijedi da omjer Tm /T treba biti dvostruko veći od omjera Tr / T odnosno vrijeme prvog maksimalnog prebačaja treba biti od 8 do 10 puta duže od perioda uzimanja uzoraka T. Za manji ζ ove bi vrijednosti bile još veće, a za veći ζ manje. Kako je ovo ionako približni proračun možemo se zadovoljiti ovim srednjim zahtjevom da T bude 8 do 20 puta kraći od Tm . Kako Tm odgovara polovini periode prigušenih oscilacija Tp, unutar jedne periode prigušenih oscilacija trebamo imati od 16 do 40 uzoraka. Manje od 16 je nedovoljno, a više od 40 nepotrebno.
Napišimo sva ova pravila o empirijskom izboru perioda uzorkovanja još jedanput pregledno:
Period uzimanja uzoraka određujemo u odnosu na karakteristike vremenskog odziva zatvorenog regulacijskog sustava za kojeg pretpostavljamo da ima par dominantnih konjugirano-kompleksnih polova koji mu u najvećoj mjeri određuju svojstva. Period uzimanja uzoraka T biramo tako da
a) T bude 4 do 10 puta kraći od vremena porasta Tr, odnosno
b) T bude 8 do 20 puta kraći od vremena prvog (maksimalnog) prebačaja Tm, odnosno
c) T bude 16 do 40 puta kraći od periode prigušenih oscilacija Tp.
Ova su pravila posebno važna kod projektiranja diskretnog regulatora postupcima kod kojih željeno ponašanje zatvorenog sustava definiramo željenim položajem para konjugirano-kompleksnih polova, pa ćemo se problemu izbora frekvencije (perioda) uzorkovanja još vraćati u nastavku izlaganja.