Rekonstrukcija ili obnavljanje kontinuiranog signala je inverzna operacija operaciji uzorkovanja. Zadatak je diskretni signal x*(t) rekonstruirati u dijelovima vremena u kojima nije definiran. Rekonstrukcija je kontinuirana funkcija x_R(t). Rekonstrukcija se obavlja u sklopu za obnavljanje koji se još naziva i pritezni sklop, ekstrapolator ili fiksator, a u inženjerskoj praksi koristi se i riječ “holder” prema engleskoj riječi “Hold Circuit”.

Potreba za rekonstrukcijom javlja se  u zadacima digitalne  obrade signala i u zadacima digitalnog vođenja. Kod digitalne obrade signala, digitalni se signal (predstavljen sekvencom binarnih brojeva) treba prebaciti natrag u kontinuirani oblik jednadžbom rekonstrukcije definiranom jednadžbom (2.3.1).

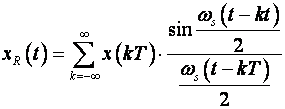                        (2.3.1)

Jednadžba (2.3.1) naziva se Shannonova rekonstrukcija. Nedostatak  joj je što se vrijednost varijable x_R(t) rekonstruira na temelju svih prošlih i svih budućih vrijednosti diskretnog signala x(kT)  (indeks k se mijenja od -∞ do +∞). Shannova rekonstrukcija unosi i kašnjenje te nije pogodna za primjenu u digitalnom vođenju.

U digitalnom se vođenju koriste rekonstrukcije temeljene na razvoju signala u Taylorov red.

Neka nam je poznat signal u trenucima kT i (k+1) T. Zadatak je rekonstruirati signal između ta dva trenutka Taylorovim redom:

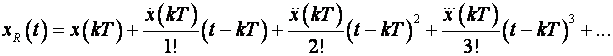                  (2.3.2)

 je prva derivacija signala x(t) u trenutku kT,  druga derivacija itd. Problem je što mi ne poznajemo signal x(t), pa ne možemo znati niti njegovu derivaciju. Poznajemo samo njegove vrijednosti u diskretnim trenucima vremena x(kT) i x[(k+1)T]. Zbog toga derivacije aproksimiramo diferencijama (više o diferencijama u poglavlju 3.1).

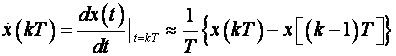                     (2.3.3)

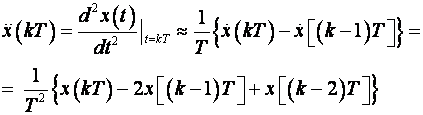                (2.3.4)

itd.

Aproksimacija je dobra ukoliko je period uzorkovanja T dovoljno mali.

Taylorov red (2.3.2) je beskonačan red. Pri rekonstrukciji mi ga ograničavamo na određeni (konačni) broj članova i ovisno o tome sklop za obnavljanje (pritezni sklop) zovemo sklop za obnavljanje  0-tog, 1-tog, 2-tog itd. reda.

U praksi se u najvećem broju slučajeva koristi isključivo sklop za obnavljanje 0-og reda, pa ćemo se u u nastavku baviti samo s njim.