2.3.1. Sklop za obnavljanje (pritezni sklop) 0-tog reda
Engleski se naziva “Zero-order-hold” ili kraće ZOH. Temelji se na rekonstrukciji kontinuirane funkcije samo 0-tim članom Taylorovog reda:
(2.3.5)
što znači da između vremenskih trenutaka kT i (k+1)T rekonstruirani signal zadržava diskretnu vrijednost koju je imao na početku tog intervala (slika 2.3.1).
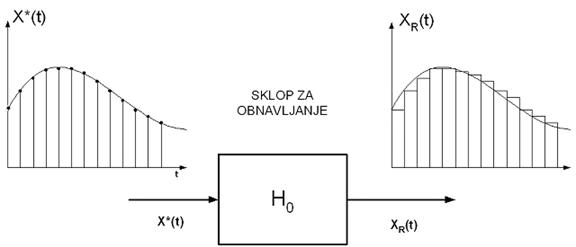
Slika 2.3.1. Obnavljanje funkcije sklopom za obnavljanje 0-og reda
Sklop za obnavljanje unosi pogrešku rekonstrukcije koja se u slučaju neprekinute prve derivacije signala x(t) može procijeniti izrazom:
(2.3.6)
Primjer: Pretpostavimo da je x(t) čisti sinusni signal x(t)= sin ωt. Pogreška koju unosi ZOH u odnosu na vrijednost sinusa od vrha do vrha je:
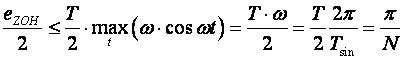
gdje je Tsin perioda sinusa, ω =2p/Tsin, a N broj uzoraka unutar jedne periode N= Tsin/T. Na primjer za 5 uzoraka tijekom periode sinusnog signala pogreška može iznositi 0.6 (60% vrijednosti od vrha do vrha sinusa), za 10 uzoraka 30%, 20 uzoraka 15% itd.
Ponekad se kod izbora perioda uzorkovanja koristi ova procjena pogreške. Na primjer, želimo li da u prije navedenom primjeru pogreška rekonstrukcije bude manja od 1 %, broj uzoraka N unutar jedne periode sinusa Ts treba biti veći od 300.
Sklop za obnavljanje 0-tog reda vrlo je važan element sustava digitalnog vođenja pa je zanimljivo poznavati i njegovu prijenosnu funkciju:
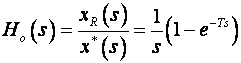(2.3.7)
Kako je izvod jednostavan i zanimljiv navodimo ga u nastavku:
Dokaz:
Uzmimo jedinični impuls i njegovu rekonstrukciju:
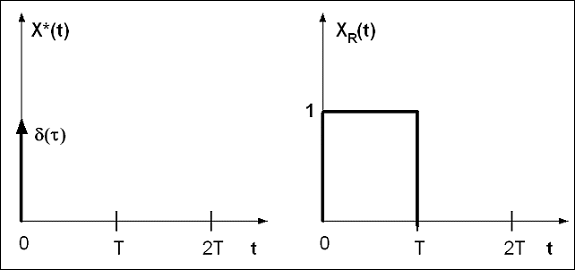
Slika 2.3.2. Jedinični impuls i njegova rekonstrukcija
xR(t) možemo prikazati kao sumu dva skokovita signala: jediničnog skoka u(t) i jediničnog skoka negativne amplitude pomaknutog za period T:
Laplacova transformacija xR(t) je
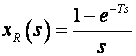
Ulazni signal je Diracova delta pobuda x*(t) = d (t) čija je Laplaceova transformacija x*(t)=1 . Prijenosna funkcija je prema tome:
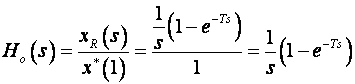
čime je jednadžba (2.3.7) dokazana.
Zanimljivo je pogledati i frekvencijsku karakteristiku sklopa za obnavljanje 0-tog reda.
Napomena:
Naglasimo još jedan put razliku između frekvencijskog spektra i frekvencijske karakteristike. Frekvencijski spektar je vezan sa signalom i predstavlja amplitude i faze članova Fourierovog reda kojim signal prikazujemo, a frekvencijska karakteristika je vezana sa sustavom i kaže što se događa s amplitudom i fazom sinusnog signala nakon njegovog prolaza kroz sustav.
Uvrštavanjem s=jw u jednadžbu (2.3.7) dobijemo
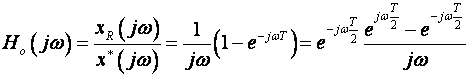
kako je
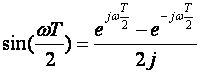
slijedi
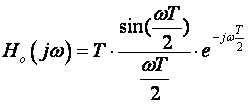
Prvi dio je amplituda, a eksponent e člana argument:
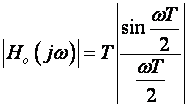(2.3.8)
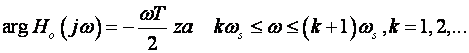(2.3.9)
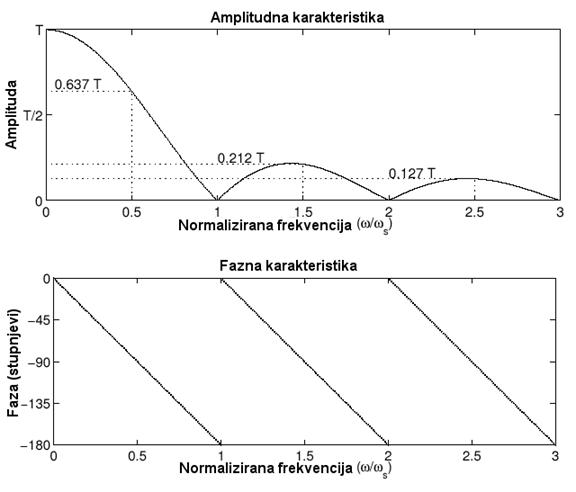
Slika 2.3.3. Frekvencijske karakteristike sklopa za obnavljanje 0-og reda
Svi signali između istosmjernog signala i signala frekvencije ws propušteni kroz pritezni sklop 0-toga reda linearno se fazno zakreću (konstantno kašnjenje u vremenskoj domeni). Kod amplitudne karakteristike prati se zakon (sin x)/x s nul točkama na višekratnicima frekvencije uzorkovanja i vrhovima na frekvencijama 3ws /2 , 5ws /2, ...
Ovdje je zanimljivo spomenuti i to da se jednadžba (2.3.8) vrlo jednostavno modelira u VisSimu. Model i rezultat za T = 1 prikazuje slika 2.3.4.
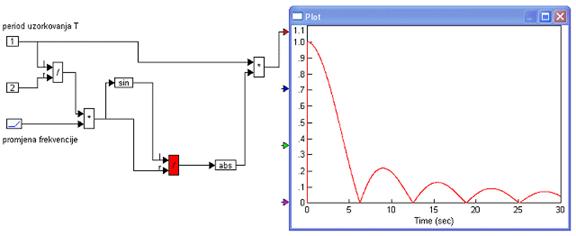
Slika 2.3.4. Modeliranje amplitudne karakteristike sklopa za obnavljanje 0-tog reda u VisSimu (ZOH-amplitudni.vsm)
Sklop za obnavljanje se ponaša kao nisko propusni filter. To je i jasno sjetimo li se diskusije iz poglavlja 2.2.3. Spomenuli smo da je za vraćanje signala iz diskretnog u kontinuirano područje potrebno signal propustiti kroz idealni nisko propusni filter granične frekvencije wN = ws/2. Ucrtali smo ga na sliku 2.3.5 kako bismo naglasili da je sklop za uzorkovanje 0-og reda loš nisko propusni filter. Zato je i rekonstrukcija kontinuirane funkcije sklopom za obnavljanje 0-tog reda gruba i stepeničasta.
Slika 2.3.5. Usporedba karakteristike sklopa za obnavljanje 0-tog reda i idealnog nisko propusnog filtera
Ukoliko želimo bolju rekonstrukciju i bolje filterske karakteristike koristiti ćemo sklopove za obavljanje višeg reda. Njihove frekvencijske karakteristike bliže su idealnom filteru, ali na našu sreću za većinu praktičnih primjena je i ova rekonstrukcija priteznim sklopom 0-tog reda dovoljna.