2.2.3. Ilustracija teorema uzoraka frekvencijskim spektrima uzorkovanog signala
Sve ovo se može lako uočiti ako promotrimo amplitudni frekvencijski spektar (Fourierove koeficijente) signala x(t) i x*(t) = x(t) . δT(t) .
δT(t) periodička funkcija s periodom ωS . Razvijemo li je u Fourierov red dobijemo:
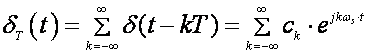 (2.2.11)
(2.2.11)
Lako je pokazati da su Fourierovi koeficijenti:
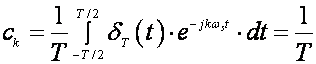 (2.2.12)
(2.2.12)
pa je Fourierov red slijeda impulsa:
 (2.2.13)
(2.2.13)
Kako je x*(t) = x(t) . δT(t) , x*(t) možemo izraziti:
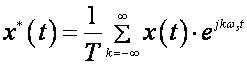 (2.2.14)
(2.2.14)
Primjenom Laplaceove transformacije i teorema prigušenja slijedi:
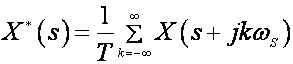 (2.2.15)
(2.2.15)
pa uz zamjenu s = jω dobivamo izraz za frekvencijski spektar uzorkovanog signala:
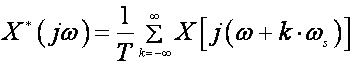 (2.2.16)
(2.2.16)
Ako je frekvencijski spektar osnovnog signala X(jω) ograničen na područje (-ω0,ω0) nakon diskretizacije on će se proširiti po cijeloj frekvencijskoj osi tako da će se osnovni spektar ponavljati oko višekratnika kružne frekvencije uzorkovanja kωS. U ovisnosti o odnosu kružne frekvencije uzorkovanja ωS i maksimalne frekvencije osnovnog signala moguće su dvije situacije koje zorno ilustrira slika 2.2.7. na primjeru amplitudnog frekvencijskog spektra.
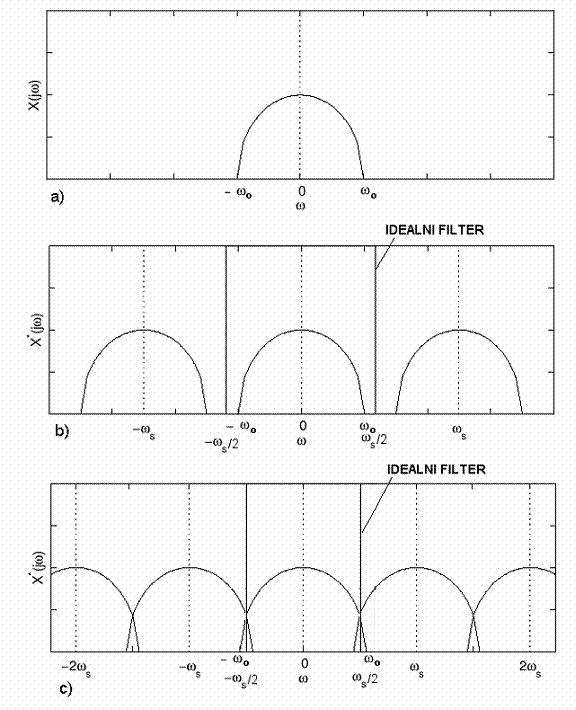
Slika 2.2.7. Amplitudni frekvencijski spektar
a) Signala prije diskretizacije,
b) Signala nakon diskretizacije uz ω0
< (
ωS/2)
c)
Signala nakon diskretizacije uz ω0
> (
ωS/2)
(Zbog jednostavnosti pretpostavili smo da
je fazni frekvencijski spektar jednak nuli – Fourierova transformacija
je realna)
Ukoliko je ω0 < ( ωS/2) (slika 2.2.7b) nema preklapanja pojedinačnih spektara. Uzmemo li idealni filtar koji unutar područja (-ωS/2,ωS/2) ima pojačanje 1 a izvan 0, iz uzorkovanog signala lako izdvajamo (filtriramo) osnovni signal. U slučaju kada je ω0 > ( ωS/2) (slika 2.2.7c) to više nije moguće. Iz uzorkovanog signala nikada više ne možemo vratiti osnovni signal. Nepovratno smo ga izgubili. Ovaj se fenomen naziva frekvencijsko preklapanje ili prema engleskoj riječi aliasing i posebno se razmatra u poglavlju 2.2.5.