4.2.2.  Položaj polova u z ravnini i karakteristični odziv diskretnog sustava

Često korištene metode projektiranja diskretnih sustava temelje se na vezi između vremenskog odziva sustava i položaja polova i nula zatvorenog regulacijskog sustava. U regulaciji temeljenoj na prijenosnoj funkciji (klasična regulacija) to je geometrijsko mjesto korijena (GMK), a u regulaciji temeljenoj na opisu sustava jednadžbama varijabli stanja to su metode temeljene na povratnoj vezi varijabli stanja. Zbog toga je nužno detaljnije proučiti kako položaj polova utječe na vremenski odziv sustava.

U prethodnom poglavlju načelno smo govorili kako se pojedini dijelovi s ravnine prebacuju u z ravninu. Pogledajmo sada kako se polovi na pojedinim lokacijama s ravnine prebacuju u z ravninu i kako to utječe na karakteristični odziv sustava (sustav pobuđen impulsnom Diracovom delta pobudom) koji ovisi samo o polovima sustava.

Napomena: U prethodnom smo poglavlju spominjali slobodni odziv kao odziv sustava na početne uvjete, bez prisustva vanjske pobude, a ovdje spominjemo karakteristični odziv kao odziv sustava na Diracovu delta pobudu. Na prvi pogled ova dva odziva su u kontradikciji, prvi je bez pobude, a drugi uz prisutnu pobudu, međutim između njih postoji povezanost na način da oba odziva ovise samo o polovima sustava. Diracova delta pobuda je definirana samo u nuli, pa možemo smatrati da ona samo postavi početne uvjete (akumulira određenu energiju u dijelovima sustava koji imaju sposobnost akumulacije energije), pa je odziv nakon toga rezultat samo te energije koja se u trenutku 0 akumulirala u sustavu. Upravo zbog toga, kako su zaključci isti, u nastavku umjesto analize pravog slobodnog odziva analiziramo karakteristične odzive.

Krenimo sa slikom 4.2.9 koja prikazuje vezu polova s i z ravnine. U skladu s prethodnim razmatranjem jasno nam je da se polovi na lijevoj strani s ravnine preslikavaju unutar jedinične kružnice z ravnine, a polovi na desnoj strani s ravnine izvan jedinične kružnice z ravnine.

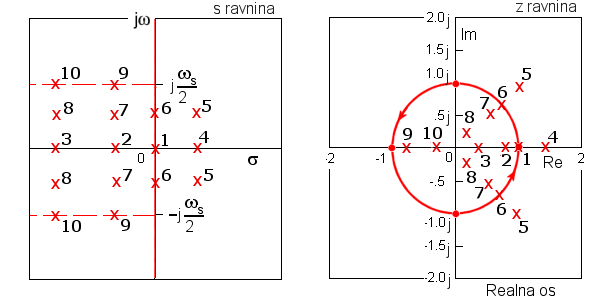
Slika 4.2.9. Preslikavanje polova iz s ravnine u z ravninu

U skladu s Teoremom uzorkovanja svi će polovi biti unutar osnovnog pojasa ili u krajnjem slučaju na granici osnovnog pojasa, što znači da će im imaginarni dio biti manji od ω_S/2. Posebno je zanimljiv položaj polova 7 i 8. Radi se o konjugirano kompleksnim polovima na lijevom dijelu s ravnine, koji kao rezultat daju oscilatorno prigušeni odziv. Oni se u z ravnini preslikavaju isto tako kao konjugirano kompleksni polovi unutar jedinične kružnice u I i IV kvadrantu. Ukoliko je položaj polova u s ravnini određen izrazom

         (4.2.2)

u z ravnini polovi će se izračunati jednadžbom (4.2.1) nalaziti u točkama

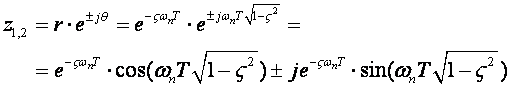         (4.2.3)

Ponekad je zanimljiv i inverzni zadatak. Poznat je položaj polova u z ravnini, a traže se ζ  i ω_n  pomoću kojih možemo odrediti položaje polova u s ravnini (uz pretpostavku da je frekvencija uzorkovanja takva da se polovi nalaze u osnovnom pojasu). Ukoliko su polovi u z ravnini određeni amplitudom r i fazom θ , stupanj prigušenja ζ  i kružnu frekvenciju neprigušenih oscilacija ω_n računamo izrazima

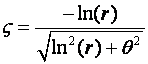         (4.2.4)

i

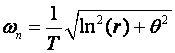         (4.2.5)

a kako vrijedi

         (4.2.6)

možemo pisati i

         (4.2.6)

Na slici 4.2.9 važno je uočiti da je par polova na granici osnovnog pojasa. Konjugirano kompleksni par polova 9 i 10 kojima je imaginarni dio

   (4.2.6)

preslikavaju se u dvostruki pol na negativnom dijelu realne osi z ravnine između 0 i -1. Njegov je položaj određen izrazom

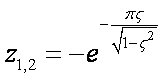           (4.2.7)

Prema tome ukoliko impulsna prijenosna funkcija ima pol na negativnom dijelu realne osi unutar jediničnog kruga to znači da će u odzivu imati komponentu s maksimalnom frekvencijom koju dozvoljava frekvencija uzorkovanja (sjetiti se teorema uzorkovanja - frekvencija prigušenih oscilacija je jednaka polovici frekvencije uzorkovanja). Ovo nam nameće dva zaključka:

a) U sintezi diskretnog regulacijskog sustava metodom podešavanja polova u z ravnini (o kojoj će kasnije biti govora) treba izbjegavati pol na negativnom dijelu realne osi z ravnine, a ukoliko se takav pol ne može izbjeći treba ga postaviti što bliže ishodištu z ravnine. Razlog je taj što će u tom slučaju odgovarajući pol u s ravnini ležati što više lijevo na negativnom dijelu realne osi, pa će mu faktor i stupanj prigušenja biti veći, te će  njegov utjecaj na odziv u vremenskoj domeni kratko trajati.

b) Kod postavljanja zahtjeva na ponašanje regulacijskog sustava preko zadavanja specifikacija na brzinu odziva sustava potrebno je definirati željenu frekvenciju neprigušenih oscilacija ω_n (vidi Specifikacije odziva u vremenskom području i s ravnini) ne smije se zahtijevati veća brzina reagiranja od vrijednosti definirane jednadžbom (4.2.6) što znači da

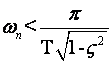   (4.2.8)

Iz svega do sada iznesenog možemo zaključiti da na rezultat preslikavanja iz s ravnine u z ravninu bitno utječe period uzimanja uzoraka T. Pogledajmo to još jedan put pregledno za jedan realni pol i jedan konjugirano kompleksni pol:

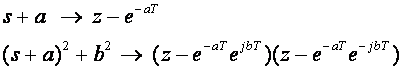   (4.2.9)

Iz ovih izraza možemo primijetiti sljedeće:

a) Aperiodička komponenta kontinuiranog odziva sustava ima pol u točki –a što znači da joj je vremenska konstanta 1/a. Da bi se i nakon diskretizacije sačuvala informacija o početnom sustavu treba biti T<(1/a). Ukoliko je T≪(1/a) preslikani pol u z ravnini će biti pozitivan, manji od jedinice i vrlo blizu točki z=1 (vidi polove 2 i 3 na slici 4.2.9).

b) Kod konjugirano-kompleksnog para polova period uzimanja uzoraka treba biti takav da se tijekom jedne periode osciliranja uzme bar nekoliko uzoraka što znači da T<(1/b). Ako je uz to i T≪(1/a), polovi će se u z ravnini preslikavati blizu točke z=1 zato što im je modul e^-aT.

Zaključak je da previše mali period uzimanja uzoraka koncentrira polove u z ravnini oko točke z = 1 što može imati i negativne efekte na kvalitetu ponašanja dinamičkog sustava.

Na kraju pogledajmo karakteristične odzive (sustav pobuđen impulsnom Diracovom delta pobudom) za različite položaje polova u z ravnini. Kako radimo s linearnim sustavima za koje vrijedi zakon superpozicije iz njih možemo zaključiti koliko će pojedini pol ili par konjugirano kompleksnih polovi pridonositi impulsnom odzivu sustava.

Pogledajmo prvo polove na negativnom dijelu realne z osi. U skladu sa slikom 4.2.9 svi oni u s ravnini moraju imati imaginarni dio jednak polovini kružne frekvencije uzorkovanja. Uzmemo li T = 0.5 kružna frekvencija uzorkovanja će biti ω_S = 2π/0.5 = 4π ≈ 12.57, pa će svi polovi imati imaginarni dio ω_S = 2π ≈ 6.28. Realni dio im je različit a za polove koji izlaze izvan jedinične kružnice prelazi na desnu stranu s ravnine.

Pokažimo i primjer proračuna položaja pola u s ravnini iz poznatog položaja pola u z ravnini. Neka je pol u z ravnini z = - 0.5. Za njega vrijedi r = 0.8 i θ=π , pa imamo:

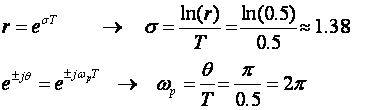
To možemo i provjeriti na duži način i usput izračunati stupanj prigušenja i neprigušenu frekvenciju:

 

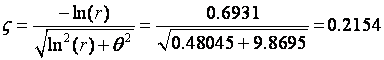
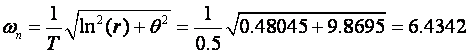
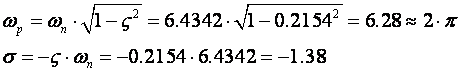
Proračun se podudara s prije spomenutim razmišljanjem o vrijednosti imaginarnog dijela pola u s ravnini.

Sekvencu odziva možemo brzo odrediti na sljedeći način. Uzmimo primjer za pol u točki -0.5. Njemu odgovara impulsna prijenosna funkcija W(z) = 1/(z+0.5). Prebacimo je u oblik s negativnim potencijama varijable z:

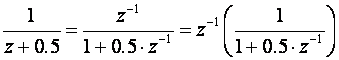
Dio u zagradi je  oblika 1/(1-a) gdje je a = - 0.5 z^-1  . Pišemo ga u tom obliku zato što se  1/(1-a) može lako razviti u red:

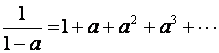
pa u našem slučaju imamo:

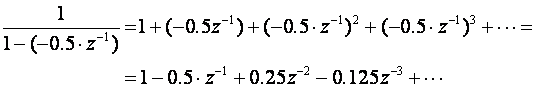
odnosno nakon množenja sa z^-1 dobijemo niz:

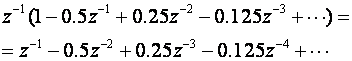
Prisjetimo li se Z - transformacije i vraćanja iz z područja u diskretno područje, negativne potencije varijable z određuju kašnjenje, pa bi u ovom slučaju slijed diskretnih signala karakterističnog odziva dobivenih kao doprinos pola u točki z = - 0.5 bio:

Imamo kašnjenje za jedan diskretni trenutak vremena (rezultat množenja sa z^-1 ) i nakon toga padajuću sekvencu (u ovom slučaju sekvenca pada geometrijskom progresijom). Kašnjenje za jedan diskretni trenutak vremena javlja se onda kada računamo utjecaj pojedinačnog pola na karakteristični odziv. Ukoliko su polovi konjugirano-kompleksni kašnjenje će biti dva diskretna trenutka vremena. Ovo kašnjenje nas ne treba zabrinjavati, ali kako njega u odziv unosi i simulacijski program VisSim na sljedećim je slikama ono zadržano.

Slika 4.2.11. prikazuje odgovarajuće polove u s i z ravnini te karakteristični odziv sustava. Svi su odzivi proračunati u VisSimu, a kako VisSim nema Diracovu impulsnu pobudu, generirali smo je tako da smo oduzeli dvije sekvence slijeda Diracovih impulsnih pobuda, od kojih je ona s negativnim predznakom bila zakašnjena za jedan diskretni trenutak vremena. Slika 4.2.10 prikazuje simulacijski model za pol u točki -0.5. Izlaz iz bloka koji simulira impulsnu prijenosnu funkciju je propušten kroz sklop za obnavljanje, pa smo izlaz još jedan put uzorkovali kako bismo dobili diskretnu sekvencu. Sve sekvence impulsa imaju T = 0.5.

 

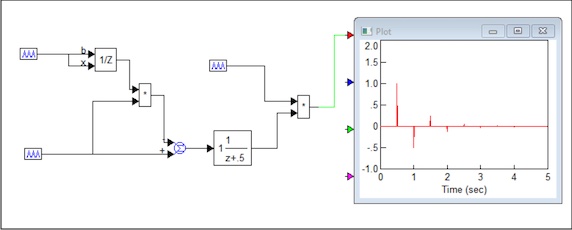
Slika 4.2.10. VisSimov model za proračun karakterističnog odziva (karakteristicni_odziv.vsm)

 

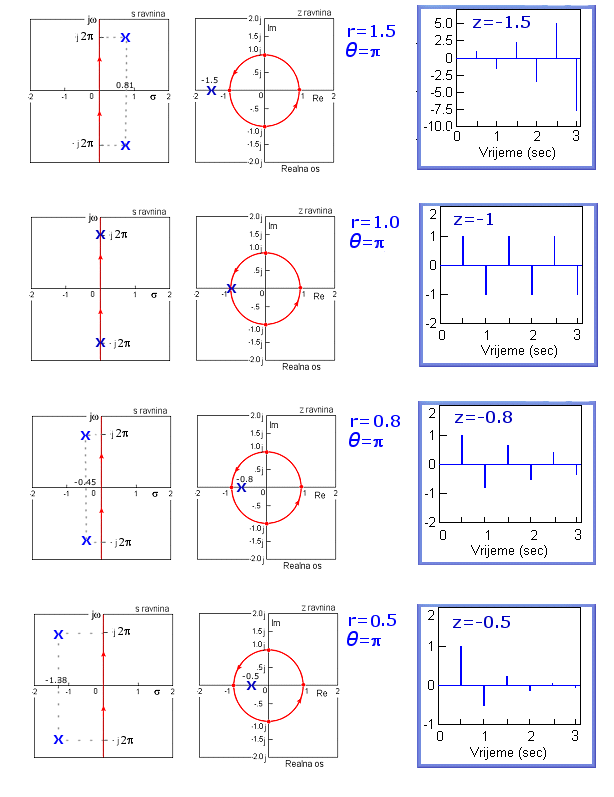
Slika 4.2.11. Položaj polova u z ravnini i karakteristični odziv diskretnog sustava (odziv na impulsnu Diracovu delta pobudu) za T = 0.5 – polovi na negativnoj realnoj osi z ravnine (z_1,2=r^.e^±jθ)

Sljedeću grupu čine polovi na pozitivnom realnom dijelu z osi. U s ravnini njima odgovaraju polovi na realnoj osi (zato što je za njih kut θ  jednak nuli). Za polove unutar jedinične kružnice odziv brže ili sporije teži nuli ovisno o položaju pola. Za pol u točki z=1 imamo stalnu sekvencu (ovaj pol odgovara polu u ishodištu s ravnine koji definira integracijsko ponašanje, a integral Diracove pobude je jedinični skok), a za polove izvan jedinične kružnice imamo rastuću sekvencu.

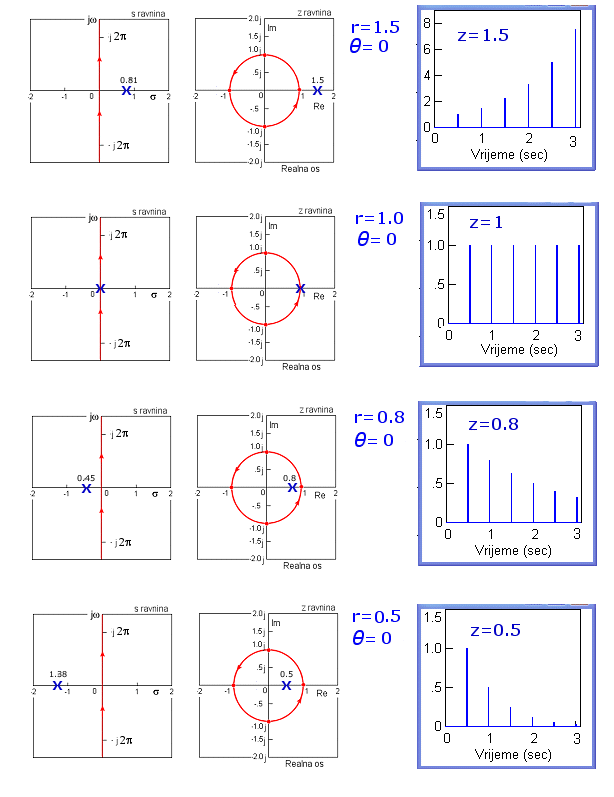
Slika 4.2.12. Položaj polova u z ravnini i karakteristični odziv diskretnog sustava (odziv na impulsnu Diracovu delta pobudu) za T = 0.5 – polovi na pozitivnoj realnoj osi z ravnine (z_1,2=r^.e^±jθ)

Kako nas polovi izvan jedinične kružnice u biti ne zanimaju, za polove unutar jedinične kružnice dobivene rezultate možemo poopćiti. Ukoliko se pol nalazi na pozitivnom dijelu realne osi z ravnine u točki p, karakteristični odziv je padajuća sekvenca sa potencijom vrijednosti pola p^k-1, s tim da je vrijednost u nuli nula zbog prisutnog pomaka za jedan diskretni trenutak: 0, p⁰, p¹, p², ... Ukoliko su polovi na negativnom dijelu realne osi, amplitude diskretnih vrijednosti ostaju iste, ali sekvenca postaje alternirajuća (svaki diskretni trenutak mijenja predznak). 

Analizirajmo sada slučaj konjugirano-kompleksnih polova. Iako imaginarna os u z ravnini nema nikakvo posebno značenje (kao što je imala u s ravnini) zadržimo se zbog jednostavnosti proračuna na polovima koji se nalaze baš na njoj u točkama ±jp. Oba konjugirano kompleksna pola doprinose impulsnoj prijenosnoj funkciji faktorom

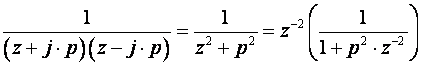
pa je odgovarajuća diskretna sekvenca njihovog doprinos 

Ponovo imamo alternirajuću sekvencu kod koje je svaki drugi član jednak nuli i naravno kašnjenje od 2 diskretna trenutka vremena o kojem smo prije već govorili. Sekvenca je za polove unutar jedinične kružnice prigušena, za polove izvan nje raspirujuća, a na jediničnoj kružnici imamo konstantnu sekvencu. Slika 4.2.13 prikazuje karakteristični odziv za 4 tipična pola.

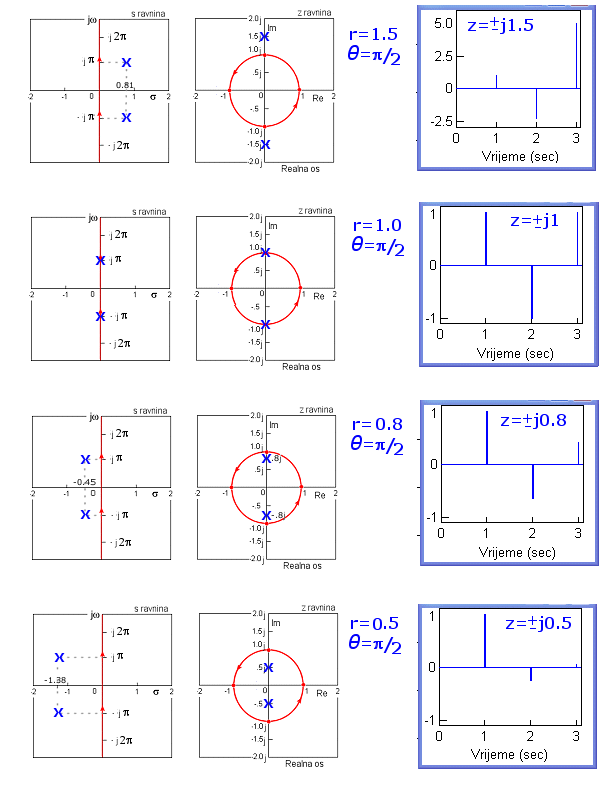
Slika 4.2.13. Položaj polova u z ravnini i karakteristični odziv diskretnog sustava (odziv na impulsnu Diracovu delta pobudu) za T = 0.5 – polovi konjugirano-kompleksni na imaginarnoj osi z ravnine (z_1,2=r^.e^±jθ)

Četvrti slučaj su konjugirano kompleksni polovi z ravnine. Pogledajmo najprije polove u I i IV kvadrantu koji generiraju oscilatorno prigušeni odziv. Na slikama je uneseno i prisutno kašnjenje od dva diskretna trenutka vremena zbog prisustva z^-2 u brojniku.

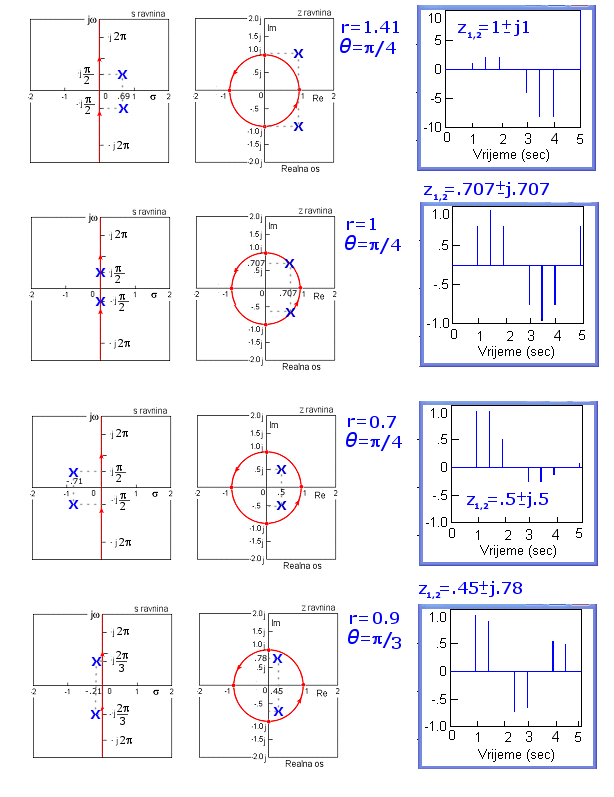
Slika 4.2.14. Položaj polova u z ravnini i karakteristični odziv diskretnog sustava (odziv na impulsnu Diracovu delta pobudu) za T = 0.5 – polovi konjugirano-kompleksni na desnoj strani z ravnine (z_1,2=r^.e^±jθ)

Odziv je sinusoidalan s eksponencijalnom envelopom koja ovisi o modulu r. Što je r veći to je prigušenje slabije. Frekvencija oscilacija je vezana s argumentom pola u z ravnini θ  i vrijedi izraz

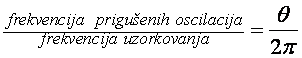      (4.2.10)

Pogledajmo primjer sa slike 4.2.14 U prva tri slučaja θ  je bio , pa je

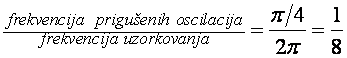
što znači da je frekvencija uzorkovanja 8 puta veća od frekvencije prigušenih oscilacija, odnosno da je perioda uzorkovanja 8 puta kraća od periode prigušenih oscilacija, pa ćemo tijekom jedne periode prigušenih oscilacija imati 8 diskretnih vrijednosti. U zadnjem primjeru θ je bio π/3, pa smo u jednoj periodi prigušenih oscilacija imali 6 diskretnih vrijednosti.

I na kraju konjugirano-kompleksni polovi u II i III kvadrantu čiji karakteristični odziv prikazuje slika 4.2.15. I ovdje imamo kašnjenje od dva diskretna trenutka vremena. U ovom se slučaju radi, slično kao i kod polova na negativnom dijelu realne z osi, o alternirajućoj sekvenci, s tim što je ona fazno pomaknuta, pa se dogodi da je vrijednost pojedinog diskretnog signala jednaka nuli. U prva tri primjera za θ=3π/4 nuli će biti jednak četvrti diskretni signal, a u četvrtom slučaju kada je θ =2π/3 nuli će biti jednak treći diskretni signal

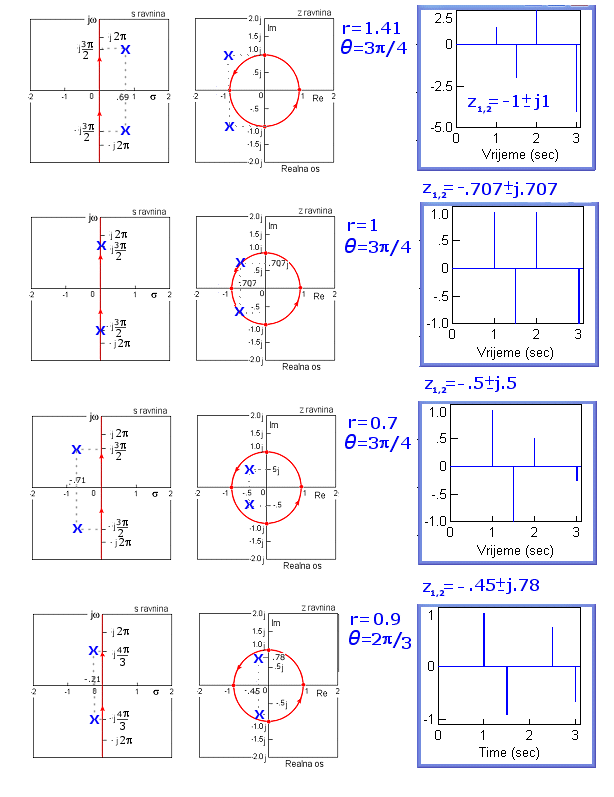
Slika 4.2.15. Položaj polova u z ravnini i karakteristični odziv diskretnog sustava (odziv na impulsnu Diracovu delta pobudu) za T = 0.5 – polovi konjugirano-kompleksni na lijevoj strani z ravnine (z_1,2=r^.e^±jθ)

Iz svega do sada iznesenog bitno je zapamtiti da se dinamički odziv vezan s položajem polova u z ravnini uvijek interpretira u svjetlu frekvencije uzorkovanja. Bez poznavanja frekvencije uzorkovanja ne možemo povezati nikakav realni zaključak s položajem polova u z ravnini.

Posebno važno pitanje je pitanje dominantnih polova. U s ravnini dominantni polovi su bili oni koji su bliže imaginarnoj osi, pa za njih slobodnom (i karakterističnom) odzivu treba duže da dođe do nule. Znajući vezu između s i z ravnine, kod diskretnih sustava zaključak je direktan: Dominantni polovi su oni koji se nalaze bliže jediničnoj kružnici. Pri tome već i male razlike u udaljenosti mogu biti značajne. Pogledajmo primjer.

Zaključak je da već male razlike u poziciji polova odlučuju da li će on biti dominantan ili ne.

U sljedećem poglavlju bavimo se analizom točnosti diskretnog regulacijskog sustava. Pri tome nam je posebno važna točnost u ustaljenom stanju nakon prelaska prelazne pobude, a nju definiraju pogreške ustaljenog stanja.

.: Sljedeća stranica > Točnost i pogreške ustaljenog stanja