Digitalno vođenje on-line (FESB, Split)

4.3. Točnost i pogreške ustaljenog stanja

Cilj: Ukoliko je sustav stabilan, jedno od najčešće spominjanih pitanja je koliko je točan, koliko točno izlaz sustava prati pobudni signal. U ovom poglavlju cilj nam je naučiti kako se točnost mjeri i na koji način možemo odrediti kolika će biti točnost sustava poznavajući pobudu i impulsnu prijenosnu funkciju sustava.

Naglasili smo da se o točnosti sustava može govoriti tek ukoliko je on stabilan. Razlikujemo dinamičku točnost i statičku točnost koju obično nazivamo točnost u ustaljenom stanju ili točnost ustaljenog stanja. Točnost procjenjujemo odstupanjem ostvarenog odziva sustava y(t) i željenog odziva sustava r(t). Za regulacijski sustav sa slike 4.3.1 vrijedi

(4.3.1)

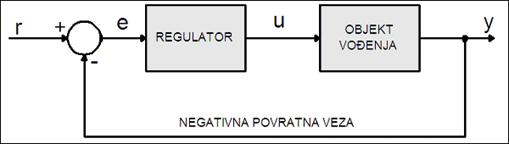
Slika 4.3.1. Jednostavni regulacijski sustav s negativnom povratnom vezom

e(t) je pogreška ovisna o vremenu.

Analiza dinamičke točnosti vezana je s promatranjem dinamičkog mijenjanja pogreške, pa možemo definirati

- maksimalnu pozitivnu dinamičku pogrešku (koja je obično na početku promatranja ukoliko sustav nema početno stanje),

- maksimalnu negativnu pogrešku (koja se obično naziva i maksimalni prebačaj – pogledaj Specifikacije odziva u vremenskom području i s ravnini),

- kumulativnu pogrešku između 0 i nekog vremenskog trenutka t. Ona može biti:

Integral pogreške -IE (eng. Integral of Error)

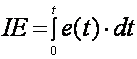(4.3.2)

Integral kvadrata pogreške – ISE (eng. Integral of Square Error) – koristi se kako bi se u obzir uzele i pozitivne i negativne pogreške. Kod integralne pogreške može se dogoditi da je IE jednak 0 zato što su površine ispod pozitivne i negativne pogreške jednake.

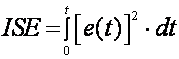(4.3.3)

Integral apsolutne pogreške – IAE (eng. Integral of Absolute Error) – slično kao i u prethodnom slučaju

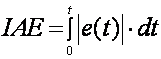(4.3.4)

Ponekad se definira i integral vremenski otežane pogreške tako da se u podintegralnu funkciju doda i množenje s varijablom t, na primjer

Integral apsolutne vremenski otežane pogreške – IATAE (eng. Integral of Absolute Time Averaging Error) – kako bi se veći značaj dao pogreškama s većim vremenom (bliže stacionarnom stanju)

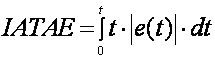(4.3.5)

Kod diskretnih sustava definicije su analogne, s tim što se umjesto integrala može uvesti suma s obzirom da baratamo s diskretnim signalima, na primjer

Suma kvadrata pogreške SSE - (eng. Sum of Square Error)

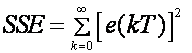(4.3.6)

gdje je

(4.3.7)

Dinamička točnost se uzima u obzir kod definiranja specifikacija na temelju kojih se projektira regulator. Na primjer zada se: projektiraj regulator kome maksimalni prebačaj i njegovo vrijeme neće preći određenu vrijednost. U drugom slučaju nastoji se da integral (suma) kvadratne (ili apsolutne) pogreške bude što manja itd. O svemu tome govoriti ćemo u 5. poglavlju Digitalno vođenje.

Na ovom nas mjestu prije svega zanima statička točnost, razlika između dobivenog i željenog odziva kada sustav dođe u stacionarno ili ustaljeno stanje. Zbog toga se i zovu pogreške stacionarnog ili ustaljenog stanja. Teorijski sustav će u ustaljenom stanju biti tek kada vrijeme bude u beskonačnosti pa matematički pogreške ustaljenog stanja definiramo limesom:

(4.3.8)

U kontinuiranom području proračunavamo ih tako da pređemo u Laplaceovo područje. Za sustav sa slike 4.3.1 možemo pisati:

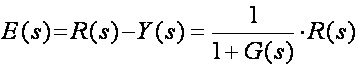(4.3.9)

a po teoremu o konačnoj vrijednosti slijedi:

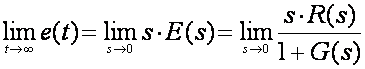(4.3.10)

Vidimo da pogreška ovisi:

- o prijenosnoj funkciji sustava, i

- o pobudnoj funkciji

pa se zbog toga definira nekoliko pogrešaka ustaljenog stanja. Najviše se koriste tri:

- pogreška položaja ili pomaka (eng. Position Error) koja se definira u slučaju kada je pobuda sustava jedinična odskočna funkcija – r(t) = u(t),

- pogreška brzine (eng. Velocityn Error) koja se definira kada je na ulazu sustava jedinična uzlazna pravčasta pobuda – r(t) = t, i

- pogreška ubrzanja (eng. Acceleration Error) koja se definira kada je na ulazu sustava jedinična uzlazna kvadratna pobuda – r(t) = t².

Kolika će pogreška biti ovisi o prijenosnoj funkciji sustava. Jednostavno se može pokazati da su pri tome od presudnog značaja polovi u ishodištu s ravnine. U regulaciji je uobičajeno da polovi u ishodištu definiraju tzv. 'vrst' sustava, pa kažemo da je sustav nulte vrsti ukoliko nema polova u ishodištu, prve vrsti ukoliko ima jedan pol u ishodištu itd. Vrijedi sljedeća tablica

Slika 4.3.2. Vrijednosti pogreški ustaljenog stanja za različiti broj polova u ishodištu

Zanimljivo je pogledati što rezultati iz tablice na slici 4.3.2 znače na odzivu sustava. Slika 4.3.3 prikazuje sve pogreške ustaljenog stanja za sustav 0-vrsti prijenosne funkcije otvorene petlje G(s) = 1/(s+1).

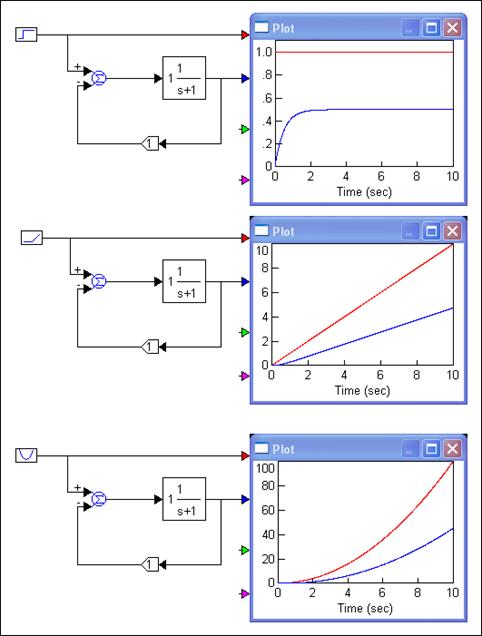
Slika 4.3.3. Pogreške ustaljenog stanja (položaja, brzine i ubrzanja) za sustav nulte vrsti prijenosne funkcije otvorene petlje G(s) = 1/(s+1) (ustaljene_pogreske.vsm)

Gornja krivulja je referentni signal, a donja izlaz regulacijskog sustava. Konstantna pogreška ustaljenog stanja znači da je razmak između referentnog signala i izlaza konstantan, dok beskonačna pogreška znači da se signali udaljavaju kako vrijeme raste. Na primjer za pogrešku brzine, referentni signal i izlaz sustava su divergentni pravci, a za pogrešku ubrzanja divergentne parabole.

Slika 4.3.4 prikazuje pogreške ustaljenog stanja za sustav 1 – vrsti prijenosne funkcije otvorene petlje G(s) = 1/s(s+1).

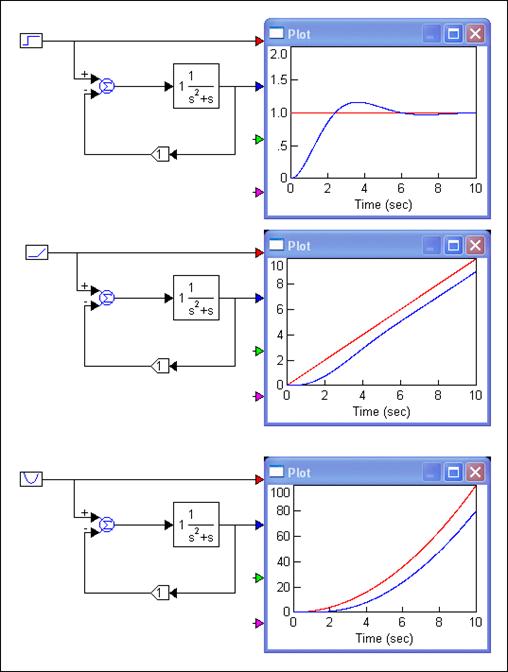
Slika 4.3.4 Pogreške ustaljenog stanja (položaja, brzine i ubrzanja) za sustav prve vrsti prijenosne funkcije otvorene petlje G(s) = 1/s(s+1) (ustaljene_pogreske.vsm)

Konstantna pogreška ustaljenog stanja brzine znači da se nakon prestanka prelazne pojave izlaz sustava ustali na pravcu koji je paralelan referentnom signalu što znači da će izlaz sustava u vrijednosti zadane referentnim signalom doći uz konstantno kašnjenje. Beskonačna pogreška su divergentne parabole reference i izlaza.

I na kraju slika 4.3.5 prikazuje pogreške ustaljenog stanja za sustav 2–vrsti prijenosne funkcije otvorene petlje G(s) =(s+1)²/s²(s+2).

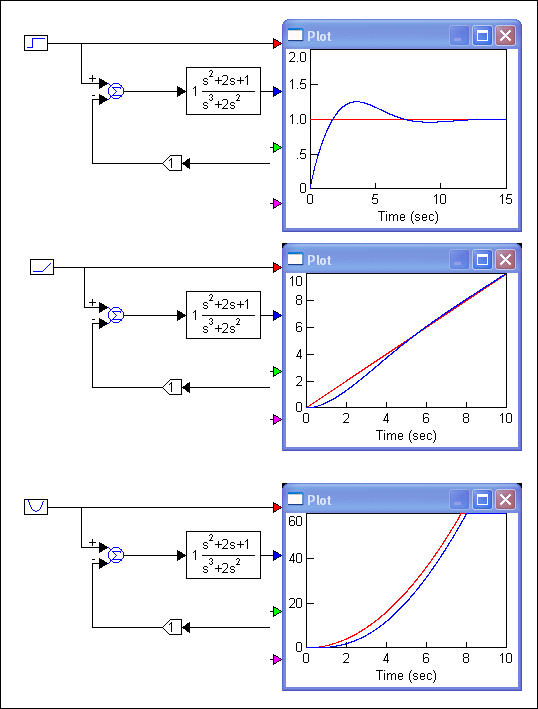
Slika 4.3.5. Pogreška ustaljenog stanja (položaja, brzine i ubrzanja) za sustav druge vrsti prijenosne funkcije otvorene petlje G(s) =(s+1)²/s²(s+2) (ustaljene_pogreske.vsm)

Stabilni sustav trećeg reda s dva pola u ishodištu (Napomena: Da bi bio stabilan trebali smo dodati dvije nule. U protivnom bi sustav bio nestabilan) ima pogrešku ustaljenog stanja položaja i brzine jednaku nuli, a pogreška ubrzanja je konstantna, što znači da će nakon prestanka prelazne pojave izlazni signal s određenim konstantnim kašnjenjem pratiti ulaznu pobudu.

Prijelaz na diskretne sustave je direktan. Neka je W(z) impulsna prijenosna funkcija svih blokova u direktnoj grani (i regulatora i sklopa za obnavljanje i sustava koji se vodi) .

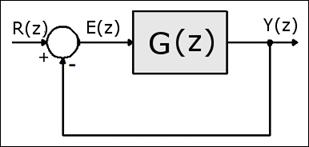
Slika 4.3.6. Jednostavni diskretni regulacijski sustav s negativnom povratnom vezom

Pogreška u z području je

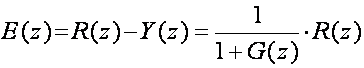(4.3.11)

a po teoremu konačne vrijednosti Z - transformacije imamo

(4.3.12)

pa nakon uvrštavanja dobijemo:

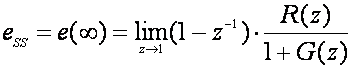(4.3.13)

Pogrešku ustaljenog stanja položaja (ili pomaka) dobijemo tako da uvrstimo Z - transformaciju jediničnog skoka:

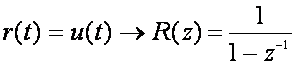(4.3.14)

pa je

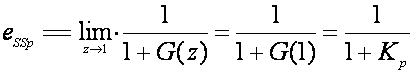(4.3.15)

gdje je K_p konstanta pogreške ustaljenog stanja položaja.

Ukoliko G(z) ima jedan ili više polova u točki z = 1, K_p će biti beskonačan, a pogreška ustaljenog stanja položaja jednaka 0. Ukoliko polova u točki z = 1 nema, pogreška će biti konačna. Kod diskretnih sustava vrijedi tablica na slici 4.3.2 s tim da je kod njih vrst sustava vezana uz broj polova u točki z = 1, s obzirom da se u tu točku preslikavaju polovi iz ishodišta s ravnine.

Pogrešku ustaljenog stanja brzine dobijemo uvrštavanjem u (4.3.13) Z - transformacije jedinične pravčaste uzlazne funkcije:

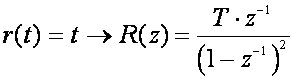(4.3.16)

pa je

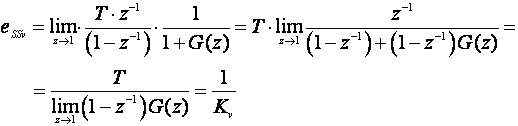(4.3.17)

gdje je K_v konstanta pogreške ustaljenog stanja brzine (Napomena: Zadnji oblik jednadžbe dobili smo tako što smo limes unijeli u brojnik i nazivnik, a limes sume je suma limesa).

Pogreška ustaljenog stanja brzine može biti nula, konačna ili beskonačna, ovisno o tome koliko G(z) ima polova u točki z = 1 (vidi tablicu na slici 4.3.2).

Pogrešku ustaljenog stanja ubrzanja dobijemo uvrštavanjem u (4.3.13) Z - transformacije jedinične kvadratne funkcije:

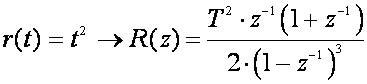(4.3.18)

pa je

(4.3.19)

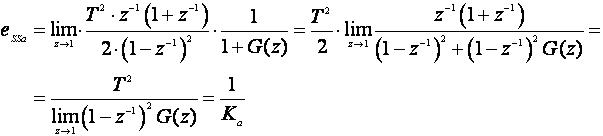
gdje je K_a konstanta pogreške ustaljenog stanja ubrzanja. I ovdje vrijedi tablica na slici 4.3.2.

Iz do sada iznesenog možemo zaključiti sljedeće:

a) Želimo li ukloniti pogreške ustaljenog stanja, odnosno želimo li idealno praćenje referentnog signala, neophodno je da impulsna prijenosna funkcija otvorene petlje sadrži bar jedan pol u točki z = 1. Kako pol u točki z = 1 odgovara polu u ishodištu s ravnine koji određuje integracijsko ponašanje sustava, prethodnu tvrdnju možemo kazati i na sljedeći način: Želimo li ukloniti pogreške ustaljenog stanja, odnosno idealno praćenje referentnog signala, neophodno je da unutar petlje regulacijskog sustava bude bar jedan blok integracijskog ponašanja. Ukoliko sam sustav nema integracijsko ponašanje onda regulator treba imati integracijsku komponentu. Ovo je važna posljedica analize pogreški ustaljenog stanja kojoj ćemo se još vratiti u sljedećem poglavlju. Za sada treba samo zapamtiti da integracijska komponenta regulatora povećava točnost sustava u ustaljenom stanju.

b) Konačna pogreška ustaljenog stanja proporcionalna je periodu uzorkovanja T. Što je T manji, to je i pogreška manja.

Pogledajmo jedan primjer.

Primjer:

Odredi pogreške ustaljenog stanja za sustav čija je prijenosna funkcija otvorene petlje G(z)=0.6/(z-0.4) za T = 0.1.

Sustav je nulte vrsti. Nema pol u točki z = 1 pa mu je pogreška ustaljenog stanja položaja konačna, a pogreške brzine i ubrzanja beskonačne. Pogreška položaje se računa jednadžbom (4.3.14)

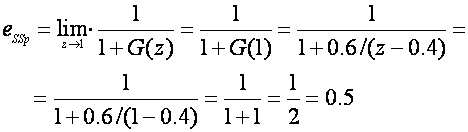
što znači da se odziv sustava u ustaljenom stanju zaustavi na 50% konačne vrijednosti (pogreška ustaljenog stanja je 50%).

Želimo li eliminirati pogrešku trebamo ubaciti regulator koji ima integracijsko ponašanje. Jedan od njih je PI (proporcionalno-integracijski regulator) o kome ćemo detaljno govoriti u poglavlju 5. Za sada kažimo samo to da u z području impulsna prijenosna funkcija PI regulatora glasi

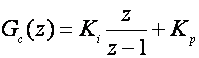
pa sada prijenosna funkcija otvorene petlje

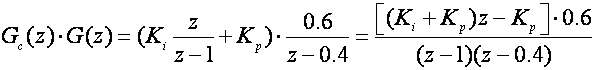
ima pol u točki z = 1, pa je pogreška ustaljenog stanja položaja jednaka 0.

Pogreška ustaljenog stanja brzine je konačna i jednaka

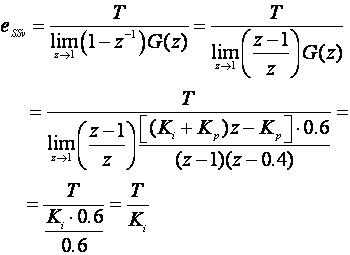
Vidimo da pogreška ustaljenog stanja brzine ne ovisi o proporcionalnoj konstanti regulatora K_p, obrnuto je proporcionalna s integracijskom konstantom K_i, a upravo proporcionalna s periodom uzimanja uzoraka T. Međutim integracijska konstanta se ne smije povećavati iznad vrijednosti za koju sustav postaje nestabilan, a niti se period uzimanja uzoraka smije previše smanjivati.

Pogledajmo ovu situaciju i kroz simulacije u VisSimu. Simulirali smo kontinuirani sustav čija je ekvivalentna impulsna prijenosna funkcija G(z)=0.6/(z-0.4) (radi se o sustavu prijenosne funkcije G(s)=9.1629/(s+9.1629)) vođen diskretnim PI regulatorom i cijeli sustav modeliran u z području čiji smo izlaz diskretizirali kako bi bio uočljiv diskretni karakter odziva. Naravno da su se odzivi u trenucima uzorkovanja poklapali. Slika 4.3.7 prikazuje oba modela u VisSimu i usporedbu referentnog i dobivenog odziva sustava na jedinični pravčasti uzlazni signal (analiziramo konačnu pogrešku ustaljenog stanja brzine) za K_i = 2.

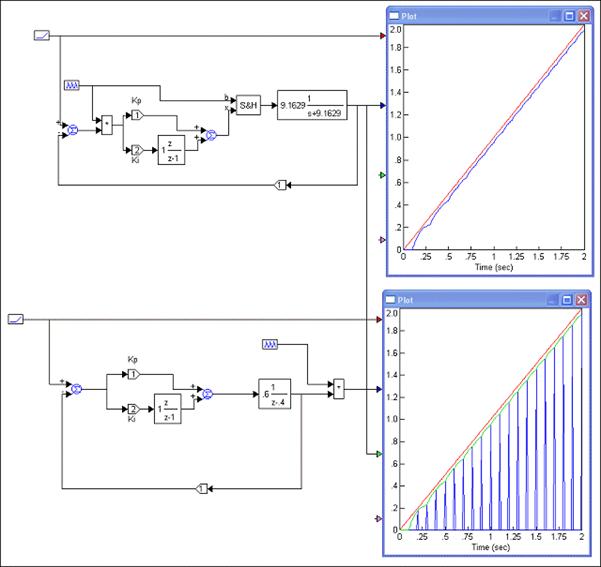
Slika 4.3.7. Dva načina simulacije sustava iz prethodnog primjera – simulacija kontinuiranog sustava vođenog diskretnim regulatorom i simulacija sustava zadanog u z području (K_i = 2 , T = 0.1) (ustaljene_pogreske_2.vsm)

Slika 4.3.8 prikazuje usporedbu situacija za a) K_i = 2, T = 0.1 i b) K_i = 0.5, T = 0.1. Pogreška brzine pada s povećanjem integracijske konstante K_i.

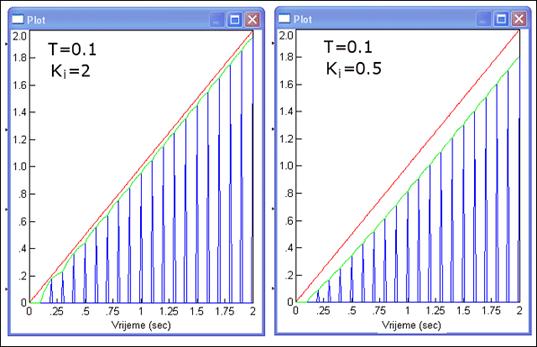
Slika 4.3.8. Pogreška ustaljenog stanja brzine za: a) K_i = 2, T = 0.1 i b) K_i = 0.5, T = 0.1

Analiza točnosti sustava vezana je s vremenskim područjem i pobudnim funkcijama uzlaznog tipa (skok, pravac, parabola). Frekvencijska analiza vezana je sa sinusnim ulaznim pobudama. Frekvencijski dijagram sustava dobijemo tako da na ulaz sustava dovedemo sinusni signal promjenjive frekvencije, te promatramo amplitudu i fazu izlaznog signala koji će kod linearnih sustava također biti sinusan. Kako izračunati i crtati frekvencijske dijagrame sustava i što iz njih možemo zaključiti tema je sljedećeg poglavlja.