4.4. Analiza sustava u frekvencijskoj domeni
Ideja analize je sljedeća. Ulazni signal razvijemo u Fourierov red i prikažemo frekvencijskim spektrima. Na temelju poznavanja frekvencijskih karakteristika sustava u mogućnosti smo za signal svake frekvencije odrediti kolika će biti njegova izlazna amplitude i faza. Kako su sustavi linearni i vrijedi zakon superpozicije moguće je iz frekvencijskog spektra izlaznog signala rekonstruirati njegov vremenski tok.
Međutim bit frekvencijske analize nije u tome da mi rekonstruiramo izlazni vremenski signal. Bit je u tome da se na temelju poznavanja frekvencijske karakteristike otvorenog regulacijskog sustava zaključi kakvo će biti ponašanje zatvorenog regulacijskog sustava, hoće li on biti stabilan, koliko će biti daleko od ruba stabilnosti itd. Frekvencijske dijagrame možemo koristiti i u sintezi regulatora, ali ti se postupci kod diskretnih regulacijskih sustava toliko ne koriste pa ih nećemo niti izučavati.
Frekvencijski dijagrami određeni su frekvencijskom prijenosnom funkcijom koju kod kontinuiranih sustava definiramo kao omjer Fourierove transformacije izlaznog i ulaznog signala:
G(jω) = Y(jω) / X(jω) (4.4.1)
gdje su Y(jω) = F{y(t)} i X(jω) = F{x(t)}. Sam proračun je relativno jednostavan. Poznajemo li prijenosnu funkciju u s području frekvencijsku prijenosnu funkciju dobijemo jednostavnom zamjenom varijable s = jω.
Frekvencijska prijenosna funkcija je kompleksna funkcija koja se crta u ravnini kompleksne funkcije. Frekvencija ω je parametar koji mijenjamo od 0 do ∞. Tako dobiveni frekvencijski dijagram se naziva polarni dijagram. Primjer za sustav prijenosne G(s)=1/(s+5)(s2+2s+2) prikazuje slika 4.4.1.
Na slici je prikazan zatvoreni polarni dijagram poznatiji pod imenom Nyquistov dijagram koji se crta za promjenu kružne frekvencije ω od -∞ do +∞. On u biti odgovara krivulji koja se dobije u ravnini kompleksne funkcije G(s) nakon preslikavanja krivulje koja obuhvaća cijelu desnu polu ravninu ravnine kompleksne frekvencije (s ravnine). U s ravnini mijenjamo varijablu s po imaginarnoj osi od -∞ do +∞ i onda +∞ spojimo s -∞ u beskonačnosti s desne strane. Nyquistov dijagram se praktično crta tako da se nacrta polarni dijagram za pozitivne kružne frekvencije ω (donja krivulja na desnoj strani slike 4.4.1) i onda se ona simetrično ponovi u odnosu na realnu os (gornja krivulja na desnoj strani slike 4.4.1). Ova gornja krivulja odgovara polarnom dijagramu za fiktivne negativne frekvencije ω od 0 do -∞. Ponekad se i osnovni polarni dijagram za promjenu w od 0 do +∞ naziva Nyquistov dijagram za pozitivne frekvencije ili Nyquistov polu-dijagram.
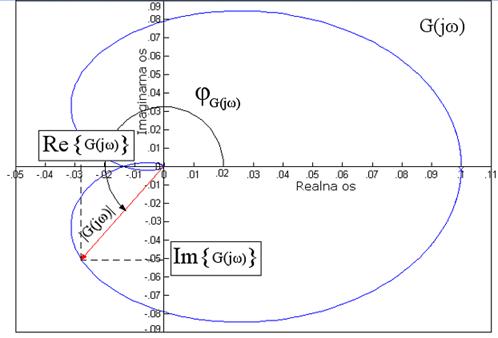
Slika 4.4.1. Nyquistov frekvencijski dijagram prijenosne funkcije G(s)=1/(s+5)(s2+2s+2)
Frekvencijska prijenosna funkcija na frekvenciji ω može se opisati na dva različita načina:
- Realnom i imaginarnom vrijednosti Re{G(jω)} i Im{G(jω)}
- Amplitudom (modulom) i fazom (argumentom) |G(jω)| i φG(jω).
Oba načina opisa povezana su formulama:
![]() (4.4.2)
(4.4.2)
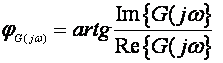 (4.4.3)
(4.4.3)
![]() (4.4.4)
(4.4.4)
![]() (4.4.5)
(4.4.5)
Na slici 4.4.1 frekvencijske dijagrame crtali smo tako da smo na os apscisu stavili Re{G(jω)}, a na os ordinatu Im{G(jω)}. Kazali smo da se takav način crtanja zove polarni dijagram ili Nyquistov polu-dijagram. Međutim to nije jedini način kako se frekvencijska prijenosna funkcija može grafički prikazati. Ukoliko se na apscisu stavi modul |G(jω)|, a na ordinatu argument φG(jω) dobije se Nicholsov dijagram. U ova oba slučaja frekvencija ω je bila parametar. Treći mogući način crtanja je crtati dva dijagrama kod kojih je na apscisne osi stavlja frekvencija ω, a na ordinatne osi kod jednoga amplituda (modul), a kod drugoga faza (argument). Ovakvi dijagrami zovu se Bodeovi dijagrami ili amplitudni i fazni frekvencijski dijagram. Četvrti način crtanja kod kojeg bi na osi apscisa bila frekvencija, a na ordinatama realni i imaginarni dio nema praktične koristi, pa se nikada ne spominje.
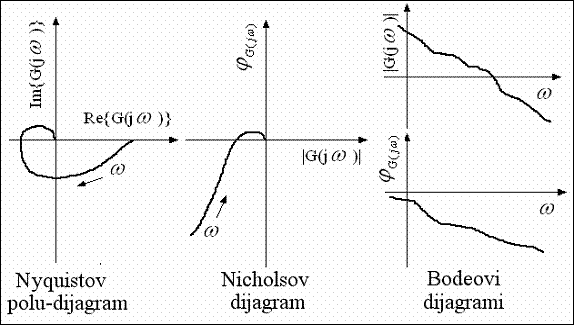
Slika 4.4.2.
Tri uobičajena načina crtanja frekvencijske karakteristike
(Nyquistov polu-dijagram, Nicholsov dijagram i Bodeovi dijagrami)
Prije pojave CAD alata frekvencijski dijagrami su bili nezamjenjivi, kako u analizi, tako i u projektiranju regulacijskih sustava. Danas im je značaj manji, a posebno u analizi i projektiranju diskretnih regulacijskih sustava. Frekvencijski su dijagrami ipak bolje prilagođeni kontinuiranim sustavima. To se posebno odnosi na Nicholsove dijagrame koje zbog toga u nastavku nećemo niti obrađivati. Nyquistovi su dijagrami korisni s edukacijske točke gledanja, pa ćemo se prvenstveno njima i baviti, dok ćemo na koncu kratko spomenuti i Bodeove frekvencijske dijagrame.
U diskretnim sustavima postupak crtanja frekvencijskih dijagrama je sličan s tim da se kreće od impulsne prijenosne funkcije G(z) u kojoj se napravi zamjena z = ejωT :
G(ejωT) = Y(ejωT) / X(ejωT) (4.4.6)
i crtaju se krivulje za frekvencije u osnovnom pojasu što znači da se ωT mijenja od 0 do π, odnosno ω od 0 do π/T. Često se uvodi i supstitucija ω = ωT pa se crta
G(ejω) = Y(ejω) / X(ejω) (4.4.7)
za promjenu ω od 0 do π.
Može se postaviti pitanje zašto se ne vraćamo natrag u s područje inverznom Z - transformacijom pa u s području crtamo frekvencijske dijagrame. Odgovor je: zato što preslikavanje iz z ravnine u s ravninu nije jednoznačno. Cijela z ravnine preslikava se u osnovni pojas s ravnine i sve pojaseve paralelne s njim. Iako to u praksi i nije neki posebni problem, zato što je frekvencija uzorkovanja obično dovoljno velika, tako da se svi polovi i nule nalaze u osnovnom pojasu s ravnine, ipak se često umjesto prelaska iz z ravnine natrag u s ravninu koristi prijelaz iz z ravnine u novu w ravninu primjenom gore spomenute bilinearne transformacije o kojoj govorimo u sljedećem poglavlju.