3.4.2.3. Metoda poklapanja polova i nula
Metoda je isto tako aproksimacijska i temelji se na osnovnoj jednadžbi koja povezuje s i z područje
(3.4.42)
Među svojstvima impulsne prijenosne funkcije spomenuli smo i svojstvo povezanosti polova. Polovi sk od W(s) i od zk od W(z) direktno su povezani jednadžbom oblika (3.4.42), međutim nule nisu. One samo djeluju na konstante pojačanja. Međutim kod ove metode ista se jednadžba koristi i za povezivanje nula prijenosne funkcije W(s) i impulsne prijenosne funkcije W(z).
Ukoliko W(s) ima nule u beskonačnosti W(z) bi trebao dobiti nule u točki z=-1, međutim ponekad se jedna nula od W(z) ostavi u beskonačnosti, čime pridružena jednadžba diferencija dobiva kašnjenje od jednog diskretnog trenutka vremena.
Najveći je problem sa pojačanjem. Obično se aproksimacija radi tako da se poklope pojačanja kontinuiranog i diskretnog sustava za frekvenciju ω=0, odnosno njoj odgovarajuću vrijednost z=1.
Primjer:
Isti primjer kao i prije. Kontinuirani dio sustava je
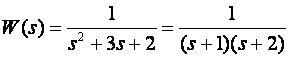
dakle polovi kontinuiranog
sustava W(s) su u točkama s1=-1 i s2=-2, a nula je u
beskonačnosti. Odgovarajući polovi sustava W(z) su u točkama
i 
a nula je u točki -1, pa je impulsna prijenosna funkcija
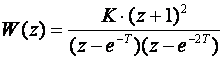
Ostaje još poklopiti pojačanja za s=0 i z=1. Za s=0 G(0)=0.5 pa vrijedi
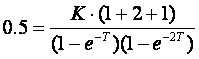
iz čega slijedi
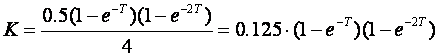
Za T=0.1 vrijedi K = 0.00215626 pa je
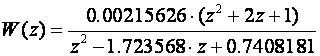
Pretpostavimo li da je jedna od nula impulsne prijenosne funkcije W(z) u beskonačnosti dobiti ćemo:
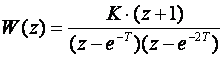
Ostaje još poklopiti pojačanja za s=0 i z=1. Za s=0 biti će W(s)=W(0)=0.5 pa vrijedi
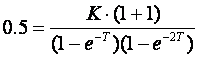
iz čega slijedi
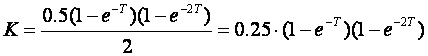
Za T=0.1 vrijedi K = 0.0043125 pa je
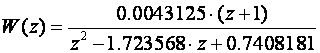
Slika 3.4.10 prikazuje odzive kontinuiranog sustava i diskretnog sustava čija je impulsna prijenosna funkcija dobivena razvojem na parcijalne razlomke ekvivalentne prijenosne funkcije GE(s) i aproksimacijskom metodom poklapanja polova i nula za T=0.1 i to za oba slučaja kada se za obje nule u beskonačnosti prijenosne funkcije W(s) uzme da W(z) ima dvije nule u točki z=-1 i kada se jedna od nula impulsne prijenosne funkcije W(z) ostavi u beskonačnosti, čime se dobiva kašnjenje od jednog diskretnog trenutka vremena.
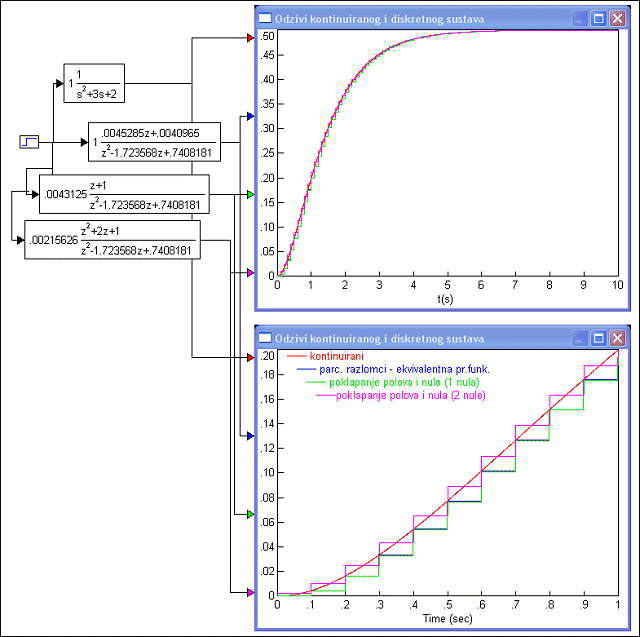
Slika 3.4.10. prikazuje odzive kontinuiranog sustava i diskretnog sustava čija je impulsna prijenosna funkcija dobivena razvojem na parcijalne razlomke ekvivalentne prijenosne funkcije GE(s) i razvojem i aproksimacijskom metodom poklapanja polova i nula za T=0.1 i to za oba slučaja kada su dvije nule od W(z) u točki z=-1 i kada je samo jedna nula od W(z) u točki z=-1 (za objašnjenje vidi tekst) - Diskretizacija_ekvivalentna_i_pole-zero.vsm
Metoda poklapanja polova i nula za slučaj jedne nule u beskonačnosti i razvojem na parcijalne razlomke daje vrlo slične rezultate, a ukoliko usporedimo odzive sa slike 3.4.8 i odziv sustava kod kojeg su obje nule u točki z = -1 također ćemo uočiti sličnost. Razlika bi se pojavila na višim frekvencijama što bi se moglo uočiti iz frekvencijskih dijagrama ovih sustava, a posebno iz faznih dijagrama.