3.4.3. Proračun impulsne prijenosne funkcije složenih sustava sastavljenih od kontinuiranih i diskretnih komponenata
Vratimo se ponovo na situaciju kada se sklop za uzorkovanje nalazi i ispred i iza kontinuiranog sustava prijenosne funkcije G(s).
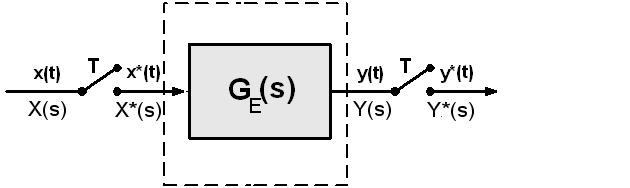
Slika 3.4.11. Blokovski prikaz sustava kod kojeg se uzorkuje ulazna x(t) i izlazna veličina y(t)
Vrijedi
(3.4.43)
gdje je GE(z) Z transformacija prijenosne funkcije GE(s) koja je serijski spoj sklopa za obnavljanje 0-tog reda i kontinuiranog sustava
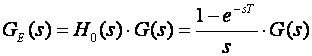(3.4.44)
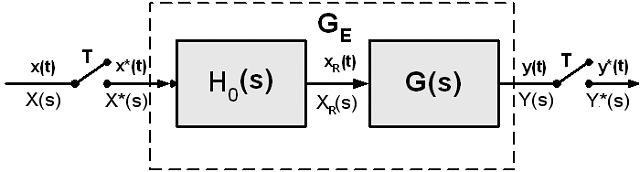
Slika 3.4.12. GE(s) je serijski spoj sklopa za obnavljanje 0-tog reda i kontinuiranog sustava
Već smo prije pokazali da se diskretizacijom izlazne veličine Y(s) dobije
(3.4.45)
odnosno u z području
(3.4.46)
U izrazu (3.4.46) uveli smo novu oznaku H0G(z) koja predstavlja Z - transformaciju serijskog spoja dva kontinuirana bloka – bloka H0 (s) i bloka G(s).
Sada pretpostavimo da se kontinuirani sustav može razbiti na dva serijski spojena bloka G1(s) i G2(s):
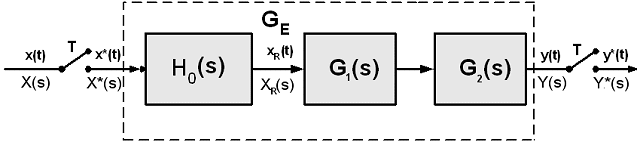
Slika 3.4.13. G(s) je serijski spoj dva kontinuirana bloka
U ovom slučaju pišemo
(3.4.47)
pa je
(3.4.48)
odnosno
(3.4.49)
Ubacimo sada između dva kontinuirana bloka G1(s) i G2(s) novi sklop za uzorkovanje i sklop za obnavljanje:
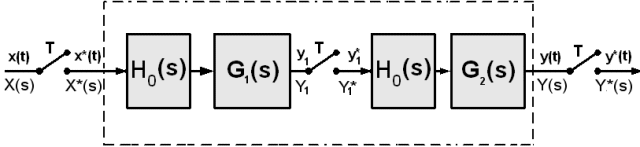
Slika 3.4.14. Situacija u kojoj se ispred svakog kontinuiranog bloka nalazi sklop za uzorkovanje i sklop za obnavljanje
(3.4.50)
(3.4.51)
Diskretizirajmo obje jednadžbe
(3.4.52)
(3.4.53)
odnosno u z području
(3.4.54)
(3.4.55)
pa nakon uvrštavanja dobijemo
(3.4.56)
Dakle impulsna prijenosna funkcija cijeloga sustava jednaka je produktu impulsnih prijenosnih sustava dijelova koji ispred sebe imaju sklop za uzorkovanje. Sklop za obnavljanje nije u ovom dijelu važan, ali kako njega uvijek stavljamo ispred kontinuiranog sustava i ovdje smo ga ubacili.
Usporedimo li ova dva prethodna slučaja važno je zapamtiti da za bilo koje dvije kontinuirane prijenosne funkcije G1(s) i G2(s) Z- transformacija produkta nije jednaka produktu Z - transformacija
(3.4.57)
Pogledajmo jednostavan primjer:
Primjer:
Neka je
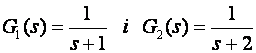
Z – transformacija pojedinih blokova je
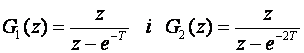
pa je
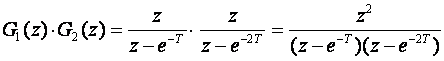
a u jednom od prethodnih primjera smo izračunali
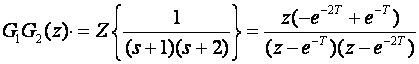
Očito je da
.
Pogledajmo na kraju i situaciju zatvorenog regulacijskog sustava kod kojega je regulator diskretan. Prikazuje ga slika 2.4.6 s tim da ćemo je sada proširiti blokom mjernog pretvarača (eng. Transducer) koji izlazni signal y pretvara u oblik pogodan za diskretizaciju. I on ima svoju prijenosnu funkciju koju ćemo označiti kao H(s).
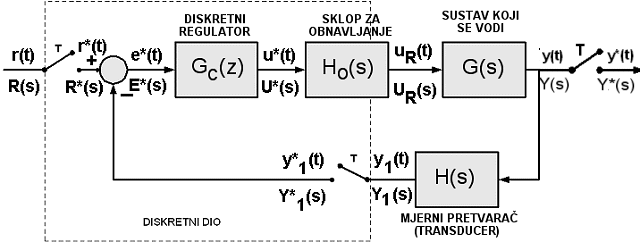
Slika 3.4.15. Situacija u kojoj se ispred svakog kontinuiranog bloka nalazi sklop za uzorkovanje i sklop za obnavljanje
Pišemo
(3.4.58)
(3.4.59)
odnosno nakon diskretizacije
(3.4.60)
(3.4.61)
Kako je
(3.4.62)
(3.4.63)
lako je proračunati
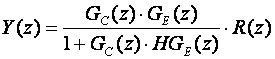(3.4.64)
Specijalni je slučaj kada je H(s)=1. Tada je
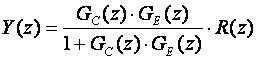(3.4.64)
Ova je jednadžba važna kod projektiranja digitalnog regulatora u diskretnom području o čemu će biti govora u 5. poglavlju.