3.4.4. Parametarska identifikacija impulsne prijenosne funkcije
Postavljanje matematičkog modela sustava uvijek se sastoji od dva koraka:
a) Određivanje strukture matematičkog modela i
b) Proračun parametara matematičkog modela.
Struktura je opći oblik matematičkog modela. Na primjeru prijenosne funkcije postaviti strukturni model sustava je definirati koliko sustav ima polova (red sustava), koliko sustav ima nula i eventualno da li ima i koliko ima polova u nuli (vrst sustava). Na primjer istosmjerni elektromotor upravljan strujom magnetiziranja kome je ulazna varijabla napon U(s), a izlazna kut zakreta Φ(s), uz zanemarivanje trenja u ležajevima i induktiviteta namota, predstavlja se prijenosnom funkcijom prve vrsti, drugog reda bez nula (ima dva pola od kojih je jedan u ishodištu, a u brojniku je samo konstanta pojačanja):
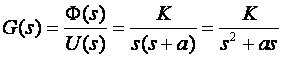
Ovo je strukturni model koji ima dva parametra, konstantu pojačanja K i položaj pola a. Ukoliko poznamo strukturni model sustava parametre možemo relativno lako odrediti postupkom koji se naziva parametarska identifikacija. Naravno nas prije svega zanima parametarska identifikacija impulsne prijenosne funkcije koju u općem obliku prikazujemo
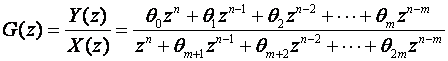(3.4.65)
odnosno nakon dijeljenja s najvećom potencijom varijable z:
