Digitalno vođenje on-line (FESB, Split)

3.4.4.1. Parametarska identifikacija metodom minimalnog kvadratnog odstupanja

Cilj: Pokazati kako se impulsna prijenosna funkcija identificira metodom minimalnog kvadratnog odstupanja odziva sustava dobivenog eksperimentom i simuliranog odziva dobivenog estimiranim parametrima impulsne prijenosne funkcije.

Krećemo od jednadžbe

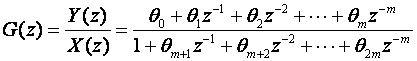(3.4.66)

koju križnim množenjem prebacimo u oblik:

(3.4.67)

Nakon sređivanja dobijemo:

(3.4.68)

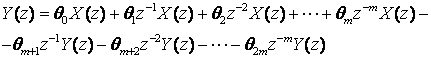
θ₀, θ₁, ..., θ_2msu konstante pa se jednadžba (3.4.68) lako vrati natrag u diskretno područje:

(3.4.69)

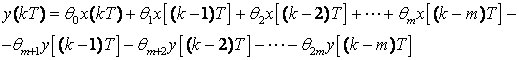
Jednadžbu (3.4.69) možemo napisati i u vektorskom obliku (Napomena: zbog jednostavnosti pisanja ispustili smo period uzorkovanja T):

(3.4.70)

gdje su:

(3.4.71)

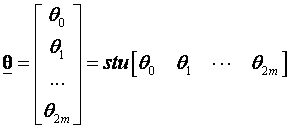(3.4.72)

Formirajmo sada L+1 jednadžbi (L je cijeli broj najmanje jednak 2m – najvećem indeksu nepoznatih parametara koje tražimo), tako da u jednadžbi (3.4.70) napravimo slijedom zamjene k s (k-1), pa s (k-2) sve do (k-L):

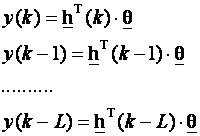(3.4.73)

Jednadžbu (3.4.73) možemo napisati i matrično:

(3.4.74)

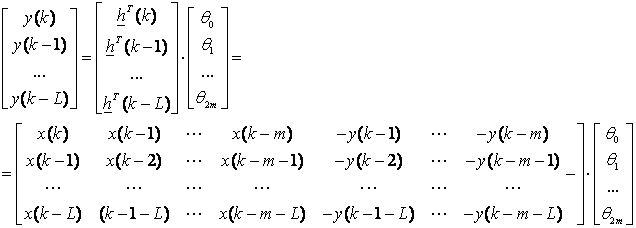
što kraće pišemo:

(3.4.75)

Strategija identifikacije parametara metodom minimalnog kvadratnog odstupanja prikazana je na slici 3.4.16.

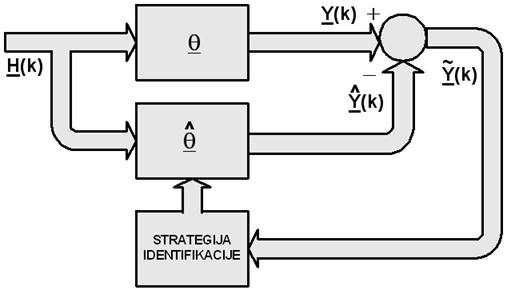
Slika 3.4.16. Strategija identifikacije parametara metodom minimalnog kvadratnog odstupanja

Ista sekvenca ulazno - izlaznih signala množi se s točnim parametrima (jednadžba (3.4.75)) i pretpostavljenim (estimiranim) parametrima

(3.4.76)

Razlika

(3.4.77)

je pogreška izlaza. Zadatak postupka identifikacije je odrediti vektor pretpostavljenih parametara tako da suma kvadratnog odstupanja pogreške izlaza za različite diskretne trenutke vremena bude minimalna. Matematički to iskazujemo ciljnom funkcijom oblika:

(3.4.78)

gdje je W(k) pozitivno definitna težinska matrica (obično dijagonalna) kojom iskazujemo značaj pojedinog diskretnog trenutka za proračun parametara impulsne prijenosne funkcije:

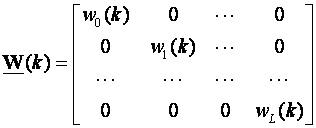(3.4.79)

W(k) je najčešće jedinična matrica, ali w_i(k) može biti i primjerice oblika w_i(k)=μ^k-L+i. μ je proizvoljna konstanta, ali ukoliko su nam važniji stariji podaci tada μ treba biti veći od jedinice, a ukoliko su važniji noviji podaci tada μ treba biti manji od jedinice.

Jednadžba (3.4.78) ima minimum za

(3.4.80)

Kako je ovaj izraz važan pokažimo kako se do njega dolazi.

Dokaz jednadžbe (3.4.80) :

Uvrstimo (3.4.77), (3.4.76) i (3.4.75) u (3.4.78):

(3.4.81)

Dalje slijedi:

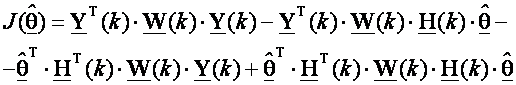(3.4.82)

Kako je matrica uvijek pozitivno semidefinitna (nenegativno definitna) funkcija ima minimum. U svrhu dokaza na kraju izraza ćemo dodati i oduzeti jedan član:

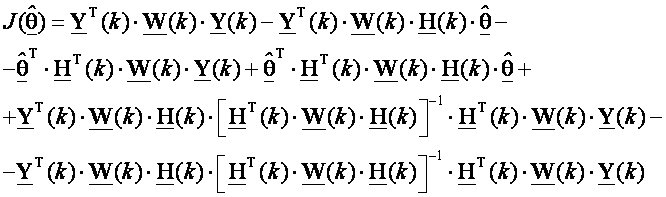(3.4.83)

Vrijedi

pa (3.4.83) možemo napisati u obliku:

(3.4.84)

Izraz (3.4.84) ima minimum po onda kada je drugi član sume na desnoj strani jednak nuli a iz toga slijedi da je to ispunjeno onda kada je

Time smo dokazali jednadžbu (3.4.80).

Ilustrirajmo postupak primjerom.

Primjer

Zadatak nam je identificirati impulsnu prijenosnu funkciju jednostavnog RC kruga čiji spoj znamo, ali ne znamo vrijednosti komponenata. Na ulaz RC kruga preko D/A pretvarača dovodimo sekvencu proizvoljnih signala generiranih računalom, a istovremeno preko A/D pretvarača u računalo spremamo diskretni slijed izlaznih signala. Situaciju shematski prikazuje slika 3.4.17.

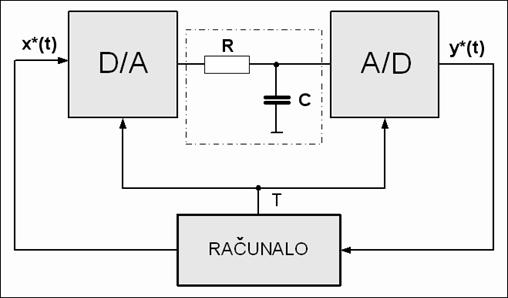
Slika 3.4.17. Parametarska identifikacija impulsne prijenosne funkcije (primjer)

Slijed ulaznih i izlaznih signala u diskretnim trenucima vremena dan je u sljedećoj tablici :

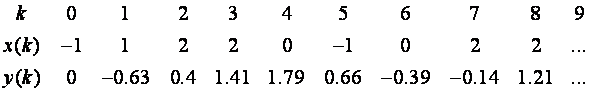
Prvi nam je korak odrediti oblik impulsne prijenosne funkcije. Prijenosna funkcija RC mreže je

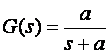
gdje je a=1/RC. Ispred RC mreže nalazi se D/A pretvarač (sklop za obnavljanje 0-tog reda) što znači da identificiramo impulsnu prijenosnu funkciju ekvivalentnog sustava. Tablice na slici 3.4.6 to upravo daju:

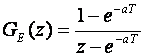
Nakon množenja brojnika i nazivnika sa z^-1 dobijemo:

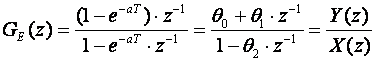
gdje su . Zadatak nam je odrediti parametre s tim da nam spoznaja da je dođe kao odlična provjera postupka identifikacije parametara. Iz jednadžbe slijedi:

odnosno u diskretnom području:

Najveći indeks nepoznatih parametara je 2, pa je L=2. Za trenutak u kojemu provodimo identifikaciju odabiremo proizvoljni diskretni trenutak k=4, pa formiramo sve potrebne matrice i vektore:

Jednadžba (3.4.80) daje:

pa nepoznata impulsna prijenosna funkcija glasi:

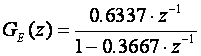
Napomena: Treba uočiti da se kod proračuna impulsne prijenosne funkcije nigdje ne javlja period uzimanja uzoraka T, međutim on je važan zbog dva razloga. Prvi je taj što nam on treba ukoliko bismo iz impulsne prijenosne funkcije htjeli odrediti parametre kontinuirane prijenosne funkcije (parametar a=1/RC). Drugi je razlog još važniji. Naime ukoliko na temelju ove impulsne prijenosne funkcije projektiramo diskretni regulator on će zadovoljavati samo ukoliko period uzorkovanja sustava vođenja bude jednak ovom periodu uzorkovanja za koji smo radili identifikaciju. Za neki drugi period uzorkovanja parametri impulsne prijenosne funkcije bi bili drugačiji, pa bi i parametri regulatora bili drugačiji.

Ukoliko nismo zadovoljni postignutom točnosti u proračun možemo uključiti i sljedeće diskretne trenutke vremena te postupak proračuna napraviti rekurzivnim o čemu se govori u sljedećem poglavlju.