Digitalno vođenje on-line (FESB, Split)

3.4.4.2. Rekurzivni postupak estimacije parametara metodom minimalnog kvadratnog odstupanja

Cilj: Naučiti kako parametre impulsne prijenosne funkcije možemo proračunati još točnije koristeći rekurzivni postupak.

Želimo li još točnije proračunati nepoznate parametre impulsne prijenosne funkcije možemo primijeniti rekurzivni postupak estimacije parametara metodom minimalnog kvadratnog odstupanja (eng. Recursive Least-Square Estimation). Kako je dokaz malo složeniji ovdje ga navodimo bez dokaza i čitatelje upućujemo na literaturu (npr. K.J. Ǻström, B. Wittenmark, Computer-Controlled Systems, Prentice-Hall Int. Edition, 1990).

Uzevši u obzir i prvi sljedeći trenutak (k+1) parametri se mogu još točnije proračunati koristeći jednadžbu:

(3.4.85)

gdje su:

y(k+1) i w(k+1) su skalari, a

(3.4.86)

(3.4.87)

Primjer:

Izračunajmo za prethodni primjer novu estimaciju parametara uzevši vrijednosti za k=5:

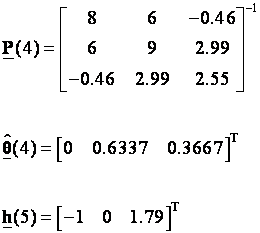
pa je

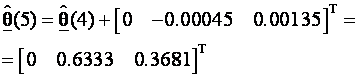
Postupak se može nastaviti za k=6 itd, iako će doprinos točnoj vrijednosti parametara biti sve manji i manji. U prethodnom primjeru točna vrijednost parametara je bila , pa je već i prva estimacija bila dovoljno dobra.

Nedostatak ove metode je taj što je izlaznom signalu najčešće superponiran i signal šuma kako to zorno prikazuje slika 3.4.18.

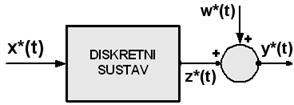
Slika 3.4.18. Diskretni sustav sa superponiranim signalom šuma

Izlaznom signalu iz diskretnog sustava superponiran je šum w(kT) (koji može biti bijeli, Gaussov šum, ali i ne mora):

(3.4.88)

Parametarska identifikacija metodom minimalnog kvadratnog odstupanja daje dobar rezultat samo ukoliko je signal šuma zanemariv. Ukoliko šum postoji metoda zahtjeva jako veliki broj ulazno – izlaznih parova (1000 i više) kako bi se dobio koliko – toliko dobar rezultat.

Uz prisustvo šuma bolje rezultate daju neke druge metode npr. metoda maksimalne sličnosti (eng. MLE - Maximum Likehood Estimation) ali njena analiza prelazi okvire ovog uvoda pa čitatelje upućujemo na literaturu (npr. G.N. Saridis, Comparison of Six On-line Identification Algorithms, Automatica 10, 1974, 69-79 ). Napomenimo samo da se u postupku obično pretpostavi da je šum bijeli, Gaussov, te se postavlja jednadžba za (L+1) dimenzionalnu funkciju združene gustoće vjerojatnosti i traženja vektora koji će je maksimirati.

Nas obično zanima kako će se određeni sustav koji smo opisali impulsnom prijenosnom funkcijom ponašati, kakav će mu biti odziv ukoliko mu na ulaz dovedemo određenu pobudu. Sljedeće se poglavlje bavi tim problemom.