3.4.5. Vremenski odziv diskretnog sustava opisanog impulsnom prijenosnom funkcijom
Odziv sustava u z području računa se kao produkt impulsne prijenosne funkcije ekvivalentnog sustava i Z - transformacije ulaznog signala (jednadžba (3.4.18)):
![]() (3.4.89)
(3.4.89)
Pretpostavimo da je GE(z) poznat u faktoriziranom obliku
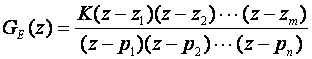 (3.4.90)
(3.4.90)
gdje su z1 do zm nule, a p1 do pn polovi impulsne prijenosne funkcije. X(z) je Z - transformacija ulaznog signala (pobude) koja je u općem slučaju također racionalna funkcija varijable z koju također možemo prikazati u faktoriziranom obliku:
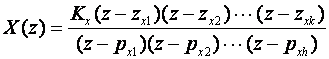 (3.4.91)
(3.4.91)
X(z) ima k nula i h polova. Za realne sustave vrijedi m ≤ n i k ≤ h. Kako bi analiza bila jednostavnija pretpostaviti ćemo da se polovi i nule ekvivalentne impulsne prijenosne funkcije i ulaznog signala ne poklapaju (iako se u općem slučaju i to može dogoditi). Razbijemo li Y(z)/z na parcijalne razlomke dobijemo
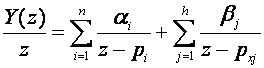 (3.4.92)
(3.4.92)
Drugi sumator uključuje sve pobudne funkcije. Na primjer za skokovitu ulaznu pobudu vrijedi X(z)=z/(z-1) pa drugi sumator ima samo jedan član β/(z-1). Na taj dio ne možemo ni na koji način utjecati. Prvi sumator uključuje doprinos samog sustava. Svaki pol u točki pi doprinosi odzivu sustava za αi.z/(z-pi) (Napomena: Kako bi dobili Y(z) lijevu i desnu stranu smo ponovo množili sa z).
Tablica na slici 3.3.1, uz napomenu da je pi=e-aT i a=-ln(pi)/T, daje doprinos ovog pola odzivu sustava. On iznosi αi. (pi)k. Važno je uočiti da ovaj član teži 0 kada k teži u beskonačno, onda i samo onda ukoliko je |pi| <1. U tom slučaju svi članovi koji pripadaju polovima impulsne prijenosne funkcije ne utječu na odziv sustava u stacionarnom stanju. Na njega utječe samo drugi dio koji pripada ulaznom signalu. Ovo je važan rezultat koji ćemo koristiti u poglavlju 4.1 gdje analiziramo stabilnost diskretnih sustava.
Ukoliko nema ulazne pobude odziv sustava obično nazivamo slobodni odziv, dosta važan u analizi diskretnih sustava. O njemu detaljno govorimo u poglavlju 4.3.
Ukoliko poznajemo vremenski slijed ulaznog signala x(0), x(T), x(2T), …, vremenski odziv diskretnog sustava opisanog impulsnom prijenosnom funkcijom možemo dobiti i direktno koristeći teorem vremenskog pomaka Z - transformacije. Pri tome je nužno u izrazu (3.4.90) pomnožiti sve faktore brojnika i nazivnika, te impulsnu prijenosnu funkciju sustava prikažemo razlomljenom racionalnom funkcijom varijable z:
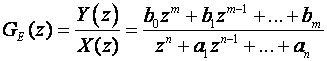 (3.4.93)
(3.4.93)
Sljedeći korak je dijeljenje brojnika i nazivnika najvećom potencijom varijable z, a to je za realne sustave zn:
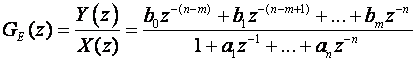 (3.4.94)
(3.4.94)
Sada križno množimo dva desna razlomka:
![]() (3.4.95)
(3.4.95)
iz čega slijedi:
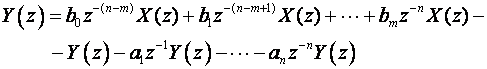 (3.4.96)
(3.4.96)
Primjenom teorem vremenskog pomaka Z - transformacije dobijemo:
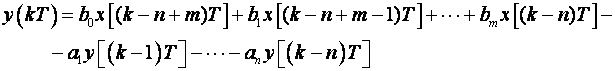 (3.4.97)
(3.4.97)
Odziv se računa iteracijski, u svakom sljedećem trenutku koriste se rezultati dobiveni u prethodnom. Pri tome trebamo poznavati vremenski slijed pobudnog signala u svim diskretnim trenucima vremena i za sustav n-tog reda n početnih uvjeta.
Primjer:
Trebamo izračunati odziv sustava iz prvog dijela ovog poglavlja (poglavlje 3.) prikazanog na slici 3.3 ako je Kp = 10, Ks = 1 , T = 0.02 i y(0) = 0, a pobuda je jedinični skok
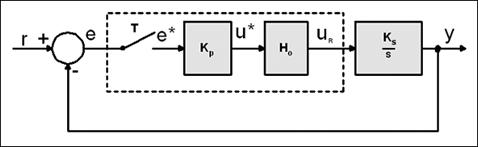
Slika 3.3. Integracijski sustav vođen diskretnim proporcionalnim regulatorom
Računamo:
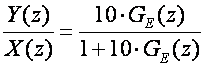
gdje je (tablica na slici 3.4.6 )
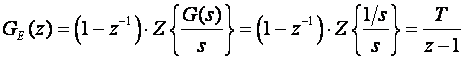
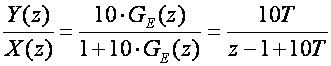
Nakon uvrštavanja T = 0.02 dobijemo
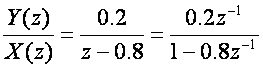
pa je
![]()
odnosno
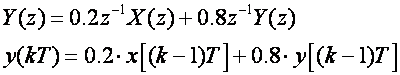
Dalje je jednostavno:
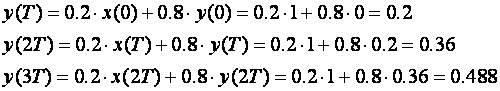
itd.
Pogledamo li sliku 3.4 lako ćemo uočiti da se proračunate vrijednosti podudaraju s rezultatima simulacije.