3.4.6. Proračun odziva sustava između dva trenutka uzorkovanja
Odgovor na ovo pitanje već smo dali, ali ga nismo posebno naglasili. Jednadžba (3.4.14) koju ovdje ponavljamo
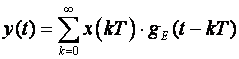 (3.4.14)
(3.4.14)
daje kontinuirani izlaz sustava y(t) kao produkt vrijednosti ulaznog signala u trenutku kT i karakterističnog odziva ekvivalentnog sustava (inverzne Laplaceove transformacije prijenosne funkcije). Ilustrirajmo to na primjeru diskretnog regulacijskog sustava s negativnom povratnom vezom.
Primjer:
Regulacijski sustav je prikazan na slici 3.4.19.
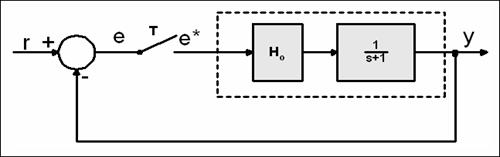
Slika 3.4.19. Diskretni regulacijski sustav
Na ulazu je jedinična odskočna funkcija r(t)=u(t). Zbog preglednosti pisanja pretpostavimo da je T = ln(2).
Impulsna prijenosna funkcija ekvivalentnog sustava je
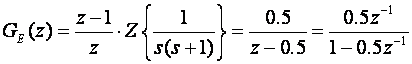
Sa slike je očito da je
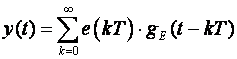
gdje je e(kT) vrijednost pogreške r(kT) - y(kT) u trenutku kT. Računamo
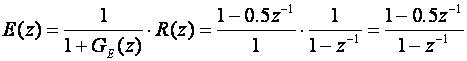
Inverzna Z - transformacija daje
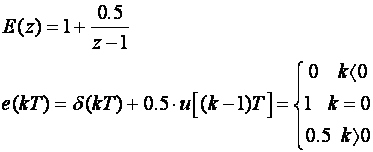
Sljedeći je proračun karakterističnog odziva ekvivalentnog sustava
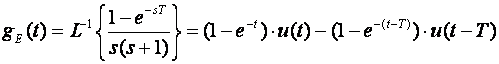
Sada možemo proračunati odziv sustava
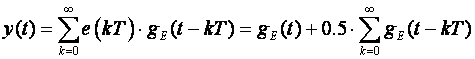
Za 0 < t < T imamo samo
![]()
a za t > T imamo
![]()
U našem specifičnom odabiru T = ln (2) slijedi eT = 2 pa je za t > T
![]()
Naravno da je do ovog rezultata puno lakše doći simulacijom. Rezultate simulacije u VisSimu za ovaj isti primjer i T=ln(2)= 0.693147 pokazuje slika 3.4.20. Simulacijsko vrijeme je bilo 100 puta veće. Promijenimo li period uzorkovanja na T=0.5 rezultat je drugačiji i prikazuje ga slika 3.4.21.
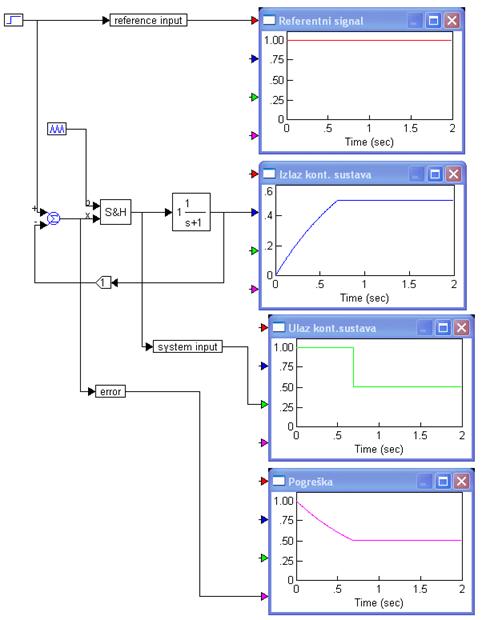
Slika 3.4.20. Simulacija odziva sustava sa slike 3.4.19 za
T=ln(2)=0.693147
(vremenski_odziv.vsm)
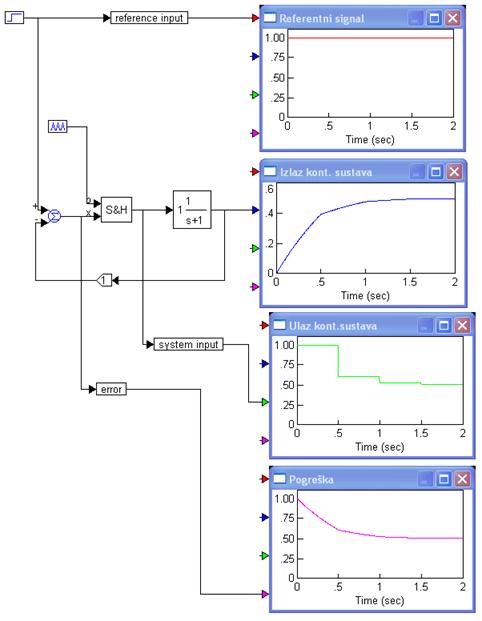
Slika 3.4.21. Simulacija odziva sustava sa slike 3.4.19 za T= 0.5