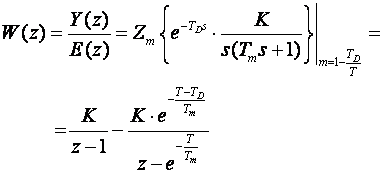3.4.7. Proračun odziva sustava između dva trenutka uzorkovanja pomoću modificirane Z - transformacije
Što se događa između dva perioda uzorkovanja možemo doznati i ukoliko umjesto Z – transformacije koristimo modificiranu Z – transformaciju. Temelji se na tome da se uvodi još jedna nova varijabla pomoću koje možemo istraživati što se događa između dva perioda uzorkovanja. Novom varijablom možemo ispitivati što se događalo u prethodnom intervalu između kT i (k-1)T ili što će se događati u sljedećem intervalu između kT i (k+1)T. U prvom slučaju varijablu obično nazivamo m varijabla, a transformaciju modificirana Zm - transformacija, dok se u drugom slučaju radi o varijabli μ i modificiranoj Zμ - transformaciji. Slika 3.4.22 pokazuje dio vremenske osi i način definiranja dodatnih varijabli m i μ .
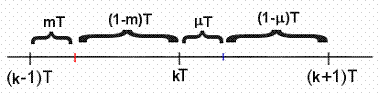
Slika 3.4.22. Način definiranja varijabli m i μ modificirane Z - transformacije
Jednadžbe za proračun modificirane Z - transformacije su jednostavne i svode se na to da se iz trenutka kT pomaknemo u trenutak [kT – (1-m)T] za Zm - transformaciju odnosnu u trenutak [kT + μT] za Zμ - transformaciju:
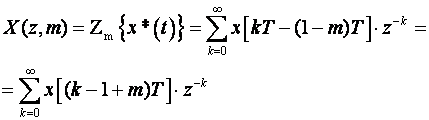(3.4.98)
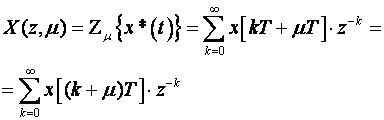(3.4.99)
U prvom slučaju m transformacije modificirana Z - transformacija nije ništa drugo nego Z - transformacija pomaknutog signala prema prethodnom diskretnom trenutku, a u drugom slučaju prema budućem diskretnom trenutku. Lako je pokazati da vrijede sljedeće jednakosti (vidi sliku 3.4.22):
(3.4.100)
(3.4.101)
(3.4.102)
(3.4.103)
Modificirana Z - transformacija ima ista svojstva kao i obična Z - transformacija, a računa se također korištenjem tablica. Slika 3.4.23 prikazuje neke osnovne transformacije.
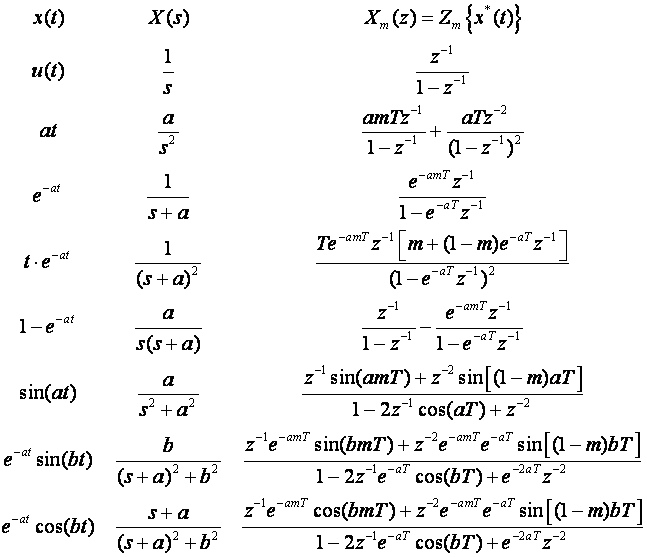
Slika 3.4.23.
Tablice modificirane Z - transformacije
Pojavom simulacijskog softvera modificirana Z - transformacija nije više toliko značajna (vidi poglavlje 3.4.6), pa se s njom više nećemo niti baviti, osim što ćemo postupak korištenja tablica ilustrirati jednim primjerom koji zorno ilustrira kako i na koji dio sustava primijeniti modificiranu Z - transformaciju.
Primjer:
Za sustav sa slike izračunaj izlazni signal i između diskretnih trenutaka uzorkovanja koristeći Zm - transformaciju ako je T=0.5.
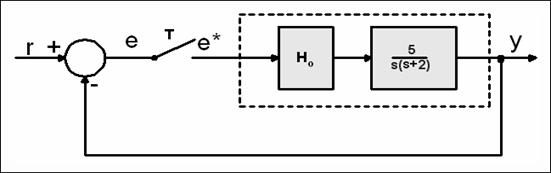
Slika 3.4.24. Diskretni regulacijski sustav za koji računamo odziv koristeći modificiranu Z - transformaciju
Na ulaz ekvivalentnog sustava dovodimo diskretni signal e*(t) signala pogreške e(t). Prema slici možemo u s području pisati:
Nakon diskretizacije i prelaska u z područje (vidi poglavlje 3.4.3) dobijemo
Za signal na ulazu ekvivalentnog sustava e* nije važno što se događa između diskretnih trenutaka vremena zato što je on izlazni signal sklopa za uzorkovanje, pa se zato kod njegovog proračuna koristi obična Z - transformacija ekvivalentnog sustava. Ona daje ispravne vrijednosti u trenucima uzorkovanja i to je za proračun e* jedino važno. Izlaz sustava se u s području računa jednadžbom
Ukoliko nas zanima samo što se događa u trenucima uzimanja uzoraka i ovu jednadžbu jednostavno diskretiziramo i prebacimo u z područje
ali ukoliko nas zanimaju i događanja između diskretnih trenutaka uzimanja uzoraka ekvivalentnu prijenosnu funkciju trebamo u z područje prebaciti modificiranom Z - transformacijom:
Uvrstimo li izraz za E(z) dobijemo
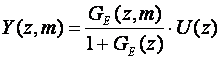
Tablice nam daju:
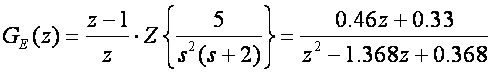
i
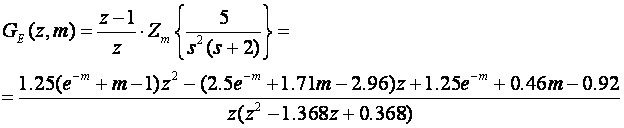
Nakon uvrštavanja dobijemo izraz za proračun Y(z,m):
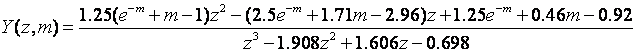
Dijeljenjem brojnika i nazivnika izračunamo:
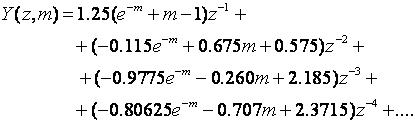
iz čega direktno slijede vrijednosti izlaza u diskretnim trenucima vremena 0, T, 2T, 3T, 4T itd.
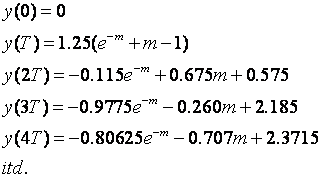
Za m=1 vrijednost odgovara tom diskretnom trenutku vremena (vidi sliku 3.4.22), a za m=0 prethodnom trenutku što je lako provjeriti. Za bilo koji trenutak između uvrsti se odgovarajuća vrijednost varijable m. Na primjer za y(T) i diskretne vrijednosti varijable m=0, 0.2, 0.4, 0.6, 0.8 i 1 dobijemo: y(T,m=0)=y(0)=0, y(T,m=0.2)=y(0.2T)=0.0234, y(T,m=0.4)=y(0.4T)=0.879, y(T,m=0.6)=y(0.6T)=0.186, y(T,m=0.8)=y(0.8T)=0.3117 i y(T,m=1)=y(T)=0.4600. Slika 3.4.25 pokazuje rezultate simulacije koji se u potpunosti slažu s proračunom.
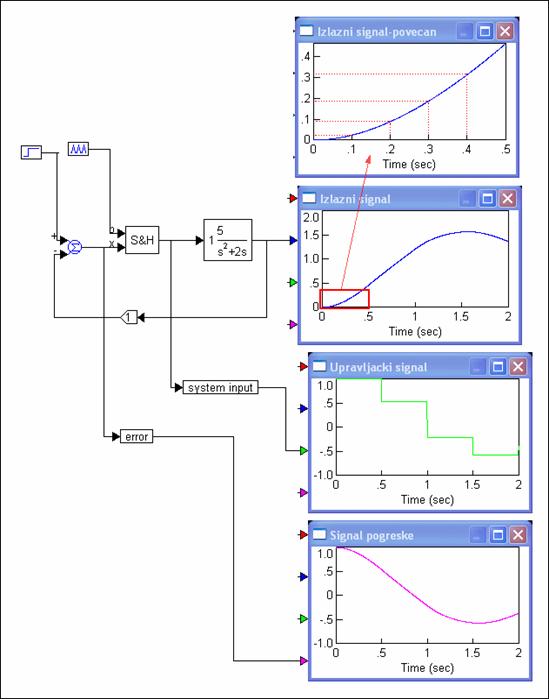
Slika 3.4.25. Simulacija odziva sustava sa slike 3.4.24 za T=0.5
Napomena: Ovaj je primjer važan kako bi se uočilo da se izlaz sustava računa jednadžbom
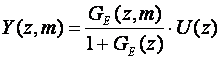
a ne jednadžbom
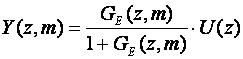
kod koje je i u brojniku i u nazivniku modificirana Z - transformacija ekvivalentnog sustava. Ovo je česta pogreška.
Modificirana Z - transformacija je korisna i ukoliko postoji u vremenskoj domeni pomak signala x(t) koji nije jednak cjelobrojnom višekratniku perioda uzorkovanja. Pomak možemo iskazati izrazom
(3.4.105)
gdje su T period uzimanja uzoraka N
cijeli broj, a 
vrijednost manja od perioda uzimanja uzoraka. Pomak m
se u ovom slučaju računa
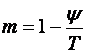(3.4.106)
Modificirana Z - transformacija pomaknutog signala je
(3.4.107)
Primjer
Diskretiziraj
signal 
pomaknut za 0.35 ako je T=0.1. Signal možemo prikazati
produktom funkcije i pomaknutog jediničnog skoka
Vrijedi
iz čega slijedi da je m=0.5.
Primijenimo na signal
modificiranu Z - transformaciju:
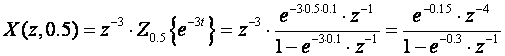
Podijelimo li brojnik i nazivnik dobijemo
što u vremenskoj domeni daj
Slika 3.4.26 prikazuje pomaknuti kontinuirani signal i diskretne vrijednosti za T=0.1. Modificirana Z - transformacija je dala ispravne rezultate.
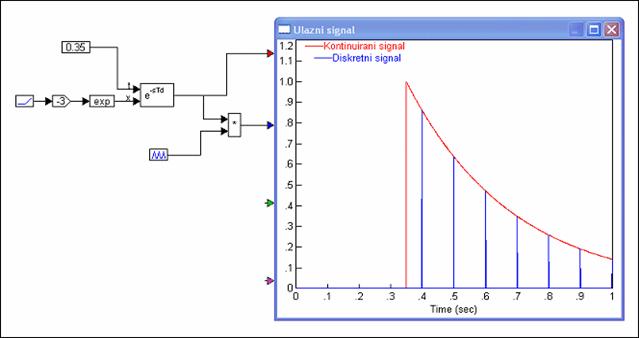
Slika 3.4.26. Pomaknuti kontinuirani i diskretizirani signal
za slučaj kada pomak nije cjelobrojni višekratnik perioda uzorkovanja
(T=0.1)
(diskretizacija_sa_pomakom.vsm)
Treći primjer upotrebe modificirane Z - transformacije je analiza sustava koji ima transportno kašnjenje.
Primjer
Slika 3.4.27 prikazuje jedan takav slučaj – sustav drugog reda prve vrsti (na primjer istosmjerni elektromotor upravljan strujom magnetiziranja kod kojeg smo zanemarili trenje u ležajevima i induktivitet namota) kod kojeg je ulazni signal zakašnjen za vrijeme TD.
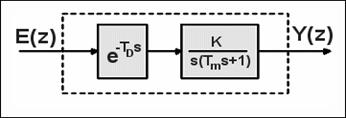
Slika 3.4.27. Diskretni regulacijski sustav za koji računamo
odziv koristeći modificiranu Z - transformaciju
Impulsna prijenosna funkcija ovog serijskog spoja je
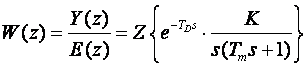
što možemo izračunati koristeći modificiranu Z - transformaciju
