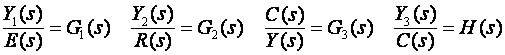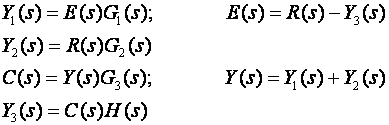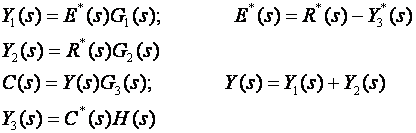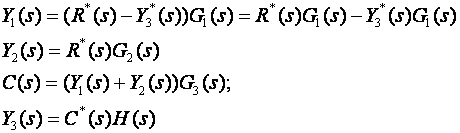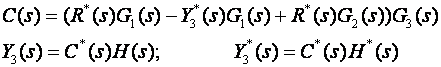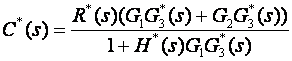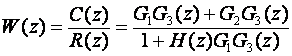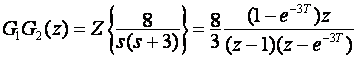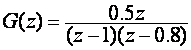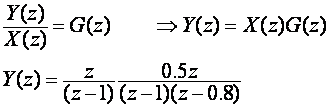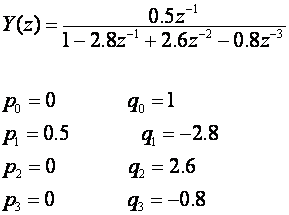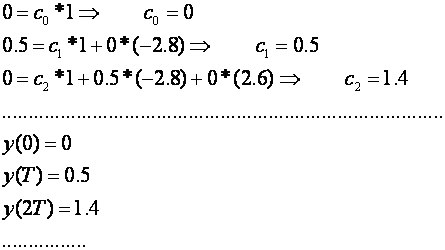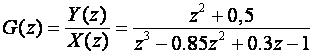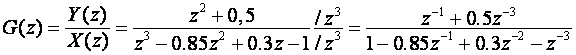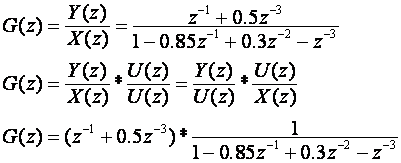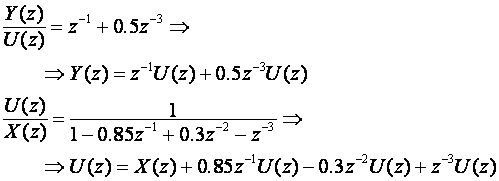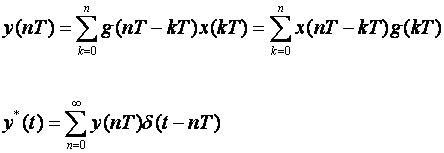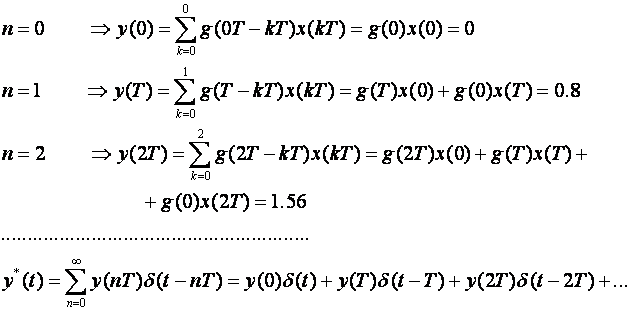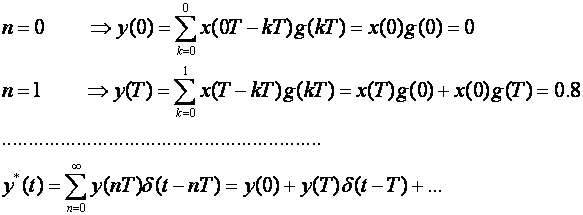Digitalno vođenje on-line (FESB, Split)

3.4.8. Zadaci

1. Analiza uzorkovanih složenih regulacijskih sustava temeljena na blok prikazima elemenata sustava

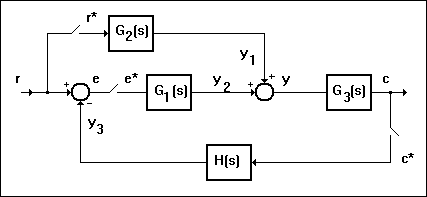
Na slici 3.4.28 prikazan je sustav kod kojeg je u regulacijskoj petlji povezano više elemenata, svaki opisan vlastitom prijenosnom funkcijom. Sklopovi za uzorkovanje djeluju sa jednakim vremenom uzorkovanja T i nalaze se na točno određenim mjestima. Odrediti impulsnu prijenosnu funkciju zatvorene regulacijske petlje ili W(z)=?

Slika 3.4.28. Regulacijski sustav složen od niza elemenata

Svaki element regulacijske petlje opisan je vlastitom prijenosnom funkcijom koja povezuje signale na ulazu i izlazu elementa. Tako u kontinuiranom području, prema blokovima i uvedenim pomoćnim signalima na slici Z3-7 vrijedi:

ili

Budući da u regulacijskoj petlji postoji više mjesta na kojima se uzorkuju signali, potrebno je uzorkovanje unijeti u matematički opis ili

Nakon što se u matematički opis unesu i mjesta uzorkovanja, mogu se korak po korak eliminirati pomoćni signali ili

dalje,

povezujemo još dvije preostale relacije,

ili

Da bi u posljednjoj relaciji mogli povezati signale, potrebno je cijeli izraz uzorkovati. Pri tome već uzorkovani dijelovi takvi i ostaju. Uzorkuju se samo oni koji su još kontinuirani.

Poseban komentar!

Završno uzorkovanje dovodi do situacije da se dva bloka uzorkuju zajedno tj. prolaze kroz sklop za uzorkovanje tek nakon što se serijski povežu. Tako treba i napisati matematički model. Kod diskretnih sustava vrijedi upamtiti:

Obično kraće pišemo,

Konačno, posljednja relacija glasi:

ili

Na temelju analize složenog sustava i sklopova za uzorkovanje koji se nalaze na zadanim mjestima unutar regulacijske petlje, možemo napisati impulsnu prijenosnu funkciju zatvorene petlje zadanog sustava, ili

Dokaz komentara!

Uvedeni komentar može se jednostavno i dokazati. Ako su dva jednostavna bloka povezana serijski i ako nakon njih slijedi sklop za uzorkovanje, vrijedi:

G1 (s)G2 (s) / * = G1 G2 * (s) = G1 G2 (z)

uz ,

Da smo u ovom slučaju tražili Z - transformaciju svakog pojedinog člana dobili bi:

, što daje

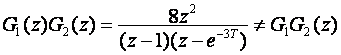
Ovaj oblik Z - transformacije dva serijski povezana bloka bio bi točan u slučaju kad bi se sklopovi za uzorkovanje nalazili iza svakog bloka.

Problem različitih interpretacija dva serijski povezana bloka i načina njihovog prolaska kroz sklopove za uzorkovanje ne očituje se samo u različitim Z - transformacijama, već i u izrazito različitim odzivima koje daju. Ako dva bloka uvedena u ovom dokazu povežemo na dva različita načina u odnosu na sklopove za uzorkovanje i na njih dovedemo jediničnu odskočnu funkciju, odzivi će biti, prema slici 3.4.29, potpuno različiti.

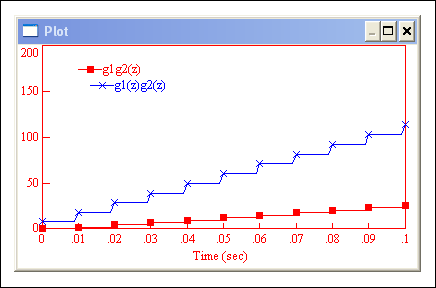
Slika 3.4.29. Odzivi na odskočnu funkciju za dva načina povezivanja i uzorkovanja elementarnih blokova u serijskoj vezi

2. Odziv sustava na zadanu pobudu na temelju poznate impulsne prijenosne funkcije

Diskretni sustav opisan je impulsnom prijenosnom funkcijom G(z). Ulazni je signal također opisan pomoću Z – transformacije. Odrediti Z - transformaciju odziva sustava i vrijednosti tri uzorka odziva.

Poznata je impulsna prijenosna funkcija:

Ulazni signal je zadan pomoću Z – transformacije, tj.

Budući da impulsna prijenosna funkcija predstavlja omjer izlaznog i ulaznog signala u z području, odziv sustava određuje se kao:

Na taj način se može prikazati Z – transformacija odziva. Uzorci odziva dobiju se pomoću inverzne Z – transformacije i to odabranom metodom, npr. pomoću Juryjevih koeficijenta.

Vrijedi:

3. Priprema za sklopovsku izvedbu i simulaciju impulsne prijenosne funkcije pomoću osnovnih komponenti

Diskretni sustav opisan je impulsnom prijenosnom funkcijom G(z). Simulirati impulsnu prijenosnu funkciju i pripremiti je za sklopovsku izvedbu primjenom osnovnih simulacijskih elemenata za diskretno područje (sklopovi za kašnjenje, zbrajala i množila s konstantom).

Da bi se koristili sklopovi za kašnjenje, potrebno je impulsnu prijenosnu funkciju i izraziti pomoću njih, pa vrijedi:

Da bi se jednostavnije objasnio oblik pogodan za simulaciju (i sklopovsku izvedbu), provode se dopuštene matematičke preinake ili

Vrijedi:

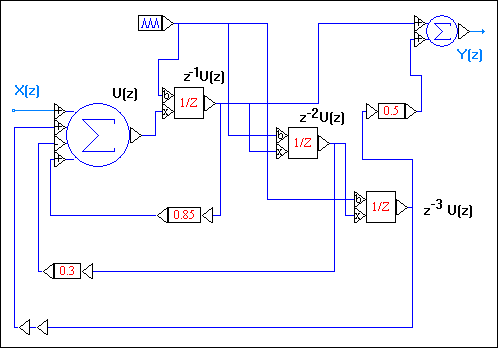
Slika 3.4.30. Simulacijski prikaz zadane impulsne prijenosne funkcije

Simulacijska izvedba zadane impulsne prijenosne funkcije prikazana je na slici 3.4.30, gdje je korišten programski paket VisSim. Impulsna prijenosna funkcija se može u cijelosti i sklopovski izvesti na temelju istog prikaza. Potrebno je samo sklopovski izgraditi pojedinačne elemente, zbrajala, sklopove za kašnjenje i množila s konstantom i na kraju ih sve povezati na izvedeni način.

Kod primjene programskog paketa VisSim vidi se da sklopovi za kašnjenje imaju dva ulaza. Jedan pripada signalu kojeg treba zakasniti, a drugi generatoru uzorkovanja, kojem se u simulacijskim programima može mijenjati T (Time Between Pulses) , prema slici 3.4.31.

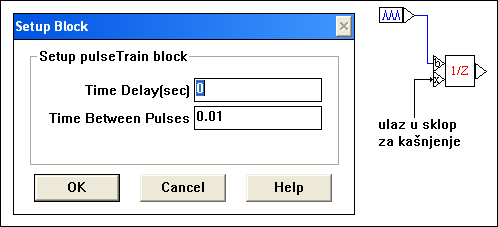
Slika 3.4.31. Uzorkovanje s izabranim T = 0.01 s

4. Odziv sustava na pobudu zadanu nasumičnim nizom uzoraka i na temelju poznate impulsne prijenosne funkcije – Diskretna konvolucija

Diskretni sustav opisan je impulsnom prijenosnom funkcijom G(z). Ulazni je signal zadan nizom uzoraka za koje se ne može odrediti zajednički funkcionalni oblik i ne može se prikazati Z – transformacija. Odrediti vrijednosti tri uzorka odziva.

Poznata je impulsna prijenosna funkcija:

Poznati su i uzorci ulaznog signala: x(0) = 1; x(T) = 0.85; x(2T) = 0.726.

U slučajevima kad je ulazni signal prepoznat samo nizom uzoraka ili je čak impulsna prijenosna funkcija identificirana samo nizom uzoraka (tada uzorci impulsne prijenosne funkcije predstavljaju karakteristični odziv na diskretnu Diracovu funkciju), odziv sustava se određuje diskretnom konvolucijom.

Svaki uzorak odziva može se izračunati pomoću relacije:

Uzorci ulaznog signala su zadani. Potrebno je impulsnu prijenosnu funkciju izraziti uzorcima, a to se opet postiže inverznom Z – transformacijom ili:

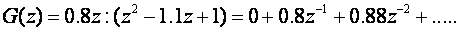
g(0) = 0; g(T) = 0.8; g(2T) = 0.88

Primijenimo li oblik izraza za diskretnu konvoluciju koji povezuje uzorke g(nT - kT) i x(kT), vrijedi:

Identičan se rezultat dobije primjenom drugog oblika za diskretnu konvoluciju koji povezuje uzorke x(nT – kT) i g(kT).