3.5. Opis diskretnog sustava varijablama stanja
Opis ponašanja dinamičkog sustava temeljen na prijenosnoj funkciji temelji se na ulazno – izlaznim vrijednostima, što drugim riječima znači na ponašanju sustava kakvim se on pokazuje prema vani, a cjelokupna se analiza i sinteza više manje provodi u s području kod kontinuiranih, odnosno u z području kod diskretnih sustava. Tek se konačni izraz ponovo vraća u vremensko područje, s obzirom da mi živimo u vremenskom području te nas prvenstveno zanima kakvo će biti ponašanje sustava u ovisnosti o vremenu. Kao alternativa ovakvom načinu opisa ponašanja sustava postoji i postupak kod kojega se većina analiza provodi u vremenskom području, nema potrebe prelaska u neko drugo područje, pa tek na kraju vraćanje rezultata u vremensko. Postupak se temelji na uvidu u unutrašnje ponašanje sustava uvodeći pojam stanja, odnosno varijabli stanja sustava. Uobičajeno je da se postupci temeljeni na prijenosnoj funkciji obično nazivaju klasični postupci (eng. Classical Design Techniques), a postupci temeljeni na varijablama stanja moderni postupci (eng. Modern Design Techniques) projektiranja regulacijskog sustava.
Varijable stanja definiramo kao minimalni broj unutrašnjih varijabli sustava kojima možemo u potpunosti opisati ponašanje sustava. Ima ih onoliko koliko sustav ima komponenata sa sposobnošću pohrane energije, što znači da broj varijabli stanja odgovara redu prijenosne funkcije. Opis sustava jednadžbama varijabli stanja sastoji se u tome da se ponašanje dinamičkog sustava umjesto diferencijalnom jednadžbom n-tog reda, prikaže sustavom od n diferencijalnih jednadžbi prvog reda u kanoničkoj formi:
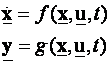(3.5.1)
gdje je x vektor varijabli stanja, u vektor ulaznih veličina, y vektor izlaznih veličina, a t nezavisna varijabla – vrijeme.
Ukoliko varijable stanja odgovaraju fizičkim, mjerljivim veličinama sustava nazivamo ih fizičke varijable stanja.
Gledano s praktičke strane, često je zgodnije varijable stanja definirati derivacijama izlazne veličine
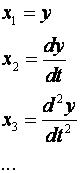(3.5.2)
Ovako definirane varijable stanja nazivamo faznim varijablama stanja. Fazne varijable stanja mogu biti i fizičke varijable stanja.
Tipičan primjer kod kojega se fazne i fizičke varijable stanja poklapaju je istosmjerni motor upravljan strujom magnetiziranja kod kojeg je izlazna veličina kutni pomak. Motor se (uz zanemarivanje trenja i induktiviteta namota) opisuje diferencijalnom jednadžbom drugog reda što znači da njegovo ponašanje možemo opisati s dvije varijable stanja. Fazne varijable stanja bi bile: izlazni kutni pomak i njegova derivacija - kutna brzina. To su ujedno i fizičke varijable stanja s obzirom da se i kutni pomak i kutna brzina mogu mjeriti. Drugi primjer fizičkih varijabli stanja, koje nisu i fazne je izbor struje magnetiziranja i kutnog pomaka za varijable stanja.
Kod diskretnih sustava fazne varijable stanja se definiraju izlaznom veličinom y(kT) i njenim diskretnim pomacima y[(k+1)T], y[(k+2)T] itd.
Jednadžbe varijabli stanja linearnih vremenski nepromjenjivih sustave (eng. LTI System – Linear Time – Invariant System) opisujemo matričnim jednadžbama:
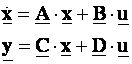(3.5.3)
Prva se jednadžba naziva jednadžba varijabli stanja (eng. State Equation), a druga jednadžba izlaza (eng. Output Equation). A , B , C i D su matrice koeficijenata, od kojih se matrica A naziva matrica stanja sustava.
Prebacimo se sada na diskretne sustave. I njih možemo opisati jednadžbama varijabli stanja s tim da diferencijalna jednadžba postaje jednadžba diferencija prvog reda. Za linearne diskretne, vremenski nepromjenjive sustave jednadžbe glase
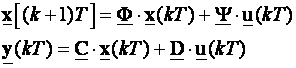(3.5.4)
a Φ , Ψ , C i D su također matrice koeficijenata. Grafički prikaz jednadžbe (3.5.3) dan je na slici 3.5.1.
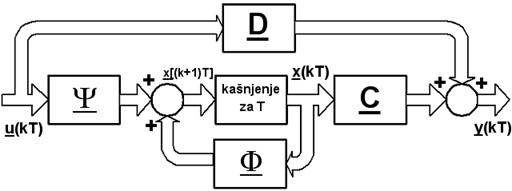
Slika 3.5.1. Diskretni sustava opisan jednadžbama varijabli stanja
Primjer:
Sustav opisan jednadžbom diferencija trećeg reda prebacite u opis varijablama stanja.
Sustav je trećeg reda pa trebamo definirati tri varijable stanja. Fazne varijable stanja su:
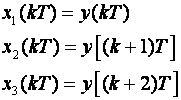
pa jednadžbe varijabli stanja glase:
