3.5.1. Određivanje jednadžbi stanja diskretnog sustava iz poznatih jednadžbi stanja kontinuiranog sustava
Zadatak nam je za poznate matrice A , B , C i D odrediti nepoznate matrice Φ , Ψ , C i D . Ispred kontinuiranog dijela sustava nalazi se sklop za obnavljanje tako da se u stvari radi o određivanju diskretnog modela varijabli stanja ekvivalentnog sustava. Opće rješenje jednadžbe (3.5.3) u trenutku t je:
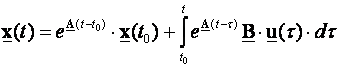(3.5.5)
Prvi dio je slobodni odziv pod utjecajem početnog stanja sustava, a drugi prinudni odziv, pod utjecajem vanjske pobude koja je između dva perioda uzorkovanja konstantna s obzirom da se ispred kontinuiranog sustava nalazi sklop za obnavljanje 0-tog reda. Pređimo sada u diskretno područje na način da nas zanima što se događa između dva slijedeća perioda uzorkovanja. Zbog toga uvodimo zamjenu t0=kT i t=(k+1)T :
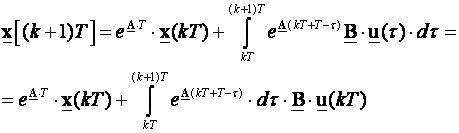(3.5.6)
Napomena: u(τ) smo izvadili izvan integrala budući da se on ne mijenja između kT i (k+1)T s obzirom da je ispred sustava sklop za obnavljanje 0-tog reda. Vrijednost mu je stalno ista i jednaka vrijednosti na početku intervala pa ga zato i izvlačimo kao u(kT).
Uvedemo li novu zamjenu τ=T+kT-μ te u skladu s njom promijenimo i granice integracije dobijemo:
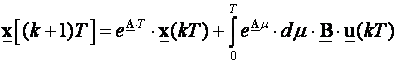
Usporedimo li jednadžbu (3.5.7) i prvi dio jednadžbe (3.5.4) očito je da vrijedi
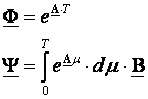(3.5.8)
Riješimo se najprije integrala. Kako su A i B matrice konstanti vrijedi
(3.5.9)
Prikažimo sada
beskonačnim redom
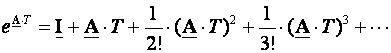(3.5.10)
te uvrstimo u izraze za proračun matrica stanja diskretiziranog sustava
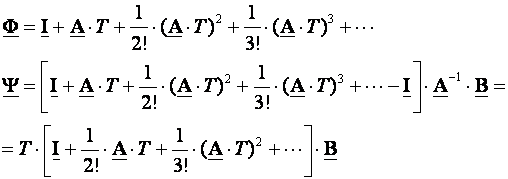(3.5.11)
U nekim specijalnim situacijama jednadžbu (3.5.11) možemo i aproksimirati. Na primjer ukoliko je period uzorkovanja jako mali možemo uzeti samo prve članove reda
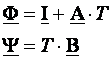(3.5.12)
ili ukoliko nije toliko mali možemo uzeti samo nekoliko članova reda. Amerikanac H.M. Paynter (H.M. Paynter, "Analysis and Design of Engineering Systems", MIT Press, 1961) daje naputak za određivanje broja potrebnih članova reda. Sastoji se iz tri koraka:
1. Odredi q=max|aij.T| gdje su aij elementi matrice A.
2. Proračunaj konstantu p tako da zadovoljava empirijsku jednadžbu
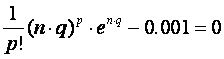(3.5.13)
gdje je n red sustava (dimenzija matrice A).
3. Izračunaj Φ i Ψ do p-tog člana reda.
Jednadžba
(3.5.13) rješava se metodom pokušaja. Pogledajmo primjer za
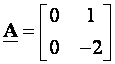i T=0.1. Za ove vrijednosti matrice q=0.2 i n=2. Lijevi
dio jednadžbe (3.5.13) za različite vrijednosti konstante p daje sljedeće
rezultate:
p=1 , rezultat na lijevoj strani = 6.391
p=2 , rezultat na lijevoj strani = 4.782
p=3 , rezultat na lijevoj strani = 2.767
p=4 , rezultat na lijevoj strani = 0.4645
p=5 , rezultat na lijevoj strani = -2.061
Rezultat najbliži nuli je za p=4, pa se kod proračuna trebaju uzeti 4 člana reda.
Napomena: Kako bismo pokazali da se pri rješavanju ove jednadžbe može koristiti i simulacijski program VisSim, napisan je mali program na način da je jednadžba (3.5.13) logaritmirana:
(3.5.14)
Program je polu-interaktivan, što znači da je za svaku postavljenu vrijednost p potrebno rekonfigurirati množilo koji računa p! (dodati ili oduzeti faktore). Slika 3.5.2 pokazuje situaciju za p=4.
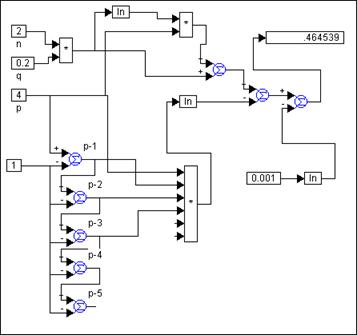
Slika 3.5.2. Rješavanje jednadžbe za empirijski proračun broja
članova reda kod određivanja matrica jednadžbi varijabli stanja diskretnog
sustava za p=4
(paynter_algorithm.vsm)
Marice Φ i Ψ je teško računati bez dobre programske podrške. Matlab ima već gotove funkcije za njihov proračun.
Sljedeći zadatak je kako riješiti
jednadžbe varijabli stanja diskretnog sustava.