3.5.2. Rješavanje jednadžbi stanja diskretnog sustava iteracijskim postupkom
Zadatak nam je riješiti jednadžbu:
(3.5.15)
Najjednostavniji postupak je rekurzivni iteracijski postupak. Krene se od k=0, pa se dobiveni rezultat koristi u rješenju za k=1 itd.
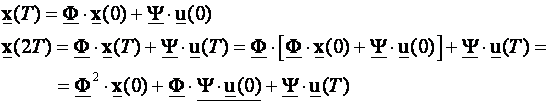(3.5.16)
I tako redom do trenutka kT:
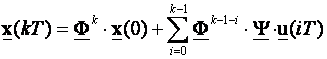(3.5.17)
Jednadžba (3.5.17) je rješenje jednadžbe varijabli stanja koje se nakon toga može uvrstiti u jednadžbu izlaza.
Primjer:
Riješi sustav opisan jednadžbama varijabli stanja:
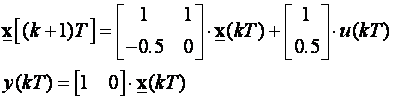
za nulte početne uvjete i jediničnu odskočnu funkciju na ulazu.
Računamo korak po korak:
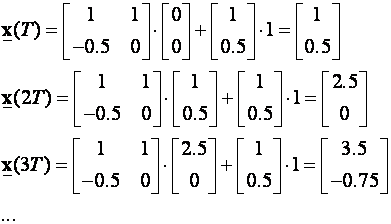
Do istog se rezultata jednostavno dolazi i u VisSimu koristeći blok za opis sustava varijablama stanja:
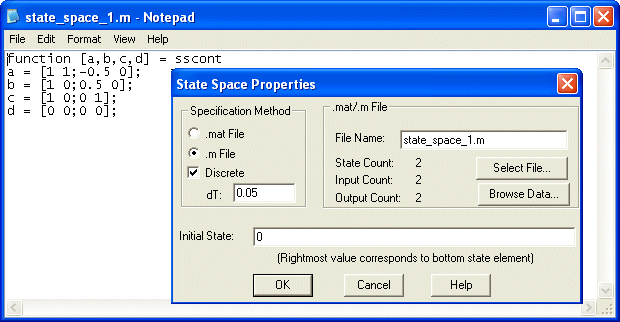
Slika 3.5.3. Način definiranja diskretnog sustava varijablama stanja u VisSimu
Vidi se da se radi o diskretnom sustavu s periodom uzorkovanja 0.05 sekundi. Kako bi mogli crtati obje varijable stanja definiraju se dva izlaza i svakoj izlaznoj varijabli se pridruži jedna od varijabli stanja (vidi matricu C). Zbog toga se morao uvesti i drugi ulaz bez utjecaja na varijable stanja (vidi matricu B koja odgovara matrici Ψ ). Matrica A odgovara matrici Φ.
Slika 3.5.4 prikazuje dobiveno rješenje. Lako je uočiti da se prva tri trenutka podudaraju s prije izračunatim vrijednostima.
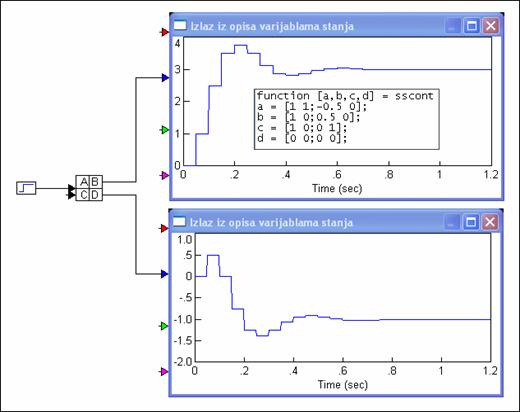
Slika 3.5.4. Rješenje jednadžbi varijabli stanja diskretnog
sustava za T=0.05
(varijable_stanja_rjesavanje.vsm)