4.1. Stabilnost diskretnih sustava
Pretpostavljamo da je čitatelju poznat pojam stabilnosti kontinuiranih sustava. Postoji više različitih matematičkih definicija stabilnosti. Ovdje ćemo razmatrati samo dvije od njih i to: asimptotsku stabilnost i tkz. BIBO stabilnost koja dolazi od engleskog izraza Bounded Input Bounded Output što bi se moglo prevesti kao stabilnost ograničenog odziva na ograničenu pobudu (OOOP stabilnost). Asimptotska stabilnost odnosi se na sustav bez vanjske pobude, a BIBO stabilnost na sustav s vanjskom pobudom. Počnimo s formalnim definicijama:
Asimptotska stabilnost
Linearni, vremenski nepromjenjivi sustav (LTI – eng. Linear Time Invariant) je asimptotski stabilan onda i samo onda kada odziv bez prisustva vanjske pobude teži nuli kada vrijeme teži u beskonačno. Ako je x(kT) vektor varijabli stanja sustava, a u(kT) vektor ulazne pobude, asimptotsku stabilnost matematički definiramo izrazom:
(4.1.1)
što povlači da i izlazi sustava y(kT) trebaju težiti 0.
BIBO stabilnost
Linearni, vremenski nepromjenjivi sustav (LTI – eng. Linear Time Invariant) je BIBO stabilan onda i samo onda kada ograničena pobuda daje ograničeni odziv za bilo kakve početne uvjete. Matematički to pišemo:
(4.1.2)
što isto tako povlači da će i izlazi sustava biti ograničeni.
Ovo su općenite definicije. Puno praktičnija definicija asimptotske stabilnost je vezana s korijenima karakteristične jednadžbe, a kako su korijeni karakteristične jednadžbe polovi impulsne prijenosne funkcije, definicija je vezana s položajem svih polova impulsne prijenosne funkcije u z ravnini.
Neka je G(z) impulsna prijenosna funkcija a g(kT) njena inverzna Z - transformacija.
Napomena: g(kT) je impulsni odziv sustava – odziv sustava na Diracovu impulsnu pobudu.
Sustav je asimptotski stabilan ukoliko su svi polovi impulsne prijenosne funkcije G(z) unutar jediničnog kruga z ravnine.
Dokaz je direktan i na neki smo ga način već pokazali u poglavlju 3.4.5. Na temelju jednadžbe (3.4.89) odziv sustava u z području je
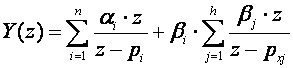(4.1.3)
gdje su pi polovi impulsne prijenosne funkcije ekvivalentnog sustava GE(z), a pxj polovi Z - transformacije ulaznog signala.
Prebacimo li jednadžbu u vremensko područje možemo pisati
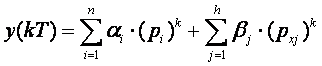(4.1.4)
Napomena: Radi jednostavnosti pisanja izostavili smo množenje desne strane jednadžbe sa skokovitim signalom koji nam osigurava da je za negativne k izlazni signal jednak 0.
Asimptotska stabilnost se definira za sustav bez ulazne pobude (slobodni odziv), pa je za nju važna samo prva suma:
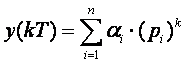(4.1.5)
Odziv sustava će težiti nuli kada k teži u beskonačno onda i samo onda ako za sve polove vrijedi nejednakost | pi |< 1 što znači da svi polovi trebaju biti unutar jedinične kružnice. U tom je slučaju
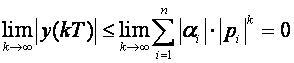(4.1.6)
Do istog se rezultata dolazi analizom preslikavanja s ravnine u z ravninu o čemu govorimo u poglavlju o analizi slobodnog odziva diskretnog sustava.
Nužan uvjet BIBO stabilnosti je
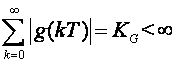(4.1.7)
gdje je g(kT) impulsni odziv sustava (karakteristični odziv) u z domeni definiran izrazom
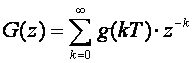(4.1.8)
Napišimo izraz za izlaz sustava u obliku konvolucijske sume (jednadžba slična jednadžbi (3.4.14) u kojoj smo t zamijenili sa kT i ulaz sustava definirali kao u(t)):
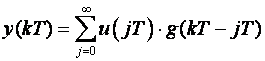(4.1.9)
Kako su g(t) = 0 i u(t) = 0 za t < 0 izraz (4.1.9) možemo pisati i u obliku
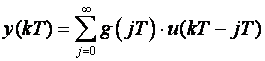(4.1.10)
Ukoliko je pobuda ograničena (vidi(4.1.2)) i ispunjen uvjet (4.1.7) vrijedi
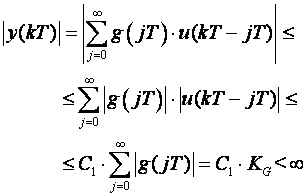(4.1.9)
iz čega slijedi da je i odziv ograničen, što znači da je sustav BIBO stabilan.
Asimptotska stabilnost je stroži uvjet i ona uključuje BIBO stabilnost, a BIBO stabilnost uključuje asimptotsku stabilnost samo ukoliko je sustav upravljiv i osmotriv. Može se dogoditi da se korijeni karakteristične jednadžbe koji su izvan jedinične kružnice ponište nulama, pa bi sustav bio BIBO stabilan, ali ne bi bio asimptotski stabilan zato što ona zahtijeva da svi korijeni karakteristične jednadžbe uključivo i ove poništene budu unutar jedinične kružnice.