4.1.1. Test stabilnosti
Stabilnost testiramo na način da provjeravamo polove impulsne prijenosne funkcije sustava. Ukoliko su svi unutar jedinične kružnice sustav je stabilan. Stabilnost provjeravamo kriterijima stabilnosti. Kod kontinuiranih sustava to su Hurwitzov i Routhov kriterij, a kod diskretnih sustava najčešće se koristi Jurryev test stabilnosti.
Neka je
![]() (4.1.9)
(4.1.9)
nazivnik impulsne prijenosne funkcije sustava čiju stabilnost testiramo.
Sustav je stabilan ukoliko su zadovoljeni sljedeći uvjeti:
1. Za z = 1, P(z) je pozitivan: P(z)|z=1>0
2. Za z = -1 produkt (-1)n.P(z) je pozitivan : (-1)n.P(z)|z=1>0
3. Formiramo Jurryevu tablicu:
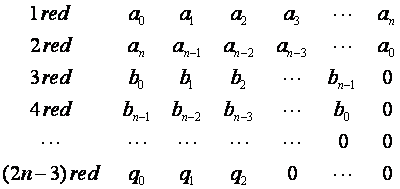
gdje se elementi 3. i 4. reda računaju pomoću formule
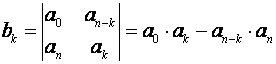
elementi 5. i 6. reda formulom
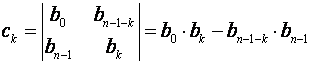
elementi 7. i 8. reda formulom
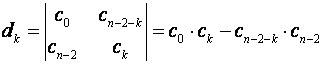
sve do (2n-3) reda koji ima samo tri člana

Sustav je stabilan ukoliko vrijedi
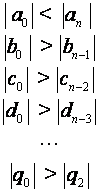
Primijenimo Jurryev test na sustave drugog i trećeg reda.
Sustav drugog reda
![]()
Napomena: Jednadžbu smo napisali u obliku koji ima jedinicu uz najveću potenciju varijable z. Do tog oblika dolazimo ako jednadžbu podijelimo s koeficijentom uz najveću potenciju varijable z.
Sustav je stabilan ukoliko zadovoljava sljedeće uvjete:
1.
![]()
2.
![]()
3.
![]()
Uvjete 1. i 2. možemo prebaciti u oblik
![]()
![]()
pa slika 4.1.1 pokazuje stabilno područje unutar kojega trebaju biti koeficijenti sustava drugog reda
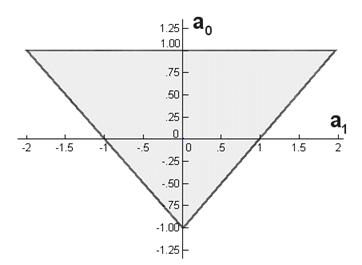
Slika 4.1.1. Stabilno područje koeficijenata sustava drugog reda
Sustav trećeg reda
![]()
1.
![]()
2.
![]()
Formiramo Jurryevu tablicu
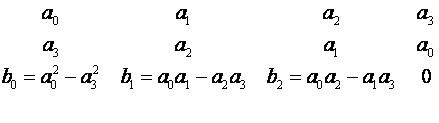
pa je treći uvjet
3. a)
![]()
b)
![]()
Primjer:
![]()
![]()
1.
![]()
2.
![]()
3. a)
![]()
b)
![]()
pa je zaključak da svi polovi jednadžbe P(z) leže unutar jedinične kružnice. Riješimo li jednadžbu dobiti ćemo
![]()
pa vidimo da su svi polovi realni i manji od jedinice.
Na kraju pogledajmo kako se Jurryev test stabilnosti koristi kod analize stabilnosti regulacijskog sustava s negativnom povratnom vezom. Uzet ćemo primjer sa slike 3.2.4.
Primjer:
Regulacijski je sustav prikazan slikom 4.1.2.
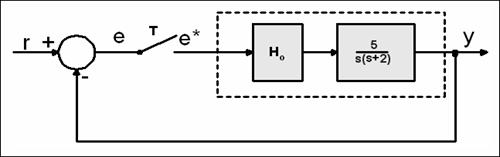
Slika 4.1.2. Diskretni regulacijski sustav za koji analiziramo uvjete stabilnosti
GE(z) smo već prije izračunali
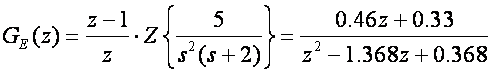
Impulsna prijenosna funkcija zatvorenog regulacijskog sustava glasi
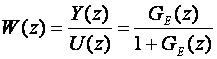
pa je nazivnik impulsne prijenosne funkcije zatvorenog sustava (karakteristični polinom) jednak
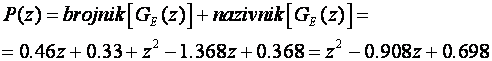
iz čega slijedi
![]()
Provjeravamo kriterije stabilnosti
1.
![]()
2.
![]()
3.
![]()
iz čega slijedi da je sustav stabilan. Izračunamo li polove zatvorenog regulacijskog sustava dobiti ćemo
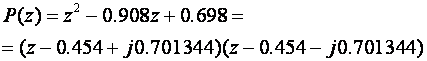
pa vidimo da su polovi konjugirano kompleksni i unutar jedinične kružnice.
Svi signali sustava uz skokovitu pobudu prikazani su na slici 4.1.3. Sustav ima prigušeni oscilatorni odziv s obzirom da su mu polovi konjugirano kompleksni.
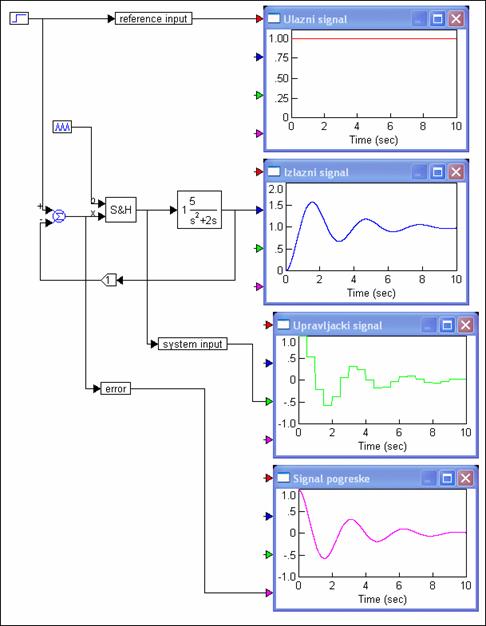
Slika 4.1.3. Simulacija odziva sustava sa slike 4.1.2 za T=0.5
(vremenski_odziv_2.vsm)