3.4.2.1. Razvoj na parcijalne razlomke i korištenje tablica
Funkcija W(s) se razvije na parcijalne razlomke standardnih tabličnih oblika, proračunaju se koeficijenti i direktno se pređe u z područje. Znači standardna primjena tablica Z - transformacije kao i kod pretvaranja X(s) u X(z) o čemu smo govorili u poglavlju 3.3. Pogledajmo primjer:
Primjer:
Proračunaj W(z) ako je poznat W(s) !
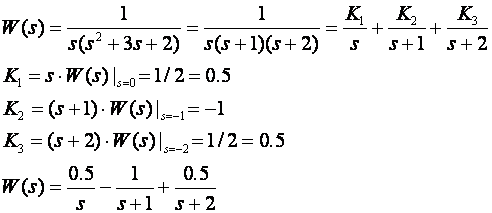
Tablice na slici 3.3.1 daju
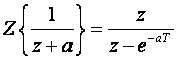
pa dobijemo
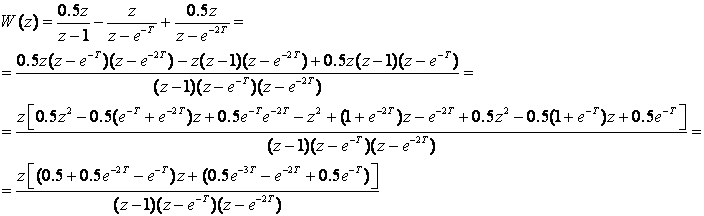
Ponovimo još jedan put Z - transformacije nekih tipičnih oblika funkcija W(s) zadanih u s području.
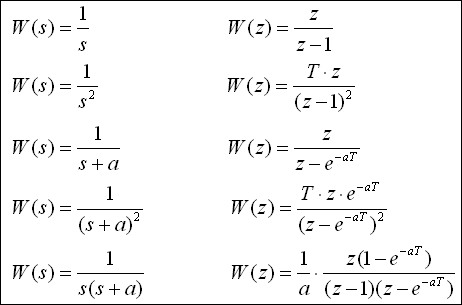
Slika 3.4.5. Z - transformacija tipičnih oblika funkcije W(s)
S praktične strane gledanja najčešći nam je zadatak prebaciti prijenosnu funkciju kontinuiranog sustava kojeg namjeravamo voditi u z područje. U prethodnom smo poglavlju pokazali da se ispred njega uvijek nalazi sklop za obnavljanje i to najčešće 0-og reda, pa nas u praksi zanima Z - transformacija njihovog serijskog spoja, odnosno Z – transformacija ekvivalentnog sustava (jednadžba (3.4.21)). Zbog toga bi nam bilo puno korisnije navesti tablicu u kojoj je izračunat
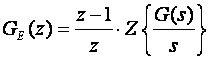
za neke osnovne oblike prijenosne funkcije samog sustava G(s). Tablica je dana na slici 3.4.6 (Pazite polazni oblik u tablici iz kojeg se računa GE(z) je G(s), a ne G(s)/s !). GE(z) je definiran kao razlomljeni racionalni razlomak oblika:
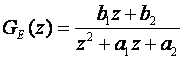

Slika 3.4.6. Impulsna prijenosna funkcija ekvivalentnog sustava za tipične oblike prijenosne funkcije G(s)
Pogledajmo još jedan put prethodni primjer sada malo modificiran:
Primjer:
U prethodnom primjeru bio nam je zadan W(s)
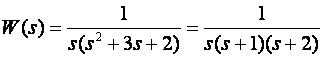
Pretpostavimo li da je W(s) kvocijent W(s)=G(s)/s, prijenosna funkcija čiju impulsnu prijenosnu funkciju ekvivalentnog sustava tražimo bit će
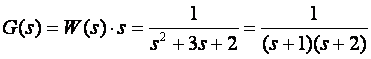
Iz tablice na slici 3.4.6 slijedi
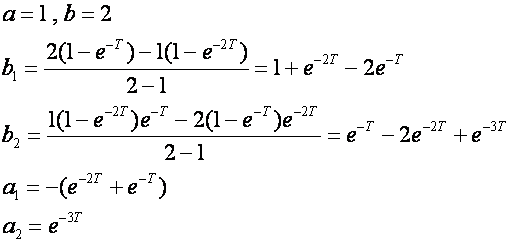
pa je
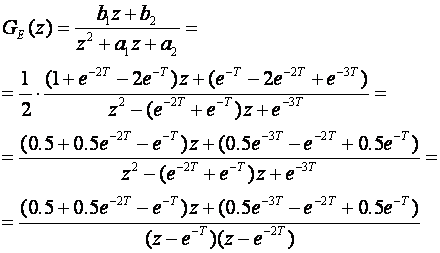
Usporedimo GE(z) i W(z) iz prethodnog primjera. Odmah se vidi da je
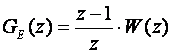
pa je
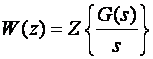
što smo i pretpostavili na početku ovog primjera.
Usporedimo na kraju odziv sustava GE(z) i sustava G(z) koji je dobiven Z - transformacijom samo kontinuiranog dijela prijenosne funkcije G(s) (nju dobijemo tako da GE(s) pomnožimo sa s):
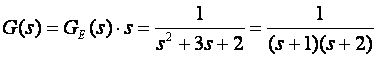
Računamo najprije G(z)
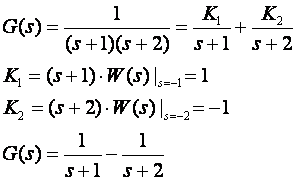
Tablice na slici 3.3.1 daju
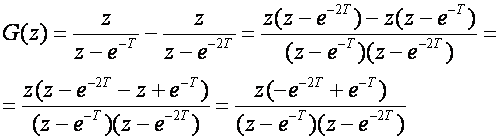
Za T=0.1 imamo
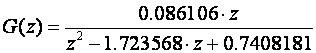
Slika 3.4.7 prikazuje odziv kontinuiranog sustava, ovako dobivenog diskretnog sustava i diskretnog sustava dobivenog prebacivanjem GE(s) u z područje.
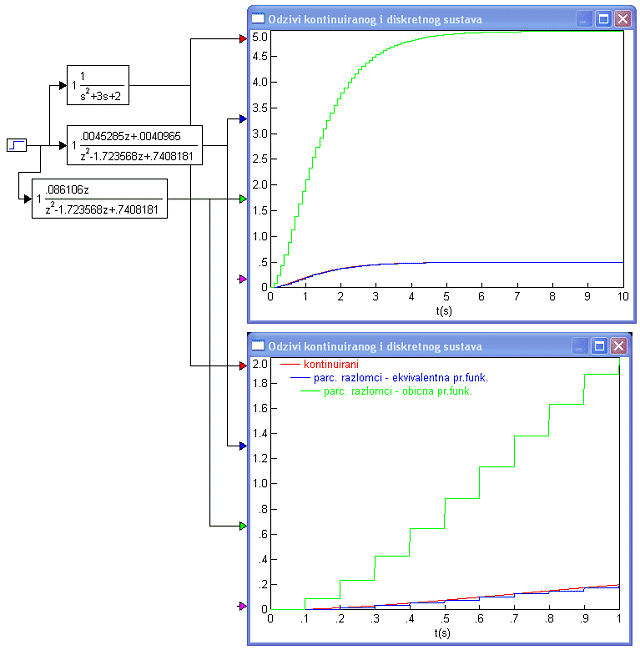
Slika 3.4.7. Odzivi kontinuiranog sustava i diskretnog sustava čija je impulsna prijenosna funkcija dobivena razvojem na parcijalne razlomke ekvivalentne prijenosne funkcije GE(s) i razvojem na parcijalne razlomke obične prijenosne funkcije G(s) za T=0.1 (Diskretizacija_ekvivalentna_i_obicna_tablica.vsm)
Razlika je u tome što odziv
diskretnog sustava kod kojeg smo prebacili samo prijenosnu funkciju G(s) u z
područje u stacionarnom stanju teži vrijednosti 5 koja je 10 puta veća od vrijednosti
kojoj teže odzivi kontinuiranog sustava i
diskretnog sustava temeljenog na ekvivalentnoj prijenosnoj funkciji.
Promijenimo li T na 0.5 odziv sustava temeljenog na diskretizaciji prijenosne
funkcije G(s) teži novoj vrijednosti koja sada iznosi 10, a za T=0.05
vrijednosti 0.96, dok odzivi diskretnog sustava temeljenog na ekvivalentnoj
prijenosnoj funkciji i dalje teže istoj vrijednosti 0.5, kojoj teži i
kontinuirani sustav.
Razlog ovoj pojavi smo već spominjali uz sliku 3.4.1 i 3.4.2. Prebacivanje samo prijenosne funkcije u z područje odgovara situaciji kada na ulaz kontinuiranog sustava dovedimo diskretni signal. U tom slučaju period uzorkovanja djeluje kao obrnuto proporcionalno “konstantno pojačanje”. Što je period veći, pojačanje je manje (vidi komentar i sliku 3.4.1). Kod diskretizacije temeljene na ekvivalentnoj prijenosnoj funkciji sustav se ponaša kao da je na njegov ulaz doveden signal propušten kroz sklop za obnavljanje 0-tog reda, pa razlike u amplitudi više nema (vidi komentar i sliku 3.4.2).
Metoda koja se u praksi dosta koristi
je aproksimacijska metoda kod koje se u W(s) napravi zamjena svakog s
funkcijom od z. Sljedeće poglavlje detaljno obrađuje ovaj postupak.