3.4.1. Ekvivalentni sustav
Počnimo s primjerom. Neka je kontinuirani sustav opisan prijenosnom funkcijom
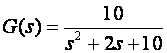
Dovedimo na njegov ulaz diskretiziran sinusni signal jedinične amplitude i frekvencije 1Hz (6.3 rad/sek) x(t)=sin(6.3t) za period uzorkovanja T = 0.1 sekundu i T = 0.02 sekunde. Rezultat prikazuje slika 3.4.1.
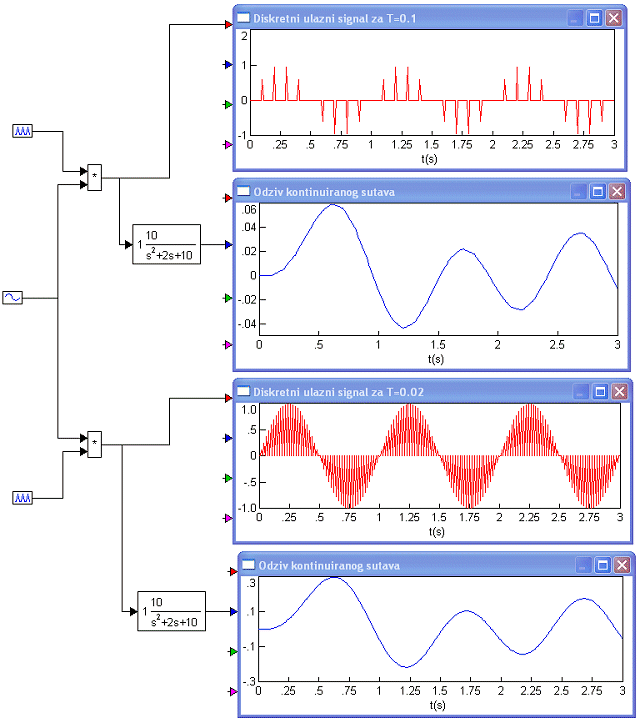
Slika 3.4.1 Odziv kontinuiranog sustava na diskretni signal
Lako je uočiti da su amplitude odziva sustava za različite periode uzorkovanja bitno različite. Razlog je taj što energija prenesena sustavu ovisi o tome koliko impulsa dođe na ulaz sustava. Period uzorkovanja djeluje kao obrnuto proporcionalno “konstantno pojačanje”. Što je period uzorkovanja veći, to je prividno pojačanje manje. Situacija je bitno drugačija ukoliko se diskretni signal prije dovođenja na ulaz kontinuiranog sustava propusti kroz sklop za obnavljanje 0-tog reda (slika 3.4.2).
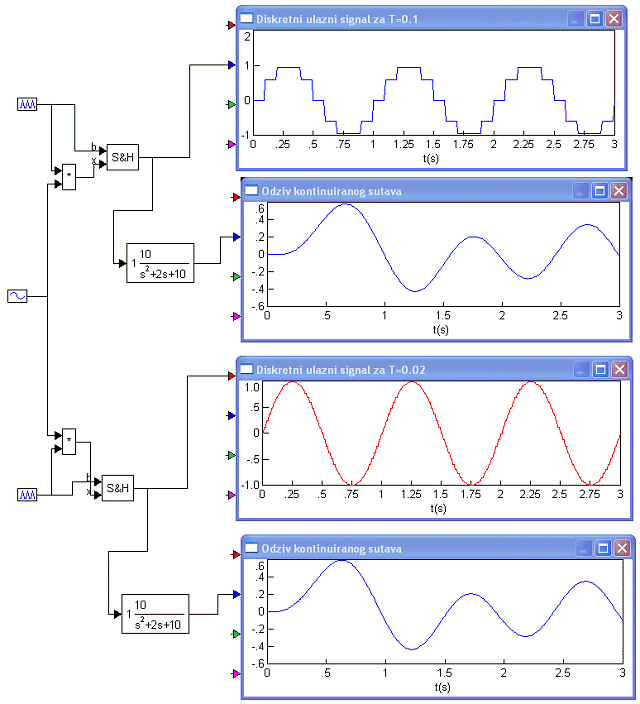
Slika 3.4.2. Odziv kontinuiranog sustava na diskretni signal propušten kroz sklop za obnavljanje 0-tog reda
Za oba perioda uzorkovanja razlika u odzivu ne može se uočiti.
Upravo zbog toga diskretni signal se nikada direktno ne dovodi na kontinuirani sustav. Uvijek se najprije propusti kroz sklop za obnavljanje 0-tog reda, što znači da se u svim primjenama sklop za obnavljanje uvijek nalazi ispred kontinuiranog sustava koji se vodi. Takav serijski spoj sklopa za obnavljanje 0-tog reda i kontinuiranog sustava G(s) nazivamo ekvivalentni sustav. U kontinuiranom području njegovu prijenosnu funkciju označavamo GE (s), a u diskretnom području GE (z). Pogledajmo kako se proračunava GE (z) ukoliko je poznata prijenosna funkcija kontinuiranog sustava G(s).
Ekvivalentni sustav se blokovski prikazuje na slici 3.4.3.
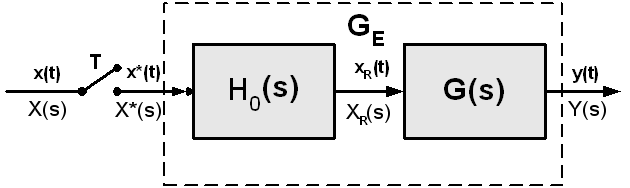
Slika 3.4.3. Blokovski prikaz ekvivalentnog sustava kao serijski spoj sklopa za obnavljanje 0-tog reda i kontinuiranog sustava
Pogledajmo što se događa u Laplaceovom području
(3.4.8)
Kako je X*(s) Laplaceova transformacija diskretnog signala
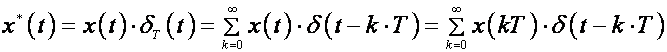
možemo pisati
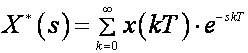
Prijenosna funkcija sklopa za obnavljanje 0-tog reda je prema (2.3.7)
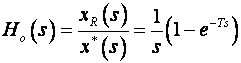(3.4.9)
pa je
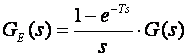(3.4.10)
Izlaz sustava je
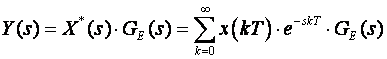(3.4.11)
što u vremenskoj domeni daje
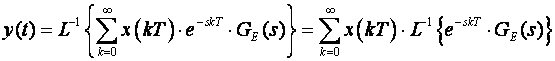(3.4.12)
Teorem pomaka Laplaceove transformacije
(3.4.13)
daje odziv ekvivalentnog sustava u vremenskom području
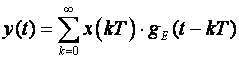(3.4.14)
gdje je gE(t) inverzna Laplaceova transformacija funkcije GE(s).
Zanimljivo je pogledati što će se dogoditi ako se uzorkuje i izlazni signal y(t)?
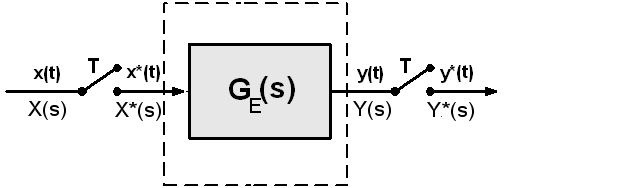
Slika 3.4.4. Blokovski prikaz ekvivalentnog sustava kod kojeg se uzorkuje i izlazna veličina y(t)
Pišemo
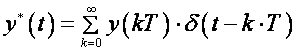(3.4.15)
gdje prema (3.4.14) uz zamjenu t=kT i promjenu indeksa sumacije k u j, y(kT) postaje konvolucijska suma:
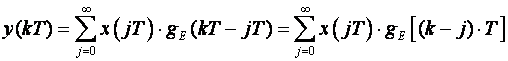
Napomena: U biti zbrajanje treba ići samo do člana k:
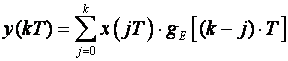
zato što je za negativne diskretne trenutke vremena gE jednak nuli pa ga nije nužno ni pisati. Međutim kako nam u kasnijim manipulacijama sumama odgovara da sumiranje ide do beskonačno u nastavku ćemo zadržati oblik (3.4.16).
U Z domeni jednadžba (3.4.15) postaje:
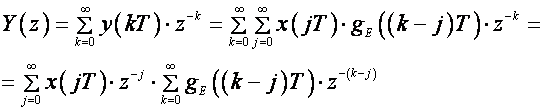(3.4.17)
kako je gE(t) = 0 za t < 0, u drugoj sumi se može napraviti zamjena n=k – j pa iz jednadžbe (3.4.17) dobijemo:
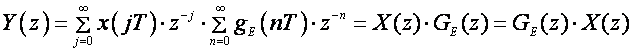(3.4.18)
Jedino što nam sada treba da bismo analogni dio sustava prebacili u diskretni svijet je Z - transformacija od gE(t). Pregrupirajmo jednadžbu (3.4.10) u oblik:
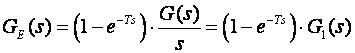(3.4.19)
Neka je g1(t) karakterističan odziv od G1(s). Koristeći teorem pomaka Laplaceove transformacije (3.4.19) u vremenskom području možemo napisati
(3.4.20)
Prebacimo li (3.4.20) u z područje korištenjem teorema pomaka Z - transformacije dobijemo
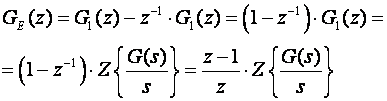(3.4.21)
Dakle GE(z) dobijemo tako da Z - transformaciju kvocijenta G(s)/s pomnožimo sa članom (1-z-1). U engleskoj literature formula (3.4.21) se ponekad naziva “Staicase Input Formula” .