5.2.2. Postupak temeljen na postavljanju polova (i nula) regulatora i definiranju željenog modela vođenog sustava
Postupak se u engleskom govornom području zove Pole-Placement Using Output Feedback and Polynomial Design pa bi ga mogli i nazvati postupak postavljanja polova regulatora temeljen na povratnoj vezi po izlazu i projektu polinoma.
Osnovni ideja je jednostavna i sastoji se od tri glavna dijela:
a) prikazati kontinuirani dio sustava odgovarajućom impulsnom prijenosnom funkcijom,
b) definirati željenu impulsnu prijenosnu funkciju zatvorenog regulacijskog sustava,
c) proračunati regulator tako da se odziv vođenog zatvorenog regulacijskog sustava poklapa sa željenom impulsnom prijenosnom funkcijom zatvorenog sustava.
Pri tome je potrebno voditi računa o nekoliko bitnih stvari:
Diskretni ekvivalent vođenog sustava treba što vjernije oponašati kontinuirani sustav. U poglavlju 3.4.2 Dobivanje impulsne prijenosne funkcije W(z) iz W(s) detaljno smo analizirali postupke iznalaženja takve, odgovarajuće impulsne prijenosne funkcije iz poznate prijenosne funkcije sustava u kontinuiranom području. U obzir dolazi proračun impulsne prijenosne funkcije ekvivalentnog sustava korištenjem tablica, aproksimacijski postupci ili postupak temeljen na metodi poklapanja polova i nula. Bez obzira kako je proračunat diskretni oblik prijenosne funkcije kontinuiranog sustava on je razlomljena racionalna funkcija varijable z:
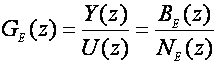(5.2.3)
Namjerno smo stavili indeks E kako bismo naglasili da treba biti ekvivalentni sustav (serijski spoj sklopa za obnavljanje i kontinuiranog sustava) ili njemu odgovarajući oblik dobiven drugim postupcima.
Željeno ponašanje zatvorenog sustava vođenja definiramo njegovom željenom impulsnom prijenosnom funkcijom koja je također razlomljena racionalna funkcija varijable z:
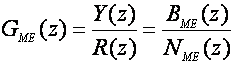(5.2.4)
Do ove funkcije možemo doći direktnim definiranjem njenih polova i nula u z ravnini kojima osiguravamo određeno ponašanje sustava, međutim kako se na kraju mi ipak trebamo vratiti u kontinuirano područje, s obzirom da je sustav koji se vodi kontinuiran prirodniji je način definiranja željene prijenosne funkcije vođenog sustava u s području GM(s) definirajući određene specifikacije koje on treba zadovoljiti (vidi Definicije A2 – Specifikacije odziva u vremenskom području i s ravnini) te na temelju njih definiranja dominantnih polova prijenosne funkcije zatvorenog sustava (vidi poglavlje 5.5.1.1 Odabir željenog položaja polova zatvorenog regulacijskog sustava u kojem je dana iscrpna analiza odabira dominantnih polova vezana sa specifikacijama odziva u vremenskom i kompleksnom području). Pri tome se željeni sustav obično bira tako da nema nula i da mu pojačanje u ustaljenom stanju bude jednako 1 (GM(0)=1).
Regulator u općem slučaju ima dva ulaza - referentni signal i vođeni (izlazni) signal i jedan izlaz – upravljanje. Zakon vođenja je u z području oblika:
(5.2.5)
gdje su G CS(z) i G CP(z) impulsne prijenosne funkcije regulatora u serijskoj grani i regulatora u povratnoj grani. Regulator u serijskoj grani se obično zove serijski filter. Slika 5.1.12 prikazuje blok shemu vođenog sustava.
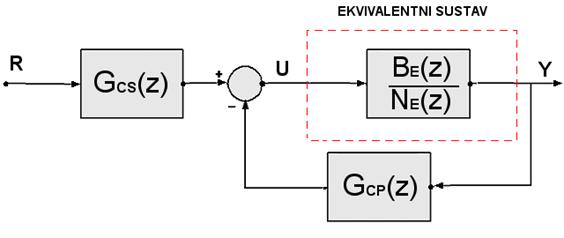
Slika
5.2.12. Regulacijska shema s dva regulatora u direktnoj i povratnoj grani
Oba regulatora također su razlomljene racionalne funkcije varijable z, i biraju se tako da im nazivnici budu isti:
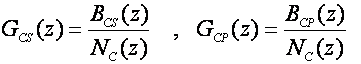(5.2.6)
Regulatori trebaju zadovoljiti i neke dodatne zahtjeve:
a) Uvjet kauzalnosti zahtijeva da red nazivnika bude veći ili jednak redu brojnika za oba regulatora. Ukoliko je red brojnika manji to znači kašnjenje signala, na primjer ukoliko je red brojnika manji za jedan od reda nazivnika, signal kroz taj regulator će kasniti jedan period uzorkovanja. Obično je to maksimalno dopušteno kašnjenje, pa je red nazivnika jednak ili najviše za jedan veći od reda brojnika impulsnih prijenosnih funkcija regulatora.
b) Zahtjev za potiskivanjem poremećaja koji se superponiraju izlaznom signalu traži da pojačanje sustava unutar povratne petlje bude veliko na niskim frekvencijama. Unutar povratne petlje imamo dvije komponente u serijskom spoju – vođeni sustav i povratni regulator
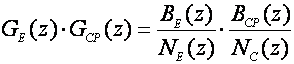(5.2.7)
Pojačanje će na niskim frekvencijama biti veliko ukoliko regulator bude integracijskog tipa, što znači da se N C(z) može napisati u obliku
(5.2.8)
U tom će slučaju vođeni sustav biti i neosjetljiv na pogreške modeliranja kontinuiranog djela koje utječu na propagaciju signala niske frekvencije. Kod nekih postupaka sinteze regulatora ovaj zahtjev nije prioritetan, pa regulatori nisu integracijskog tipa.
Uvrstimo li (5.2.6) i (5.2.5) u (5.2.3) i izračunamo prijenosnu funkciju zatvorenog sustava Y(z)/R(z) dobiti ćemo:
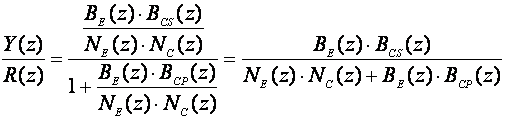(5.2.9)
Kako želimo da se zatvoreni sustav ponaša u skladu s željenom impulsnom prijenosnom funkcijom oblika (5.2.4) projektiranje regulatora se svodi na izjednačavanje (5.2.7) i (5.2.4):
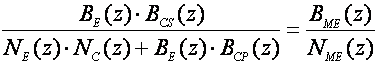(5.2.10)
i rješavanje ove algebarske jednadžbe. Rezultat su tri polinoma BCS(z), BCP(z) i NC(z) koji prema jednadžbi (5.2.6) definiraju i serijski i povratni regulator.
Općeniti je slučaj relativno složen za rješavanje i zahtjeva provjeru kauzalnosti i pojačanja na niskim frekvencijama, te čitatelje upućujemo na literaturu gdje je to detaljno objašnjeno (K.J. Åström, B. Wittenmark, Computer-controlled systems, Prentice-Hall, 1990). Rješavanje jednadžbe (5.2.10) matematički se svodi na tzv. Diophantinovu jednadžbu (Diophatin je grčki matematičar koji je živio oko 300 godine i za kojeg se smatra da je izmislio algebru) koja je oblika A X + B Y = C , gdje su A, B i C poznati polinomi, a traže se polinomi X i Y).
U nastavku ćemo se ograničiti samo na neke posebne slučajeve kod kojih je do rješenja relativno jednostavno doći. To su:
a) Čisto unaprijedno vođenje (eng. Pure Feedforward) kada nema regulatora u povratnoj grani - B CP(z) = 0. U tom slučaju iz (5.2.10) slijedi:
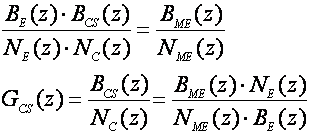(5.2.11)
Regulator se ne koristi zato što zbog nepostojanja povratne veze male pogreške u diskretnom ekvivalentu kontinuiranog dijela sustava uzrokuju lošu kvalitetu vođenja.
b) Regulator u grani pogreške (eng. Error Feedback) u stvari je standardno i uobičajeno rješenje kod kojega postoji samo jedan regulator koji se nalazi iza sumatora. To je u slučaju kada su brojnici serijskog i povratnog regulatora jednaki BCS(z) = BCP(z) = BC(z) . Iz jednadžbe (5.2.10) tada slijedi:
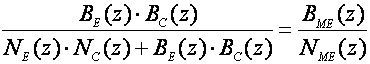(5.2.12)
iz čega računamo:
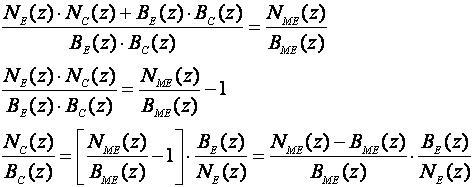(5.2.13)
pa je
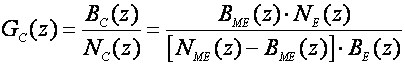(5.2.14)
Nema garancije da će sustav imati veliko pojačanje na niskim frekvencijama, a postoji mogućnost da sustav bude i nestabilan.
Napomena: Ovom je postupku vrlo sličan Dahlinov algoritam koji je bio popularan 70-ih godina. O njemu ćemo više govoriti u jednom od sljedećih poglavlja.
c) Poseban je slučaj kada su regulatori i u serijskoj i u povratnoj grani, a impulsna prijenosna funkcija vođenog sustava nema nula izvan jedinične kružnice.