5.2.2.1. Projektiranje serijsko/paralelnog regulatora kada vođeni sustav nema nestabilnih nula
Da bismo krenuli s projektiranjem regulatora potrebno je poznavati impulsnu prijenosnu ekvivalentnog sustava
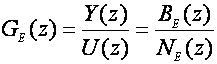
i definirati impulsnu prijenosnu funkciju željenog ponašanja zatvorenog regulacijskog sustava:
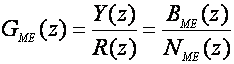
Sam postupak projektiranja sastoji se od pet koraka:
1. U serijsku se granu, poslije sumatora postavi diskretni regulator koji poništava nule ekvivalentnog vođenog sustava. Impulsna prijenosna funkcija regulatora je GC1=1/ BE(z). Situaciju prikazuje slika 5.2.13. na kojoj je ucrtan i drugi dio regulatora u povratnoj grani GC2(z) o kojem govorimo u sljedećem koraku.
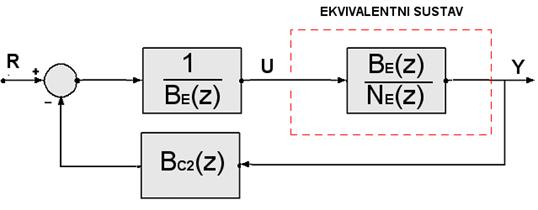
Slika 5.2.13. Regulacijska shema kod koje regulator u serijskoj grani poništava nule vođenog sustava
2. Regulator u povratnoj grani ima polinomalni oblik GC2=B C2(z). Karakteristična jednadžba sustava vođenja (nazivnik impulsne prijenosne funkcije zatvorenog sustava izjednačen s nulom) je
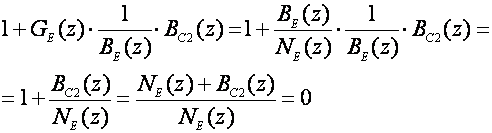
Karakteristični polinom koji definira nazivnik i polove impulsne prijenosne funkcije zatvorenog sustava jednak je brojniku ovog izraza i on glasi:
![]()
3. Ukoliko želimo da se sustav ponaša kao željeni model karakteristični polinom treba biti jednak nazivniku NME(z) željene impulsne prijenosne funkcije :
![]() (5.2.15)
(5.2.15)
iz čega slijedi polinom regulatora u povratnoj grani:
![]() (5.2.16)
(5.2.16)
4. Sada je još potrebno prebaciti sumator iza regulatora u serijskoj grani. U tom je slučaju potrebno i korigirati impulsnu prijenosnu funkciju regulatora u povratnoj grani koji postaje razlomljena racionalna funkcija
![]() (5.2.17)
(5.2.17)
Označavamo je u skladu sa slikom 5.2.2 GCP i zovemo povratni regulator. Situaciju shematski prikazuje slika 5.2.14.
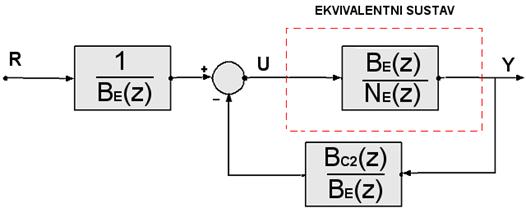
Slika 5.2.14. Modifikacija regulacijske shema prebacivanjem točke sumacije
5. Još jedino ostaje negdje ubaciti brojnik impulsne prijenosne funkcije kojom definiramo željeno ponašanja zatvorenog regulacijskog sustava. Dodajemo ga regulatoru u serijskoj grani koji sada izgleda
![]() (5.2.18)
(5.2.18)
i u skladu sa slikom 5.2.12 označava se GCS i naziva serijski regulator ili serijski filtar. Konačna shema sustava vođenja dana je na slici 5.2.15.
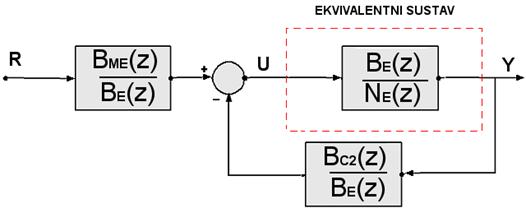
Slika 5.2.15. Konačni izgled sustava vođenja s dva regulatora, u serijskoj i povratnoj grani
Izračunamo li impulsnu prijenosnu funkciju ovako vođenog zatvorenog regulacijskog sustava dobiti ćemo:
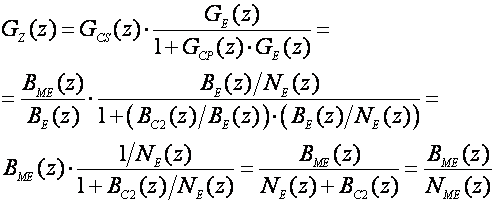
a to je upravo ono što smo i željeli.
Slika 5.2.1 prikazuje položaj sklopova za uzorkovanje koji trebaju biti i prije serijskog filtera i prije povratnog regulatora.
Primjer:
Ponovimo primjer iz prethodnog poglavlja. Istosmjerni motor ima prijenosnu funkciju:
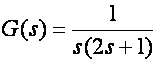
Trebamo projektirati regulator uz koji će zatvoreni sustav zadovoljiti sljedeće specifikacije: stupanj prigušenja ζ=0.65, ωp=4.77 rad/s i ωn=6.28 rad/s (M=6.8% i Tm=0.65 sek), što znači da će dominantni polovi sustava u s ravnini biti u točkama s1,2=-4.084±j4.77, odnosno u z ravnini za T=0.1 u točkama z1,2=0.591±j0.305.
Korištenje ekvivalentne impulsne prijenosne funkcije u ovom slučaju ne može dati rješenje zato što GE(z) ima nulu izvan jedinične kružnice:
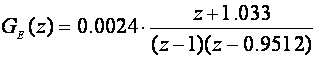
Međutim ukoliko koristimo Tustinovu aproksimaciju postupak možemo koristiti, ali zbog aproksimacijskog postupka rezultati neće biti baš potpuno točni. U proračunu ćemo koristiti i ugrađenu funkciju VisSima za pretvorbu kontinuiranog sustava u diskretni, pa se do rezultata jako brzo dođe. Pretvorba daje sljedeće vrijednosti impulsne prijenosne funkcije vođenog sustava koje odgovaraju ekvivalentnom sustavu:
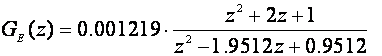
Željenu prijenosnu funkciju zatvorenog sustava određuju specifikacije: ς=0.65, ωp=4.77 rad/s i ωn=6.28:
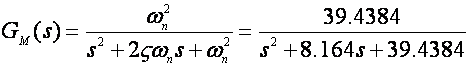
a automatska pretvorba ove prijenosne funkcije temeljena na Tustinovoj aproksimaciji je:
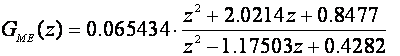
Serijski regulator (filter) ima impulsnu prijenosnu funkciju:
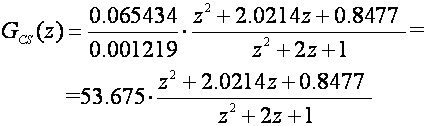
a regulator u povratnoj grani:
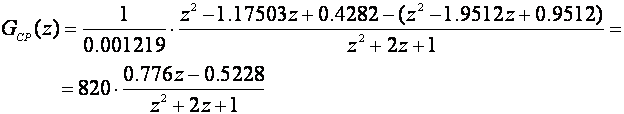
Slika 5.2.16 pokazuje odziv sustava bez vođenja i vođenog sustava.
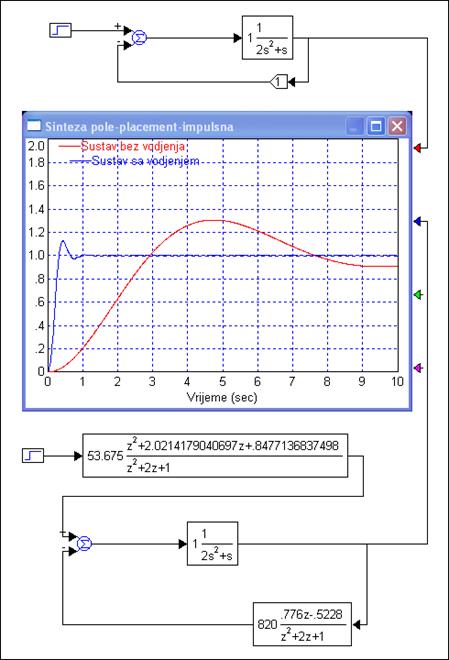
Slika 5.2.16. Odziv sustava bez vođenja i vođenog sustava kod kojeg je regulator projektiran postupkom postavljanja polova temeljen na povratnoj vezi po izlazu i projektu polinoma
Ukoliko detaljnije pogledamo dinamički dio odziva vidjeti ćemo da je odziv nešto brži i prebačaj veći. Međutim ukoliko kontinuirani dio sustava zamijenimo diskretnim ekvivalentom dobivenim aproksimacijskim postupkom, koji smo i koristili kod projektiranja regulatora, odziv se skoro u potpunosti slaže s početnim specifikacijama (M oko 7% i Tm oko 0.65 sek). Na slici 5.2.17 prikazana su oba simulirana sustava i njihovi odzivi.
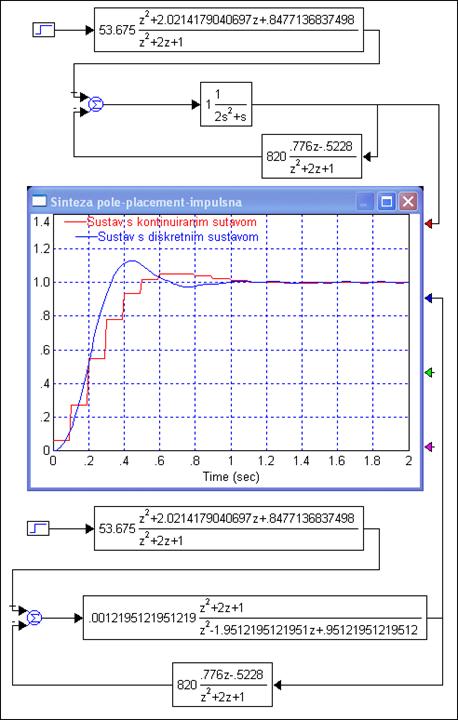
Slika 5.2.17. Odziv vođenog sustava kod kojeg je kontinuirani dio modeliran kontinuiranom prijenosnom funkcijom i diskretnim ekvivalentom dobivenim aproksimacijskim postupkom
Odzivi su u simulacijama dobri, ali pogledajmo upravljački signal. Rezultat je slika 5.2.18.
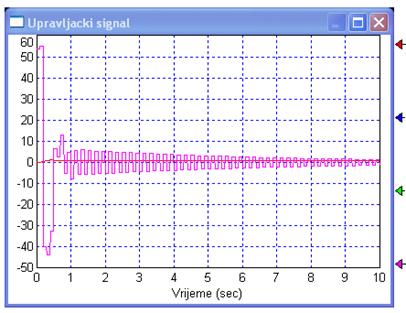
Slika 5.2.18. Upravljački signal za sustav sa slike 5.2.16
Upravljački signal u svakoj periodi alternirajući mijenja vrijednost u velikim skokovima. Niti jedan izvršni uređaj ne može pratiti ovakve zahtjeve, pa je vođenje neprimjenjivo. Pojava se zove treptanje ili zvonjenje (eng. Ringing) i uzrokuju je polovi regulatora na negativnom dijelu realne osi z kružnice. U gornjem primjeru to su dva pola u točki z = -1. Pogledamo li poglavlje o karakterističnom odzivu biti će nam jasno zašto polovi na negativnom dijelu realne z osi uzrokuju ovu pojavu. Isti se problem javio i Dahlinu, koji je još krajem 60-ih godina predložio postupak sinteze sličan gornjim postupcima, kod kojega se željeni odziv definira željenom prijenosnom funkcijom zatvorenog sustava. Kod Dahlina je razlika samo u tome što postoji samo jedan regulator i on se nalazi na uobičajenom mjestu iza sumatora. O njemu ćemo govoriti u sljedećem poglavlju, pa ćemo se u njemu dotaknuti i problema zvonjenja te opisati kako se problem razrješava.